接線方程式 -

この記事では、曲線の接線の方程式を見つける方法を説明します。さらに、さまざまな難易度の演習を解いてトレーニングすることもできます。

ある点における関数の接線の方程式

点 x=x ₀における関数 f(x) の接線の方程式は次のとおりです。

$y -y_0= m(x-x_0)$

ここで、点 P(x ₀ ,y ₀ ) は、接線と関数が一致する点です。そして、接線の傾き m は、点 x ₀における曲線の導関数、つまり m=f'(x ₀ ) に等しくなります。

上の画像では曲線が見えます

$f(x)$

青と関数に接するオレンジ色の線で表されます

$f(x)$

について

$x=x_0$

、この点しか共通点がないからです。さて、この接線の方程式は次のようになります。

$y -y_0= m(x-x_0)$

、その傾きは

$m=f'(x_0)$

。

接線方程式の求め方

ある点における関数の接線の方程式を求めるには、次の操作を行う必要があります。

接点における関数の導関数を計算して、接線の傾きを求めます。
接線上の点を決定します。
計算された傾きと接線の点を使用して接線の方程式を求めます。

曲線の接線の方程式の例

接線方程式の理論を理解したら、例を段階的に解いて接線方程式を計算する方法を見てみましょう。

曲線の接線の方程式を計算します。
$f(x)=x^2+x$

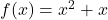
について

$x=1$

。

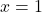
接線方程式は常に次の形式であることがわかっています。

$y -y_0= m(x-x_0)$

最初に行うことは、線の傾きを計算することです。したがって、接線の傾きは、

$m$

、接線 x=1 における曲線の導関数の値になります。つまり、

$m=f'(1).$

したがって、関数を微分してから計算します

$f'(1):$

$f(x)=x^2+x \quad \longrightarrow \quad f'(x)=2x+1$

$f'(1)= 2\cdot 1+1=2+1=3$

$m=f'(1)=3$

の価値がわかったら、

$m$

、点を見つける必要があります

$(x_0,y_0)$

接線の式を完成させます。

接線と曲線の方程式には常に共通点があり、この場合は次のようになります。

$x=1$

。したがって、曲線のように

$f(x)$

この点を通過すると、計算によって点の他の成分を見つけることができます。

$f(1):$

$f(x)=x^2+x$

$f(1)=1^2+1=2$

したがって、接点は次のとおりです。

$P(1,2)$

曲線と接線の両方がこの点を通過するため、これを使用して接線の方程式を見つけることもできます。

残っているのは、見つかった傾きと接線の値を方程式に代入することだけです。

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=3 \qquad P(1,2) \end{array} \right\} \longrightarrow \ y -2= 3(x-1)$

つまり、接線方程式は次のようになります。

$\bm{y-2=3(x-1)}$

接線の方程式を明示的な線の方程式で表すこともできます。

$\bm{y=3x-1}$

以下に曲線を示します。

$f(x)=x^2+x$

とその接線

$x=1,$

$y-2=3(x-1):$

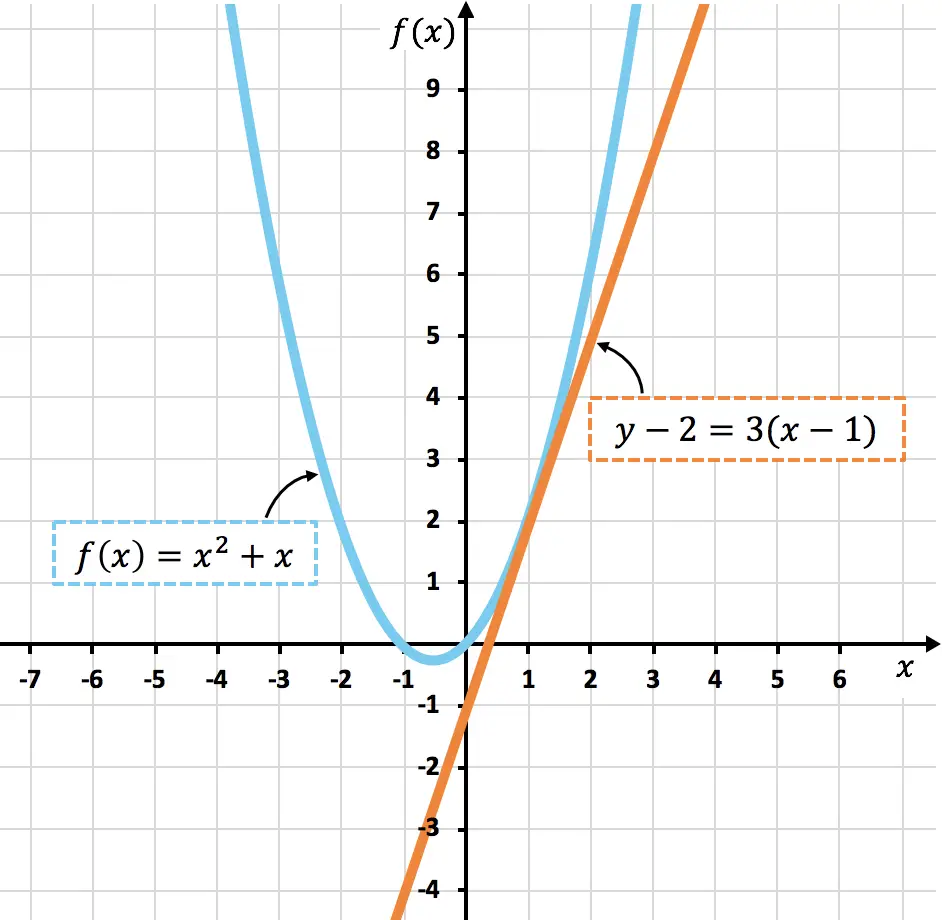
ご覧のとおり、曲線です

$f(x)=x^2+x$

そしてタンジェント

$y-2=3(x-1)$

彼らには共通点があるだけだ

$(1,2)$

、計算どおりです。

正接方程式の演習問題を解決しました

演習 1

曲線の接線の方程式を計算します。

$f(x)=2x^2-4x+3$

について

$x=2 .$

解決策を見る

接線方程式は常に次の形式になります。

$y-y_0=m(x-x_0)$

ステップ 1: 接線の傾きを計算する

傾きmは、曲線の接点における導関数の値です。したがって、この場合、

$m = f'(2):$

$f(x)=2x^2-4x+3 \ \longrightarrow \ f'(x)= 4x-4$

$f'(2)= 4\cdot 2-4=8-4=4$

$m=f'(2)=4$

ステップ 2: 接線上の点を見つける

接線と曲線の方程式には常に共通点があり、この場合は次のようになります。

$x=2$

。したがって、曲線のように

$f(x)$

この点を通過すると、計算によって点の他の成分を見つけることができます。

$f(2):$

$f(x)=2x^2-4x+3$

$f(2)=2\cdot 2^2-4\cdot 2+3 =2 \cdot 4 -8 +3 = 3$

したがって、曲線と接線の両方が通過する点が点になります。

$(2,3).$

ステップ 3: 接線方程式を書く

残っているのは、見つかった傾きと接線の値を方程式に代入することだけです。

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=4 \qquad P(2,3) \end{array} \right\} \longrightarrow \ y -3= 4(x-2)$

したがって、接線方程式は次のようになります。

$\bm{y -3= 4(x-2)}$

演習 2

曲線の接線の方程式を計算します。

$\displaystyle f(x)=-3x^2+2x$

座標の原点にあります。

解決策を見る

座標の原点は点を指します

$(0,0).$

したがって、次の点での関数の接線を計算する必要があります。

$(0,0) .$

まず、座標の原点で導関数を計算して、接線の傾きの値を決定します。

$f(x)=-3x^2+2x \ \longrightarrow \ f'(x)= -6x+2$

$f'(0)= -6\cdot 0+2=2$

$m=f'(0)=2$

この場合、接線が通過する点はすでにわかっています。このステートメントは、直線が座標の原点、つまり点で曲線に接している必要があることを示しているためです。

$(0,0).$

したがって、曲線と接線が共有する点が点です

$(0,0).$

最後に、見つかった傾きと接線の値を方程式に代入するだけです。

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=2 \qquad P(0,0) \end{array} \right\} \longrightarrow \ y -0= 2(x-0)$

結論として、接線方程式は次のようになります。

$y -0= 2(x-0)$

$\bm{y = 2x}$

演習 3

曲線の接線を計算します

$f(x)=x^2-2x-1$

右に平行なものは

$y-4x-6=0$

。

解決策を見る

この問題では、接線は直線に平行でなければならないと言われています。

$y-4x-6=0 .$

そして、2 本の直線の傾きが同じであれば平行です。したがって、接線は直線と同じ傾きを持つ必要があります。

$y-4x-6=0.$

これは、線の傾きを見つける必要があることを意味します

$y-4x-6=0 .$

これを行うには、変数をクリアして次のようにします。

$y-4x-6=0 \ \longrightarrow \ y =4x+6$

したがって、線の傾きは

$y=4x+5$

y が明確な場合、線の傾きは x を乗算する数値であるため、は 4 になります。

したがって、接線の傾きも 4 でなければなりません。接線が平行であるためには、同じ傾きを持つ必要があるからです。

$m=4$

この場合、曲線と接線の間の接点はわかりません。しかし、曲線の接点における導関数は接線の傾きに等しいことがわかっています。

$m=f'(x_0)$

。さて、どうやってその価値を知ることができるのでしょうか？

$m$

、方程式から x ₀を見つけることができます。

$m=f'(x_0):$

これを行うには、まず次の導関数を計算します。

$f(x):$

$f(x)= x^2-2x-1 \ \longrightarrow \ f'(x)=2x-2$

そして今、私たちは解決します

$m=f'(x_0)$

知っています

$m = 4 :$

$m =f'(x_0)$

$4 =2(x_0)-2$

$4+2 =2x_0$

$6 =2x_0$

$\cfrac{6}{2} =x_0$

$3=x_0$

点の x 座標がわかったら、次の計算によって点の他の座標を見つけることができます。

$f(3):$

$f(3)=3^2-2\cdot 3-1= 9-6-1=2$

したがって、曲線と接線の両方が通過する点が点になります。

$(3,2).$

残っているのは、見つかった傾きと接線の値を方程式に代入することだけです。

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=4 \qquad P(3,2) \end{array} \right\} \longrightarrow \ y -2= 4(x-3)$

そして、接線の方程式は次のようになります。

$\bm{y -2=4(x-3)}$

演習 4

曲線の接線を計算します

$f(x)=2x^2+5x+1$

X 軸と 45 度の角度を形成します。

解決策を見る

問題文は、接線が X 軸に対して 45 度の角度を形成する必要があることを示しています。このような場合、次の式を適用して傾きの値を求める必要があります。

$m = \text{tg}\left(\alpha\right)$

$m = \text{tg}\left(45^{\text{o}}\right) = 1$

このステートメントでは、曲線と接線の間の接点が指定されていません。しかし、接線点における曲線の導関数は接線の傾きに等しいことがわかっています。

$m=f'(x_0)$

。したがって、方程式を解くことで x ₀を計算できます。

$m=f'(x_0):$

これを行うには、まず次の導関数を計算します。

$f(x):$

$f(x)=2x^2+5x+1\ \longrightarrow \ f'(x)=4x+5$

そして今、私たちは解決します

$m=f'(x_0)$

知っています

$m = 1 :$

$m =f'(x_0)$

$1 =4(x_0)+5$

$1-5 =4x_0$

$-4 =4x_0$

$\cfrac{-4}{4} =x_0$

$-1=x_0$

点の x 座標がわかったら、次の計算によって点の他の座標を見つけることができます。

$f(-1):$

$f(-1)=2(-1)^2+5(-1)+1=2\cdot 1 -5 + 1 = -2$

したがって、曲線と接線の両方が通過する点が点になります。

$(-1,-2).$

残っているのは、見つかった傾きと接線の値を方程式に代入することだけです。

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=1 \qquad P(-1,-2) \end{array} \right\} \longrightarrow \ y -(-2)= 1(x-(-1))$

最後に、接線の方程式を求める操作を実行します。

$y -(-2)=1(x-(-1))$

$y +2=1(x+1)$

$\bm{y + 2=x+1}$

ある点における関数の接線の方程式

接線方程式の求め方

曲線の接線の方程式の例

正接方程式の演習問題を解決しました

演習 1

演習 2

演習 3

演習 4

コメントする 返信をキャンセル

コメントする返信をキャンセル