ここでは、恒等関数とは何かを説明します。さらに、恒等関数をグラフィカルに表現する方法とその特性を理解できるようになります。
恒等関数とは何ですか?
恒等関数とは、引数と同じ値をイメージとして持つ関数です。恒等関数はid という用語で表現できます。
したがって、恒等関数の数式は次のようになります。
![]()
たとえば、x=1 の恒等関数の画像は 1 の価値があり、x=2 の画像は 2 の価値があり、x=3 の画像は 3 の価値があります。
![Rendered by QuickLaTeX.com \begin{array}{c}f(1)=1\\[2ex]f(2)=2\\[2ex]f(3)=3\\ \bm{\vdots}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4b85e48e3f36d1eb4271b265aaf35bef_l3.png)
恒等関数は線形関数の一例です。次のリンクでは、このタイプの関数の例をさらに見ることができます。
➤参照: 一次関数の例
恒等関数のグラフ表示
恒等関数のグラフは、第 1 象限と第 3 象限の二等分線である線に対応します。
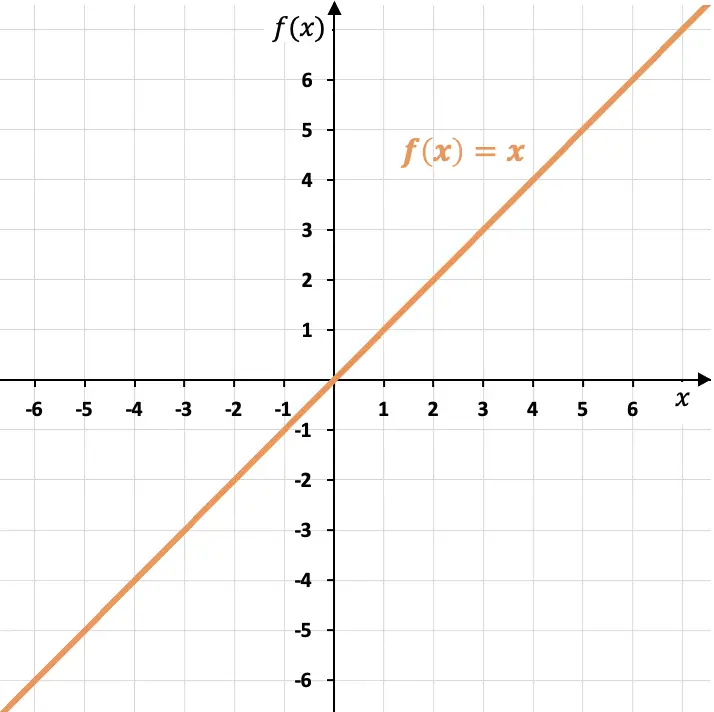
ご覧のとおり、恒等関数は座標の原点 (点 (0,0)) を通過し、変数の 1 単位が増加し、独立した値ごとに 1 に等しい傾き (m=1) を持ちます。さらに、恒等関数は X 軸に対して 45 度の角度を形成します。
恒等関数の特徴
恒等関数には次のプロパティがあります。
- 恒等関数の定義域はすべて実数です。
![]()
- 恒等関数の範囲 (または範囲) もすべての実数で構成されます。
![]()
- 恒等関数は連続かつ全単射関数です。
- また、恒等関数は奇関数で構成されており、座標の原点に対して対称な関数となっています。
![]()
➤ 「奇数対称関数」を参照
- 恒等関数はドメイン全体で増加しており、その傾きは 1 に等しくなります。
![]()
- x 軸 (OX 軸) と y 軸 (Y 軸) が同じ点、つまり座標原点で交差します。
![]()
- これは、1 次多項式関数として分類できます。
- 恒等関数は、 関数合成の中立的な要素として機能します。そのため、恒等関数で構成される関数は関数自体になります。
![]()
- 値
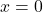
は、このタイプの関数の唯一のルートです。
- x がプラスの無限大またはマイナスの無限大に向かう傾向がある場合の恒等関数の極限は、それぞれプラスの無限大とマイナスの無限大を与えます。
![]()
![]()
- したがって、恒等関数には漸近線がありません。
- 恒等関数の導関数は、値 1 の定数関数です。
![]()
- 恒等関数の積分は二次関数です。
![]()
➤参照:2 次関数の公式