このページでは、対角行列とは何か、および対角行列の例を示します。さらに、このタイプの行列を操作する方法、行列式を簡単に計算する方法、および行列式を逆にする方法も学びます。対角行列のプロパティと応用もあります。最後に、2 重対角行列と 3 重対角行列について説明します。
対角行列とは何ですか?
対角行列は、主対角線上にないすべての要素がゼロ (0) である正方行列です。主対角線の要素はゼロである場合もあれば、ゼロでない場合もあります。
対角行列の正確な定義がわかったら、対角行列の例を見ていきます。
対角行列の例
2 × 2 次元の対角行列の例
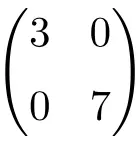
3×3次の対角行列の例

サイズ 4×4 の対角行列の例
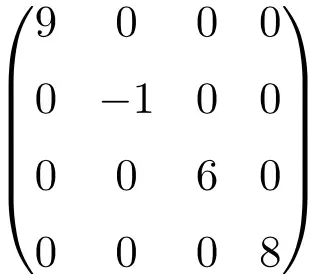
これらのタイプの行列は通常、対角要素を示して記述されます。
![Rendered by QuickLaTeX.com diag(2,5,1) = \left. \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 5 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-14216c3a6fd6e7bfd4c9d78ac2a4765c_l3.png)
対角行列を使用した演算
対角行列が線形代数にとって非常に重要である理由の 1 つは、対角行列を使用すると計算が容易になるためです。これが、それらが数学で非常に使用される理由です。
対角行列の加算と減算
2 つの対角行列の加算 (および減算) は非常に簡単です。対角線上の数値を加算 (または減算) するだけです。
![]()
例えば:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & -2 & 0 \\[1.1ex] 0 & 0 & 6 \end{pmatrix} +\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & -4 \end{pmatrix} = \begin{pmatrix} 6& 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e659649fca7fe55f33c0f3452e8c46f2_l3.png)
対角行列の乗算
2 つの対角行列の乗算または行列積を解くには、単純に対角要素を掛け合わせます。
![]()
例えば:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & -4 & 0 \\[1.1ex] 0 & 0 & -3 \end{pmatrix} \cdot\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & -2 & 0 \\[1.1ex] 0 & 0 & 6 \end{pmatrix} = \begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & -18 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0bcb4a59778cc41eed67dce0bc384682_l3.png)
対角行列の力
対角行列のべき乗を計算するには、対角行列の各要素を指数化する必要があります。
![]()
![]()
例えば:
![Rendered by QuickLaTeX.com \displaystyle\left. \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix}\right.^3= \begin{pmatrix} 27 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & 64 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4d27337283f4b6029bff166fb8e3458d_l3.png)
対角行列の行列式
対角行列の行列式は、主対角要素の積です。
![]()
![]()
次の解決済み演習を見てください。この演習では、主対角要素を乗算するだけで対角行列の行列式を求めます。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 3 \end{vmatrix} = 5 \cdot 2 \cdot 3 = 30](https://mathority.org/wp-content/ql-cache/quicklatex.com-f34514c6e1559b8ebb296ee6c51a33d6_l3.png)
この定理は証明するのが簡単です。必要なのは、ブロック (または余因子) による対角行列の行列式を計算することだけです。このデモンストレーションは、一般的な対角行列を使用して以下で詳しく説明されます。
![Rendered by QuickLaTeX.com \begin{aligned} \begin{vmatrix} a & 0 & 0 \\[1.1ex] 0 & b & 0 \\[1.1ex] 0 & 0 & c \end{vmatrix}& = a \cdot \begin{vmatrix} b & 0 \\[1.1ex] 0 & c \end{vmatrix} - 0 \cdot \begin{vmatrix} 0 & 0 \\[1.1ex] 0 & c \end{vmatrix} + 0 \cdot \begin{vmatrix} 0 & b \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (b\cdot c) - 0 \cdot 0 + 0 \cdot 0 \\[2ex] & = a \cdot b \cdot c \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7b8718172b4b70d1ccacb01ea7ed5dd4_l3.png)
対角行列を逆にする
対角行列は、主対角のすべての要素が 0 とは異なる場合にのみ反転可能です。この場合、対角行列は正則行列と言います。
さらに、対角行列の逆行列は、常に主対角行列の逆行列を持つ別の対角行列になります。
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 8 \end{pmatrix} \ \longrightarrow \ A^{-1}=\begin{pmatrix} \frac{1}{3} & 0 & 0 \\[1.1ex] 0 & \frac{1}{2} & 0 \\[1.1ex] 0 & 0 & \frac{1}{8} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a91beaaca82477a0c882b42da4eb7481_l3.png)
前の特性から、対角行列の逆行列の行列式は主対角行列の逆行列の積であると推測できます。
![Rendered by QuickLaTeX.com \displaystyle B= \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 4 & 0 \\[1.1ex] 0 & 0 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0571390802f955fac935aeb9cf4ab92f_l3.png)
![]()
対角行列のプロパティ
- 対角行列はすべて対称行列でもあります。
- 対角行列は、上三角と下三角の両方を持つ行列です。
- 単位行列は対角行列です。
![Rendered by QuickLaTeX.com \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e4e9931fb7ae104414006cee93978a7_l3.png)
- 同様に、ゼロ行列も対角線上にない要素はすべてゼロであるため、対角行列です。対角線の数字は0ですが。
![Rendered by QuickLaTeX.com \begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-edb061dcbc869eba51ece12af43f796f_l3.png)
- 対角行列の固有値 (または固有値) は、その主対角要素です。
![Rendered by QuickLaTeX.com \begin{pmatrix} 7 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix} \longrightarrow \ \lambda = 3 \ ; \ \lambda = 4 \ ; \ \lambda = 7](https://mathority.org/wp-content/ql-cache/quicklatex.com-1dea3de2ae28d46194ead012bc001cf0_l3.png)
- 正方行列は、三角形で法線である場合にのみ対角になります。
- 対角行列の随伴物は別の対角行列です。
対角行列のアプリケーション
これまで見てきたように、演算には多くのゼロが含まれるため、対角行列を使用した計算を解くことは非常に簡単です。このため、数学の分野で非常に役立ち、広く使用されています。
これと同じ理由で、行列を対角化する方法について非常に多くの研究が行われ、実際に行列を対角化する方法 (特性多項式を使用した) も開発されました。
したがって、対角化可能な行列も非常に関連性があります。スペクトル分解定理と同様に、行列を対角化できる場合とできない場合の条件を確立します。
二重対角行列
二重対角行列は、主対角線上または上下の対角線上にないすべての要素が 0 である正方行列です。
例えば:
![Rendered by QuickLaTeX.com \begin{pmatrix} 3 & 2 & 0 \\[1.1ex] 0 & -5 & 1 \\[1.1ex] 0 & 0 & 6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d9acdfc09d0167548ef3f6f5b58d9276_l3.png)
上二重対角行列
![Rendered by QuickLaTeX.com \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 6 & 2 & 0 \\[1.1ex] 0 & 7 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b2b53f238add73431696006f4b05a2d8_l3.png)
下側二重対角行列
主対角線と最初の上対角線が占有されている場合、上二重対角行列と呼ばれます。一方、主対角線と最初の下対角線が占有されている場合、下側二重対角行列と呼ばれます。
三重対角行列
三重対角行列は、主対角要素と上下の隣接する対角要素のみが非ゼロ要素である正方行列です。
例えば:
![Rendered by QuickLaTeX.com \begin{pmatrix} 2 & 3 & 0 & 0 \\[1.1ex] -4 & 5 & 9 & 0 \\[1.1ex] 0 & 1 & 6 & -2 \\[1.1ex] 0 & 0 & 8 & 7 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9a8fbe0404c447268a89ff954e3b23d5_l3.png)
したがって、すべての対角行列、2 重対角行列、および 3 重対角行列はバンド行列の例です。なぜなら、バンド行列は主対角線の周りにすべての非ゼロ要素を持つ行列だからです。