このページでは、対称行列とは何かについて説明します。さらに、行列が対称であるかどうかを簡単に特定する方法と、いくつかの例を示しているので、迷うことはありません。対称行列のすべてのプロパティも見つかります。最後に、正方行列が持つ特定の特徴を説明します。それは、対称行列と非対称行列の和に分解できるということです。
対称行列とは何ですか?
対称行列の定義は次のとおりです。
対称行列は、転置が行列自体と等しい正方行列です。
![]()
金
![]()
の転置行列を表します
![]()
。
対称行列の概念を理解すると、対称行列がどのように簡単に識別できるかがわかります。
行列が対称になるのはどのような場合ですか?
対称行列の構造を認識するのは非常に簡単です。行iおよび列jの要素は、行jおよび列iの要素と同一でなければなりません。そして、行列の主対角の値は任意です。
対称行列の例
理解を助けるために、対称行列の例をいくつか示します。
2 × 2 次の対称行列の例
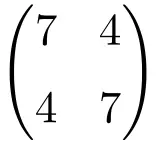
次元 3×3 の対称行列の例

サイズ 4×4 の対称行列の例
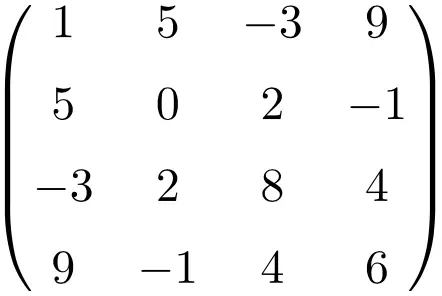
これら 3 つの行列を転置することにより、転置された行列はそれぞれの元の行列と同等であるため、それらが対称であることを確認します。
なぜ対称行列と呼ばれるのでしょうか?
前の例をよく見ると、対称行列の主対角線は対称軸です。つまり、対角線の上の数値と下の数値の間の鏡として機能します。このため、これらのタイプの行列は対称と呼ばれます。
対称行列の性質
対称行列の特徴は次のとおりです。
- 2 つの対称行列を加算 (または減算) すると、別の対称行列が得られます。 2 つの加算 (または減算) 行列を転置することは、各行列を個別に転置することと同じであるため、次のようになります。
![]()
- 対称行列にスカラーを乗算すると、別の対称行列が生成されます。
- 同様に、2 つの対称行列間の行列積は、2 つの行列が交換できる場合に限り、別の対称行列と常に等しいとは限りません。この条件は、転置行列の乗算プロパティで証明できます。
![]()
- 指数が整数である限り、対称行列の累乗により別の対称行列が生成されます。
- 明らかに、ユニタリ行列とゼロ行列は対称行列の例です。
- 対称行列に合同な行列も対称でなければなりません。
- 対称行列が正則または可逆行列であれば、その逆行列も対称です。
- 対称行列の随伴行列も同様です。対称行列の随伴行列は、解として別の対称行列を与えます。
- 真の対称行列は正規行列でもあります。
- 対称行列はエルミート行列の特殊なケースであるため、対称行列のすべての固有値 (または固有値) は実数です。
- スペクトル定理は、要素が実数であるすべての行列は対角化可能な行列であり、さらに、対角化は直交行列によって実行されることを示しています。したがって、すべての実対称行列は直交対角化されます。
- 一方、複素数の対称行列はユニタリ行列によって対角化できます。
- ヘッセ行列は常に対称です。
正方行列の対称行列と非対称行列への分解
正方行列の特別な特徴は、対称行列と非対称行列の和に分解できることです。
これを可能にする式は次のとおりです。
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} C = S + A \\[2ex] S = \cfrac{1}{2}\cdot (C+C^t) \qquad A = \cfrac{1}{2} \cdot (C-C^t)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a3b9aa2b7ed0e9ce31587d4f00f1144e_l3.png)
ここで、C は分解したい正方行列、Cはその転置行列、最後に S と A はそれぞれ行列 C が分解される対称行列と非対称行列です。
以下に、これがどのように行われるかを確認するための解決済み演習を示します。次の行列を分解してみましょう。
![Rendered by QuickLaTeX.com \displaystyle C=\begin{pmatrix} 2& -1 \\[1.1ex] 3 &0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-852a7267895a7f332ad3f28f8a8dda0d_l3.png)
次の式を使用して対称行列と非対称行列を計算します。
![Rendered by QuickLaTeX.com \displaystyle S=\cfrac{1}{2}\cdot (C+C^t)= \begin{pmatrix} 2& 1 \\[1.1ex] 1 &0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-994670ecc17b3bc8757482f1656e543e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A=\cfrac{1}{2}\cdot (C-C^t)= \begin{pmatrix} 0& -2 \\[1.1ex] 2 &0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d87e1d30d2bc657c20535f45c0fb7be6_l3.png)
そして、2 つの行列を加算することで方程式が満たされていることを確認できます。
![]()
![Rendered by QuickLaTeX.com \displaystyle\begin{pmatrix} 2& 1 \\[1.1ex] 1 &0\end{pmatrix}+\begin{pmatrix} 0& -2 \\[1.1ex] 2 &0\end{pmatrix}=\begin{pmatrix} 2& -1 \\[1.1ex] 3 &0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7cfdbffec6801c13041cd2996da13e96_l3.png)
![]()
✅