多項式関数 - Mathority

この記事では、多項式関数についての非常に詳細な説明があり、例によって補足されています。さらに、最後に紹介する演習を通じて、多項式関数が日常生活でどのように使用されるかを理解できるようになります。

多項式関数とは何ですか?

多項式関数または多項式関数は、多項式と同等の代数式によって与えられる関数です。これは、式が多項式の構造に従わなければならないことを意味します: f(x) = a ₀ + a ₁ x + a ₂ x ² + a ₃ x ³ + … + a _n x ⁿ (どの構造に依存するか)処理する多項式関数のタイプを決定します。これらの関数のもう 1 つの非常に重要な特徴は、未知数の指数がすべて正の整数であることです。

多項式関数の一部

これらの機能に関する 3 つの重要な要素を強調できます。

多項式係数:これらは未知数に付随する数値です。たとえば、次の項の 3 は係数です: 3x ² 。多項式の項と同じ数の係数があることに注意してください。
多項式の指数または指数:これらは未知数の累乗です。たとえば、次の項の 2 は指数です: 3x ² 。すでに説明したように、多項式関数の場合、それらは常に正の整数になります。
多項式の次数:この値は、多項式を構成するすべての項の中で最も高い次数の指数に相当します。多項式 f(x) = 3x ² – 4x + 2 の場合、次数は 2 に等しくなります。

関数が多項式かどうかはどうやってわかりますか?

多項式関数を特定するには、それが今説明した特性を満たしているかどうかを確認する必要があります。まず、関数を定義する式が多項式構造であるかどうかを確認します: f(x) = a ₀ + a ₁ x + a ₂ x ² + a ₃ x ³ + … + a _n x ⁿ 。次に、インデックスが正の整数であることを確認します。これらの簡単な手順で、関数が多項式かどうかを判断できます。

多項式関数の種類と例

次に、多項式の次数に応じて分類された、存在するさまざまな種類の多項式関数を示します。さらに、各タイプのグラフィック表現の例も見つかります。これらの多項式関数の例のおかげで、さまざまなカテゴリ間の違いをよりよく理解できるようになります。

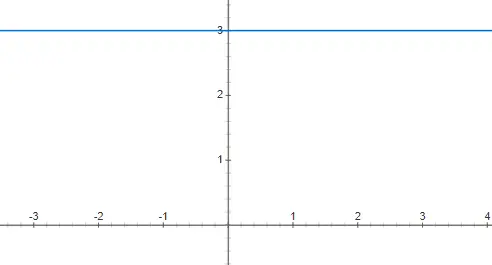
定数関数

定数関数は次数 0 の多項式と等価です。これは、x の係数が 0 であることを意味します。これが、このタイプの関数が独立変数 x の値に依存しない理由です。したがって、そのグラフィック表現は無限の水平線になります。以下に f(x) = 3 の例を示します。

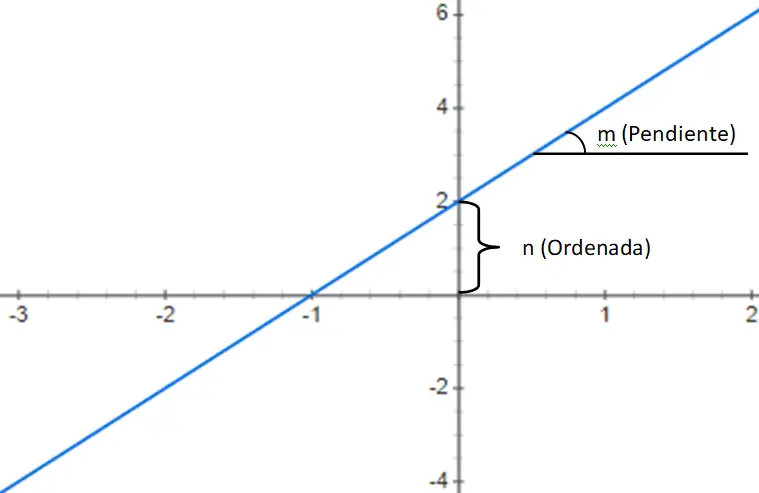
一次多項式関数

次に、次の構造を持つ 1 次多項式によって与えられる 1 次多項式関数を求めます: f(x) = mx + n。この式は、変数 xy に定数 (n) を乗算し、この積に加算する傾き (m) と呼ばれる数値で構成されます。したがって、m と n の値に基づいて、3 つの異なるタイプの関数を識別できます。

アフィン関数:このサブタイプは、n の値が 0 とは異なる、つまりコンピューターの値が 0 とは異なるという特徴があります。したがって、このタイプの関数は点 (0, 0) を通過しません。起源。また、m < 0 の場合、関数は減少し、m > 0 の場合、関数は増加することもコメントします。
線形関数:これらの関数とアフィン関数の唯一の違いは、n = 0 であるため、コンピューターを持たないことです。したがって、一次関数の式は f(x) = mx と等価です。このタイプは常に点 (0, 0) を通過し、傾きからすでにグラフが得られているため、非常に簡単に表現できます。
恒等関数:この最後のタイプは、線形関数のサブグループで、an = 0 および m = 1 です。これは、式が f(x) = x のままであることを意味し、グラフ表現は、次の関数と 45 度の角度を形成する対角線になります。軸の一つ。このタイプの関数も原点 (0, 0) を通過します。

以下に、1 次多項式関数、より正確にはアフィン関数 f(x) = 3x + 2 の例を示します。

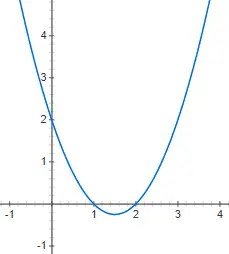
二次関数

2 次関数または2 次関数は、f(x) = ax ² + bx + c の構造に従う 2 次多項式を使用して表現されます。ここで、a は 0 とは異なります。この場合、グラフィック表現はより複雑になります。もはや直線ではなく、垂直な放物線です。以下に、二次関数 f(x) = 2x ² + 4x – 1 の表現を示します。

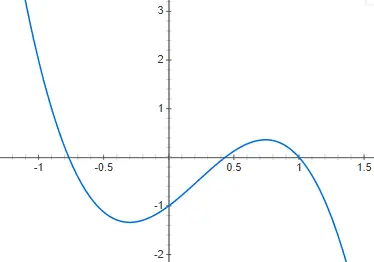
3次関数

3 次関数または 3 次の関数は、 3次の多項式 f(x) = ax ³ + bx ² + cx + d で与えられ、0 とは異なります。このスタイルの関数の表現は、次の関数よりもさらに複雑です。いくつかの異なる形式がある可能性があるため、第 2 級のものです。基本的な形式、または少なくとも最も一般的な形式は、次の例で示す f(x) = 2x ³ – 4x ² + 2x – 2 です。

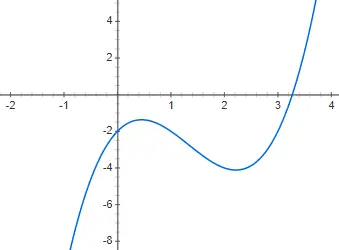
多項式関数の性質

多項式関数には、他の関数とは異なる一連のプロパティや特性があり、以下でできるだけ明確に説明します。こうすることで、次のような関数が表示されたときに、それらを識別するのが非常に簡単になります。

多項式関数の定義域はすべての実数(Dom f = R または Dom f = (-∞, ∞)) に等しいため、実数のセット全体にわたって連続です。
Y 軸上のその交点は (0, a ₀ ) に相当し、 ₀は独立項です。
多項式の次数以下の回数、X 軸に沿ってカットします。
多項式関数には漸近線がありません。
すべての項の指数が奇数の場合、グラフは座標原点に関して対称になります。一方、すべての項の指数が偶数の場合、グラフは OY 軸に関して対称になります。
この形式の関数の変曲点の数は、n – 2 以下になります (n は次数)。
このスタイルの関数の相対最大値と相対最小値の数は、n – 1 以下になります (n は次数)。

多項式関数をどのように解析しますか?

多項式関数を解析するには、他の関数を解析する場合と同じ手順に従う必要があります。次のリストには、調査または治療する必要があるさまざまな要素がまとめられています。

ドメインと範囲
横軸と縦軸との交点
単調性（増加と減少、最大値と最小値）
曲率 (1 より大きい次数の関数)

もちろん、分析を別のレベルに引き上げて、他の多くの要素を研究することもできますが、これだけでも十分です。これらの要素を理解すると、関数がどのようなものかを明確に把握でき、それをグラフィカルに表現できるようになります。

多項式関数の演習

次に、関数、特に多項式関数を表現する練習をするための一連の演習を提供します。このようにして、この記事で説明したすべての概念を統合します。

演習 1

次の 1 次多項式関数 f(x) = x + 2 をグラフにして、それがどのような型であるかを言います。

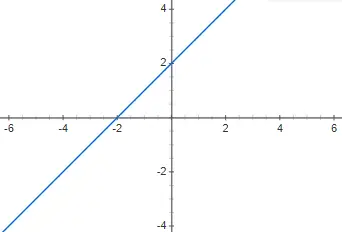
これは 0 とは異なり、m も 0 とは異なるため、1 次のアフィン多項式関数です。

演習 2

次の 2 次多項式関数 f(x) = x ² + x – 2 をグラフにします。

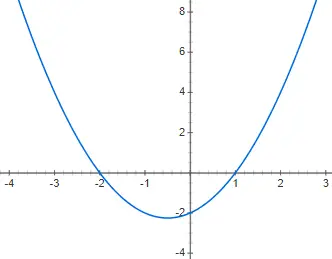
演習 3

次の 3 次多項式関数 f(x) = x ² + x – 2 をグラフにします。