このページでは、多項式の独立項とは何か、またその計算方法について説明します。さらに、さまざまな多項式の独立項を識別する方法に関するいくつかの例が表示され、解決された演習で練習することもできます。
多項式の独立項とは何ですか?
多項式の独立項の定義は次のとおりです。
数学では、多項式の独立項は変数を持たない項です。したがって、多項式の独立項は、多項式の 0 次の単項に対応します。
たとえば、次の多項式の独立項は 7 です。
![]()
前の例の多項式では、リテラル部分を持たない項、つまり x を持たない項は数値 7 です。このため、この多項式の独立項は 7 になります。
多項式の独立項は非常に単純な概念のように見えますが、一部の多項式の計算には非常に役立つことを知ってください。たとえば、 多項式の根を求める手順は、その独立項から始まります。多項式の根 (またはゼロ) を見つける方法について詳しく知りたい場合は、このリンクをチェックしてください。ここでは例も表示され、段階的に解決される演習で練習することができます。
多項式の独立項の例
多項式の独立項の意味を理解したら、多項式の独立項を見つける方法の例をいくつか見ていきます。
- 4 次の多項式の独立項の例:
![]()
この例の多項式はモニック多項式であり、変数を持たない項は 5 であるため、多項式の独立項の値は 5 になります。
- 5 次の多項式の独立項の例:
![]()
変数 x を伴わないこの多項式の要素は -2 であるため、多項式の独立項になります。数値の負の符号も独立項に含まれることに注意してください。
- 8 次の多項式の独立項の例:
![]()
この多項式のすべての単項式は +1 を除く変数を持つため、多項式の独立項は +1 になります。
最後に、独立項の特性の 1 つは、x=0 の多項式の数値が常にその独立項と等しいことです。この奇妙なことにもっと興味がある場合は、リンク先のページで多項式の数値がどのように計算されるかを調べることができます。さらに、これがどのように行われるかの例もいくつかあり、演習を解いて練習することもできます。一歩ずつ。
多項式の独立項に関する演習を解決しました
多項式の独立項が何であるかを理解するには、以下で解く演習を行うことをお勧めします。
- 多項式を考えると
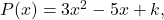
独立項の値を計算します

それが満たされるように
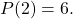
この問題を解決するために最初に行うことは、次のことを判断することです。
![]()
まだ:
![]()
パワーを計算します。
![]()
乗算を行います。
![]()
そして項として減算します。
![]()
したがって、ステートメントの条件が満たされるためには、得られた代数式を 6 に等しくする必要があります。
![]()
![]()
したがって、結果として得られる方程式を解くだけで十分です。
![]()
![]()
結論として、多項式の独立項は 4 でなければなりません。
最後に、ルフィニの法則を正しく適用するには、多項式の独立項も重要であることを知っておく必要があります。それが何であるかわからない場合のために説明すると、ルフィニの法則は、多項式をすばやく除算するために使用される方法です。ここでは、 ルフィニの法則の実行方法と、それが多項式の独立項にどのように関連するかを確認できます。