多項式 - マソロリティ

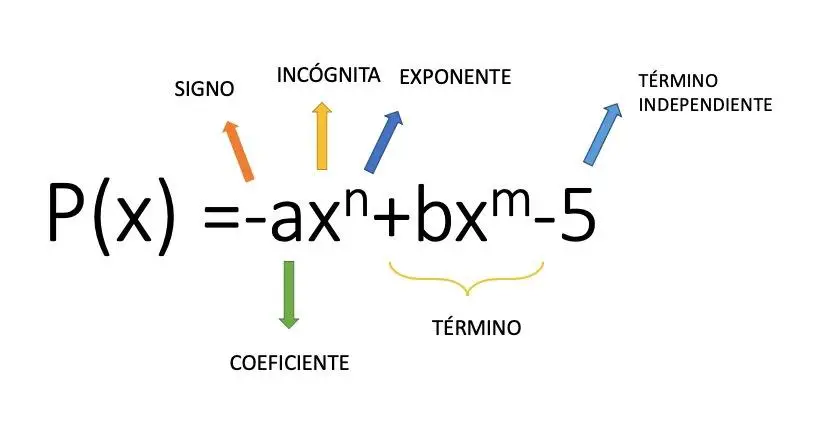
単項式は、変数に指数を乗算する係数 (数値) によって形成される代数式です。たとえば、式 4x² は単項式です。したがって、この数学的概念から、いくつかの単項式の加算と減算のセットである多項式に到達します。上の画像では、複数の単項式で構成される多項式の構造の例を示しています。

多項式の種類

特定の単項式の指数を通じて、多項式をさまざまなタイプに分類できます。これらの式は、1 次多項式、2 次多項式、3 次多項式などのカテゴリに分類できます。基本的に、最大の指数を持ち、多項式の次数となる単項式を特定する必要があります。それが分かれば、今お話ししたタイプのいずれかに分類することができます。

複数の変数の多項式

さらに、多項式を構成する単項式の数に応じて多項式を編成する別の方法もあります。たとえば、 binomialがある場合、これは 2 つの項を含む多項式を持つことと同等になり、 trinomialがある場合、これは 3 つの項を含む多項式を持つことと同等になります。多項式をカタログ化するこれらの方法にはすべて、無限に多くのサブカテゴリがあります。これらの式は任意の単項式で構成でき、任意の次数を持つこともできるためです。

多項式の特徴と性質

多項式の絶対次数:前のセクションでは、相対次数の定義について説明しました。しかし、複数の変数で形成される多項式の場合、この単項式のすべての変数の指数の最大合計に等しい絶対次数が得られます。たとえば、単項式 5x²y³ では、絶対次数は 2 + 3 = 5 に等しくなります。
順序多項式:変数の指数が昇順または降順に配置されている場合、その変数に関して順序多項式を定義します。たとえば、この多項式 P(x) = 3x + 4x³ – x² が見つかった場合、この場合は順序付けされません。したがって、これを修正すると、次の結果が得られます: P(x) = 4x³ – x² + 3x。
完全な多項式:すべての可能な指数 (最高次数から独立項まで) を含む単項式を含む多項式を見つけた場合、それは完全な多項式であると言います。たとえば、次の式: P(x) = 3 x² + 2x – 4 は、2 と 0 の間に欠落している指数がないため、このタイプになります。
同次多項式:各単項式の絶対次数が等しい多項式です。変数の指数は異なる値を持つことができますが、すべての単項式における変数の指数の合計は必ず同じでなければなりません。たとえば、P(x) = x²y³z + 3 x ⁴ yz、2 つの合計は 6 2 + 3 + 1 = 4 + 1 + 1 = 6 となります。
同一の多項式:同じ項の係数を共有する 2 つ以上の多項式が見つかった場合、それらは同一の多項式であると言います。以下に 2 つの多項式間の例を示します: P(x) = 2x + 27 と Q(x) = 5 (x + 3) – 3 (x – 4)。これらは各指数の係数を共有するため同一になります。 : 2x = 5x – 3x および 27 = 15 + 12。
ゼロ多項式:この多項式にはゼロ係数 (ゼロに等しい) しかないため、多項式の合計値もゼロになります。多項式 P(x) = 0x³ + 0x² – 0x – 0 は、このタイプの多項式の明確な例ですが、Q(x) = 0 と混同しないでください。この場合、方程式を作成しますが、式は作成されません。 Q(x) のすべての係数が 0 であることを意味するわけではありません。

多項式の数値

多項式の数値は、この式の変数を数値に置き換えることによって得られる結果です。この多項式を結合演算であるかのように解く必要があるだけです。次に、このような式の数値を取得するために使用できる 3 つの方法について説明します。

直接置換:多項式の各変数に対応する値が直接与えられた場合、これらの変数をこれらの数値に置き換えるだけです。このように、多項式 P(x) = 2x² – x + 4 があり、x = 3 であると伝えられた場合、多項式の数値は 2 · 3² – 3 + 4 = 19 に等しくなります。
変数の解決:変数の値が直接与えられないが、等価性が得られる場合にこのケースを適用します。たとえば、P(2) P(x – 1) = x³ – 2x + 1 が true の場合、まず方程式 2 = x – 1 を解き、x = 3 を取得します。最後に、次の式に 3 を代入する必要があります。 x、3³ – 2 · 3 + 1 = 22 となります。
変数の変更:多項式 P(x) = 4x – 2 があり、P(x + 2) のこの値を知りたい場合。次に、式内のすべての x を a(x+2) に変更する必要があります。そうは言っても、この最後に解決された例がどのようになるかを見てみましょう: P (x + 2) = 4 (x + 2) – 2。

多項式を使用した演算

以下では、常に演算の階層に従い、多項式を使用して基本的な四則演算を解く方法を説明します。各セクションには、それぞれのケースでどのように進めるかを知るための小さな理論といくつかの実践的な例が含まれています。

多項式の加算

多項式を追加するには、多項式は類似の項でのみグループ化できるという事実を考慮する必要があります。そのため、多項式 P(x) = 3x³ – x² + 2x – 4 および Q(x) = 2x² + 3x – 2 があるとします。したがって、P(x) + Q(x) を作成するには、同じ指数を伴う 2 つの多項式の係数を加算します。 P(x) + Q(x) = 3x³ + (-x) ² + 2x²) + ( 2x + 3x) + (-4 -2) = 3x³ + x² + 5x – 6. 要約すると、類似した各項の係数をグループ化して加算し、最終的にはすべての項を 1 つの多項式で表現したと言えます。。

多項式の減算

多項式の減算は加算と同じ方法で解決されますが、唯一の違いは明らかに記号です。次に、類似した用語をグループ化し、すべてを減算して 1 つの式に変換します。以下に例を使用して説明します。P(x) = 5x³ – 2x² + x – 3 および Q(x) = 3x² + 5x + 4、その後 P(x) – Q(x ) = 5x³ + (-2x² + 3x²) + (x + 5x) + (-3 + 4) = 5x³ + x² + 6x + 1。

多項式乗算

このタイプの掛け算を解くときは、少し複雑になることがありますが、これから説明するすべての手順に従えば問題ありません。この数学的演算では、すべての単項式が他のすべての単項式と作用します。これは、類似した項を掛け合わせるだけではないことを意味します。さらに、係数が変化するだけでなく、指数も変化します。この例を使用すると、すべてがよりよく理解できるようになります: P(x) = 2x² + 3x – 1 および Q(x) = 2x + 3:

P(x) Q(x) = ( 2x² + 3倍–1 )・( 2倍+ 3 ) = 2x² · 2倍+ 2x² · 3 + 3倍· 2倍+ 3倍· 3 + (-1 ）・ 2倍+ (-1 ）・ 3 = 4×3 + 6×2 + 6×2 + 9x – 2x – 3 = 4×3 + 12x² + 7x – 3

基本的に、多項式の各項の係数を 2 番目の項のすべての係数で乗算し、 a ⁿ · a ^m = a ^n+mのべき乗特性を適用します。

多項式の割り算

最後に、多項式の割り算の解き方を説明するだけで済みます。基本的には、割り算の分配特性を適用する必要があります: (a + b + c) ÷ d = (a ÷ d) + (b ÷ d) + (c ÷ d)。また、次のべき乗のプロパティをⁿ ÷ a ^m = a ^nmに適用します。これを簡単な例で見てみましょう: P(x) = 3x³ – 6x² + 9x および Q(x) = 3x。

P(x) ÷ Q(x) = ( 3×3 – 6x² +9倍) ÷ 3倍= ( 3×3 ÷ 3倍) + ( 6x² ÷ 3倍) + (9倍÷ 3倍) = x² – 2x + 3

多項式を使用してこれらすべての演算を解決する方法を確認し終えたので、それを実際に適用する方法を理解できたと思います。しかし、これは当てはまらず、もう少し練習を続けたいと思われる場合は、このページで解決済みの演習をいくつか参照することをお勧めします。これらは、これらすべての数学的概念の内面化を完了するのに役立ちます。

多項式の因数分解

多項式を因数分解するには、この最後のリンクの記事で説明されているように手動で行うことも、 Ruffini 計算機を使用して行うこともできます。すぐに実行したい場合は、この 2 番目のオプションを使用することをお勧めしますが、因数分解の方法を学習しているだけの場合は、手動で練習することをお勧めします。これを行う方法は、状況に応じて選択する必要があります。

関数電卓で多項式を解く

現在、さまざまな関数電卓が市場に出回っています。ただし、多項式を解くことができる安価な電卓をお探しの場合は、 Casio FX-991SPX IIをお勧めします。使いやすく、非常に強力で高機能なので、中学生および高校生の数学の学生に最適です。以下では、このスタイルの数式が、このモデルまたは同様のカシオモデルを使用してどのように解かれるかを簡単に説明します。

まず変数の数値を入力し、それを書き込んでから、 「STO」+変数の文字 ( x など) を押す必要があります。したがって、すべての変数が定義されたら、すべての変数とすべての数値をそのまま多項式に記述するだけで済みます。最後に、等号キーを押す必要があります。これにより、多項式の数値と同等の結果が得られます。