垂直線（直角度） -

このページでは、垂直線についてのすべてがわかります。垂直線とは何か、2 つの線が垂直である場合、もう一方の線に垂直な線を計算する方法、そのプロパティなどです。さらに、例も表示され、次のことができるようになります。段階的に解決された演習で練習します。

2本の垂直線とは何ですか?

数学では、 2 本の線が 4 つの等しい直角 (90 度) を形成する点で交差するとき、垂直になります。

さらに、2 本の垂直線の方向ベクトルも垂直でなければなりません。

2本の線の直角度は一般的に次の記号で表されます。

$\perp .$

一方、平面では、2 つの線の間の相対位置の概念には 4 つの可能性があることを思い出してください。2 つの線は、割線、垂直、一致、または平行の可能性があります。必要に応じて、Web サイトで各線種の意味を確認できます。

2 本の線が垂直かどうかはどうやってわかりますか?

2 本の線が垂直であるかどうかを判断するには、方向ベクトルから、または傾きによって判断する 2 つの方法があります。以下に両方の方法の説明を示します。目的は同じですが、線の表現方法によってそれぞれ異なるため、両方の手順を理解しておくことをお勧めします。

線の方向ベクトルから

2 本の線が垂直であるかどうかを知る 1 つの方法は、問題の線の方向ベクトルを使用することです。方向ベクトルは線の方向を示すベクトルであることを思い出してください。

2 本の垂線の方向ベクトルも互いに直交します。したがって、 2 つの直線の方向ベクトルの内積が 0 に等しい場合、それは直線が垂直であることを意味します。

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s =0 \quad \longrightarrow \quad r \perp s$

例を使用して、2 つの直線の垂直度がどのように決定されるかを見てみましょう。

$\displaystyle r: \ \begin{cases} x=3-2t \\[2ex] y=6+3t \end{cases}\qquad \qquad s: \ \begin{cases} x=4+3t \\[2ex] y=-2+2t \end{cases}$

両方の線はパラメトリック方程式として表現されるため、各線の方向ベクトルの成分はパラメータの前にある数値になります。

$t:$

$\vv{\text{v}}_r =(-2,3) \qquad \qquad \vv{\text{v}}_s=(3,2)$

各線の方向ベクトルがわかったら、ベクトル間の積を計算してそれらが垂直かどうかを確認します。

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s = (-2,3)\cdot (3,2) = -2\cdot 3 +3\cdot 2= \bm{0}$

2 つのベクトルの内積は 0 であるため、線は垂直になります。

ラインの傾き

2 本の線が垂直かどうかを判断するもう 1 つの方法は、その傾きを使用することです。線の傾きが係数であることを思い出してください。

$m$

陽的な方程式と直線の点と傾きの方程式の関係。

$y=mx+n \qquad \qquad y-y_0=m(x-x_0)$

また、線の傾きも係数から求めることができます。

$A$

そして

$B$

直線の暗黙的な (または一般的な) 方程式の次の式:

$Ax+By+C= 0 \ \longrightarrow \ m = -\cfrac{A}{B}$

したがって、2 つの垂直線の傾きは逆であり、符号が反対です。つまり、次の等式が常に満たされます。

$r \perp s \quad \longrightarrow \quad m_r=-\cfrac{1}{m_s}$

したがって、2 つの異なる直線の傾きの積が -1 に等しい場合、これは直線が垂直であることを意味します。

$m_r\cdot m_s=-1\quad \longrightarrow \quad r \perp s$

たとえば、次の 2 つの線は垂直です。

$r: \ y=2x+4 \qquad \qquad s: \ y=-\cfrac{1}{2} \ x-5$

傾きから、それらが互いに垂直な 2 本の線であることがわかります。各線の傾きは次のとおりです。

$m_r = 2 \quad \quad m_s=-\cfrac{1}{2}$

次に、傾きを乗算します。

$\displaystyle 2 \cdot \left(-\frac{1}{2} \right) = -\cfrac{2}{2} = \bm{-1}$

2 つの傾き間の積は -1 に相当します。これは、実際には互いに垂直な 2 本の線を意味します。

別の線に垂直な線を計算するにはどうすればよいですか?

難しいように思えるかもしれませんが、別の線に垂直な線を見つけるのは非常に簡単です。これに必要なのは、線に垂直な方向ベクトルと、その線に属する点だけです。

唯一の難点は、前と同様に、手順が直線が表現される方程式の種類に依存することです。なぜなら、別の線に垂直な線は、方向ベクトルまたは傾きから計算できるからです。

右の方向ベクトルより

別の指定された線に垂直な線は、その方向ベクトルを使用して見つけることができます。例を使ってこれがどのように行われるかを見てみましょう。

直線に垂直な直線を計算します
$r$

点を通過するもの

$P(5,-1)$

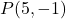
。まっすぐであること

$r:$

$\displaystyle r : \ 3x+2y-1=0$

最初に行う必要があるのは、線の方向ベクトルを特定することです。この場合、直線は一般 (または暗黙的な) 方程式の形式で定義されるため、直線の方向ベクトルのデカルト座標は直線の係数 A と B を使用して取得できます。

$\vv{\text{v}}_r =(-B,A)=(-2,3)$

そして、線の方向ベクトルがわかったら、それに垂直なベクトルを計算する必要があります。これを行うには、ベクトルの座標を挿入し、そのうちの 1 つ (必要なもの) の符号を変更するだけです。

$\vv{\text{v}}_\perp =(3,2)$

これで、線の方向ベクトルがわかりました。したがって、直線の暗黙的な方程式は次のようになります。

$\left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}_\perp= (3,2) \end{array} \right\}\longrightarrow \begin{array}{l}A=2 \\[2ex] B=-3 \end{array}$

$Ax+By+C \ \longrightarrow \ 2x-3y+C=0$

したがって、パラメーター C を決定するだけで十分です。これを行うには、直線に属する点を方程式に代入し、結果として得られる方程式を解きます。

$P(5,-1)$

$2x-3y+C=0 \ \xrightarrow{x=5 \ ; \ y=-1} \ 2\cdot 5-3\cdot (-1)+C=0$

$10+3+C=0$

$13+C=0$

$C=-13$

結論として、垂線の方程式は次のようになります。

$\bm{2x-3y-13=0}$

線路の傾きから

特定の線に垂直な線を見つけるもう 1 つの方法は、その傾きから求めることです。この種の問題がどのように解決されるかを例で見てみましょう。

直線に垂直な直線を計算します
$r$

点を通過するもの

$P(0,1)$

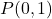
。まっすぐであること

$r:$

$\displaystyle r : \ y=4x-3$

線の傾き

$r$

東：

$m_r = 4$

線の傾きがわかったら、次は垂線の傾きを見つける必要があります。上のセクションで見たように、2 本の垂直線の傾きは逆であり、符号が変わります。したがって、垂線の傾きを決定するには、見つかった傾きを反転し、その符号を変更する必要があります。

$m_\perp =-\cfrac{1}{4}$

したがって、垂線の明示的な方程式は次のようになります。

$y= mx+n$

$y=-\cfrac{1}{4} \ x + n$

最後に、点の座標を直線の方程式に代入して、垂線の原点の縦座標を計算します。

$P(0,1)$

$y=-\cfrac{1}{4} \ x + n \ \xrightarrow{x=0 \ ; \ y=1} \ 1 =-\cfrac{1}{4}\cdot 0 + n$

$1 = n$

つまり、垂線の方程式は次のようになります。

$\bm{y=-}\mathbf{\cfrac{1}{4}} \ \bm{x + 1}$

垂線の性質

すべての垂直線には次の特性があります。

対称関係: ある線が別の線に垂直である場合、その線は最初の線にも垂直です。

$r \bm{\perp} s \ \longrightarrow \ s \bm{\perp} r$

非反射特性: 明らかに、線自体に対して垂直になることはできません。

$r \ \cancel{\bm{\perp}}} \ r$

定理:ユークリッド幾何学 (R2) では、3 番目の線に垂直な線のペアは必ず平行でなければなりません。つまり、ある線が別の線に垂直で、その線が 3 番目の線にも垂直である場合、最初と最後の線は平行になります。

垂直線の問題を解決しました

演習 1

次の線のうち、その線に垂直なのはどれですか

$r: y=3x+4$

$a : \ y=3x-\cfrac{1}{3}$

$b : \ y=-\cfrac{1}{3} \ x+5$

$c : \ y=-4x-3$

$d : \ y=\cfrac{1}{3} \ x-5$

$e : \ y=-\cfrac{1}{3} \ x-2$

解決策を参照

線の傾き

$r$

は 3:

$m_r=3$

そして、2 本の垂直線の傾きは逆で符号が反対であるため、その線に垂直な線の傾きは次のようになります。

$r$

でなければなりません：

$m_\perp=-\cfrac{1}{3}$

したがって、線に垂直な線は

$r$

傾きが次の値に等しいものです

$-\cfrac{1}{3}$

。つまり、ラインは

$\bm{b}$

そして

$\bm{e}.$

演習 2

次の 2 つの線が垂直であるかどうかを確認します。

$\displaystyle r: \ \begin{cases} x=4-t \\[2ex] y=1-3t \end{cases}\qquad \qquad s: \ \cfrac{x-2}{4} = \cfrac{y+3}{6}$

解決策を参照

権利

$r$

はパラメトリック方程式の形式で表され、その線の方向ベクトルの成分はパラメータの前の数字になります。

$t:$

$\vv{\text{v}}_r =(-1,-3)$

一方、直線は、

$s$

は連続方程式の形式で定義されるため、その方向ベクトルの座標は分母の数になります。

$\vv{\text{v}}_s =(4,6)$

各線の方向ベクトルがわかったら、2 つのベクトルの積を計算することで、それらが垂直であるかどうかを確認できます。

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s = (-1,-3)\cdot (4,6) = -1\cdot 4 + (-3)\cdot 6= -22 \bm{\neq 0}$

2 つのベクトルの内積はゼロではないため、線は垂直ではありません。

演習 3

直線に垂直な直線を求めます

$r$

点を通過するもの

$P(-2,1)$

。まっすぐであること

$r:$

$\displaystyle r : \ 4x-y+5=0$

解決策を参照

最初に行う必要があるのは、線の方向ベクトルを特定することです。この場合、直線は一般 (または暗黙的な) 方程式の形式で定義されるため、その方向ベクトルは次のようになります。

$\vv{\text{v}}_r =(-B,A)=(1,4)$

線の方向ベクトルがわかったら、それに垂直なベクトルを計算する必要があります。これを行うには、ベクトルの座標を挿入し、そのうちの 1 つ (必要なもの) の符号を変更するだけです。

$\vv{\text{v}}_\perp =(4,-1)$

したがって、直線の暗黙的な方程式は次のようになります。

$\left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}_\perp= (4,-1) \end{array} \right\}\longrightarrow \begin{array}{l}A=-1 \\[2ex] B=-4 \end{array}$