垂直漸近線 - マソリティ

ここでは、関数の垂直方向の漸近線が何であるかを示します (例とともに)。関数の垂直方向の漸近線を見つける方法も説明しており、さらに、段階的に解かれた演習で練習することができます。

垂直漸近線とは何ですか?

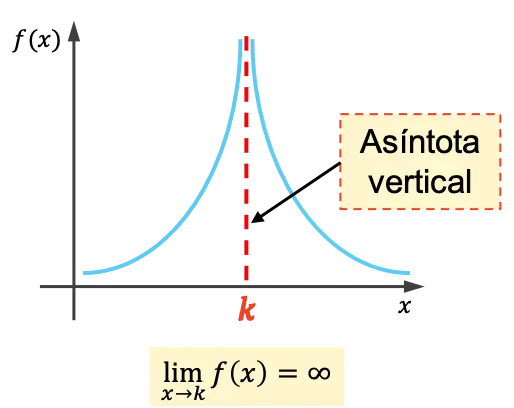
関数の垂直漸近線は、グラフが決して交わることなく無限に近づく垂直線です。したがって、垂直漸近線の方程式はx=kになります。ここで、 kは垂直漸近線の値です。

つまり、 x がkに近づくときの関数の限界が無限大である場合、 kは垂直漸近線になります。

関数の垂直漸近線を計算する方法

関数の垂直漸近線を計算するには、次の手順に従う必要があります。

関数のドメインを見つけます。すべての点がドメイン内にある場合、関数には垂直方向の漸近線がありません。
ドメイン内にない点における関数の極限を計算します。
関数の垂直方向の漸近線は、制限が無限大となるすべての値になります。

関数には複数の垂直漸近線が存在する可能性があることに注意してください。たとえば、正接関数のグラフには、無限に多くの垂直漸近線があります。

➤参照:正接関数の特性

垂直漸近線の例

例として、次の有理関数のすべての漸近線を見つけて、それがどのように行われるかを確認します。

$f(x)=\cfrac{1}{x-2}$

一般に、垂直漸近線がある点は関数の領域に属しません。したがって、最初に関数の定義域を計算します。

これは有理関数であるため、分母がいつ消えるかに注目して、ドメインに属さない点を特定します。

$x-2=0$

$x=2$

したがって、関数の定義域は x=2 を除くすべて実数です。

$\text{Dom } f = \mathbb{R} - \{2\}$

したがって、 x=2 は関数の垂直漸近線になる可能性があります。これを検証するには、この時点での関数の制限を計算する必要があります。

$\displaystyle \lim_{x \to 2} \frac{1}{x-2}=\frac{1}{2-2}=\frac{1}{0}=\infty$

この場合、ゼロ間の数値の不確定性が得られたため、極限を解決するには、横方向の極限を計算して、それがプラス無限大なのかマイナス無限大なのか、それとも極限が存在しないのかを知る必要があります。ただし、垂直方向の漸近線を計算する場合、横方向の極限を行う必要はありませんが、この不確定性が得られれば、それが垂直方向の漸近線であると言えるだけで十分です。

つまり、x が 2 に近づくときの関数の極限は無限大となるため、 x=2 は垂直方向の漸近線になります。

以下は関数をグラフで表したものです。ご覧のとおり、これは (左と右の両方から) x=2 の線に非常に近づいていますが、垂直漸近線であるため、決して交差しません。

さらに、グラフから点 x=2 における関数の横方向の限界を推測できます。

$\displaystyle \lim_{x \to 2^-} \frac{1}{x-2} = -\infty \qquad \lim_{x \to 2^+} \frac{1}{x-2} = +\infty$

垂直漸近線の問題を解決しました

演習 1

次の有理関数の垂直漸近線を計算します。

$\displaystyle f(x)=\frac{3x-1}{2x-1}$

解決策を参照

関数の垂直方向の漸近線を計算する公式はありませんが、関数の定義域を見つけて、関数が定義されていない点で極限が無限大となるかを確認する必要があります。

したがって、ドメインに属さない点を見つけるために、有理関数の分母を 0 に設定します。

$2x -1 =0$

$2x= 1$

$x = \cfrac{1}{2}$

したがって、関数の定義域は x=1/2 を除くすべて実数です。

$\text{Dom } f = \mathbb{R} - \left\{ \cfrac{1}{2} \right\}$

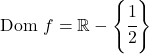
したがって、x=1/2 は垂直方向の漸近線になる可能性があります。これを確認するために、この時点での関数の制限を計算します。

$\displaystyle \lim_{x \to \frac{1}{2} } \cfrac{3x-1}{2x-1} = \cfrac{3\cdot\cfrac{1}{2}-1}{2\cdot\cfrac{1}{2}-1} = \cfrac{ \cfrac{3}{2} -1 }{\cfrac{2}{2} -1 } = \cfrac{ \cfrac{1}{2} }{1-1}=\cfrac{\cfrac{1}{2}}{0} =\infty$

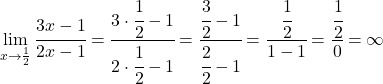
したがって、この点での関数の極限は無限大を与えるため、 x=1/2 は垂直漸近線になります。

演習 2

次の分数関数のすべての垂直漸近線を求めます。

$\displaystyle f(x)=\frac{2x+1}{x^2-9}$

解決策を参照

まず、分数の分母をゼロに設定して、どの値が関数の領域に含まれないかを確認します。

$x^2-9=0$

不完全な二次方程式を解きます。

$x^2=9$

$x=\pm 3$

したがって、有理関数の定義域は次のようになります。

$\text{Dom } f = \mathbb{R} - \left\{3, -3\right\}$

したがって、これら 2 つの値のどちらが垂直方向の漸近線であるかを判断するには、各点での関数の極限を解きます。

$\displaystyle\lim_{x \to 3}\frac{2x+1}{x^2-9}=\frac{2\cdot3+1}{3^2-9}=\frac{7}{9-9}=\frac{7}{0}=\infty$

$\displaystyle\lim_{x \to -3}\frac{2x+1}{x^2-9}=\frac{2\cdot(-3)+1}{(-3)^2-9}=\frac{-5}{9-9}=\frac{-5}{0}=\infty$

2 つの極限は無限大を与えるため、 x=3 と x=-3 は問題の関数の 2 つの垂直漸近線になります。

演習 3

次の有理関数の垂直方向の漸近線をすべて見つけます (ある場合)。

$\displaystyle f(x)=\frac{x+3}{x^2+2x-3}$

➤参照: ゼロ間のゼロ不確定性

解決策を参照

まず、二次分母の方程式を解いて、分数の分母を打ち消す値を見つけます。

$x^2+2x-3=0$

$\begin{aligned}\displaystyle x&=\cfrac{-b\pm\sqrt{b^2-4ac}}{2a}=\cfrac{-2\pm\sqrt{2^2-4\cdot1\cdot(-3)}}{2\cdot1}=\\[3ex]\displaystyle &=\cfrac{-2\pm\sqrt{16}}{2}=\cfrac{-2\pm 4}{2}=\begin{cases}\cfrac{-2+4}{2}=1\\[3ex]\cfrac{-2-4}{2}=-3\end{cases}\end{aligned}$

したがって、関数のドメインは次のようになります。

$\text{Dom } f = \mathbb{R} - \left\{1, -3\right\}$

したがって、最初に x=1 における関数の極限を計算します。

$\displaystyle\lim_{x \to 1}\frac{x+3}{x^2+2x-3}=\frac{1+3}{1^2+2\cdot 1-3}=\frac{4}{0}=\infty$

一方、x が -3 に向かう傾向がある場合の関数の極限を解きます。

$\begin{array}{l}\displaystyle\lim_{x \to -3}\frac{x+3}{x^2+2x-3}=\frac{-3+3}{(-3)^2+2\cdot(-3)-3}=\frac{0}{0}=\\[3ex]\displaystyle =\lim_{x \to -3}\frac{\cancel{x+3}}{(x-1)\cancel{(x+3)}}=\lim_{x \to -3}\frac{1}{x-1}=\frac{1}{-3-1}=-\frac{1}{4}\end{array}$

前の制限では、ゼロ間の不定形式ゼロが得られるため、これを解決するには、多項式を因数分解する必要があります。制限をどのように解決したかについて疑問がある場合は、演習ステートメントへのリンクで、この種の不確定性を解決する方法の完全な説明を参照してください。

この場合、点 x=1 における関数の極限のみが無限大を与えるため、 x=1 は関数の唯一の垂直方向の漸近線になります。

垂直漸近線とは何ですか?

関数の垂直漸近線を計算する方法

垂直漸近線の例

垂直漸近線の問題を解決しました

演習 1

演習 2

演習 3

コメントする 返信をキャンセル

コメントする返信をキャンセル