同一平面上にある (または同一平面上にある) 点

このページでは、共面 (または共面) 点とは何か、および特定の点が共面であるかどうかを確認する方法を説明します。さらに、例を見て、解決された同一平面上の問題を練習することができます。

同一平面上点とは何ですか?

解析幾何学では、同一平面上(または同一平面上)の点の意味は次のとおりです。

同一平面上にある点は、同じ平面に属する点です。

したがって、最低 3 つの点で平面を形成できるため、2 つまたは 3 つの点は常に同一平面上にあります。一方、点が 4 つ、5 つ以上ある場合は、いくつかの点が同じ平面に含まれておらず、したがってそれらが同一平面上にない可能性があります。

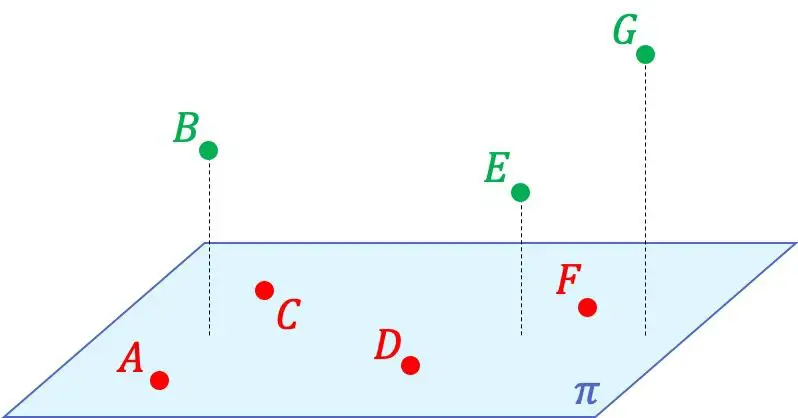
たとえば、上のグラフ表示では、点 A、C、D、および F が同じ平面内に含まれているため、これらの点が互いに同一平面上にあることがわかります。一方、これら 4 つの点は、すべての点を含む空間内に平面を形成できないため、点 B、E、および G と同一平面上にありません。

この特性から、同一平面上の点によって定義されるベクトルも同一平面上のベクトルである、つまり、それらは同じ平面内に含まれると推測できます。

点が同一平面上にあるのはいつですか?

同一平面上にある点の定義で見たように、2 つまたは 3 つの点は常に同一平面上にありますが、3 つ以上の点は同一平面関係を尊重する必要はありません。

したがって、4 つ以上の点が同一平面上にあるかどうかを判断するには、主に 2 つの方法があります。

点が同一平面上にあるかどうかを知る 1 つの方法は、点によって決定されるベクトルによって決まります。これらのベクトルが同一平面上にある場合、点も同一平面上にあります。

明らかに、この方法を適用するには、ベクトルがいつ同一平面上にあるのかを知る必要があります。ただし、ベクトルのセットが同一平面上にあるかどうかを判断する方法もいくつかあるため、ベクトルが同一平面内にあるかどうかを確認する方法を確認することをお勧めします。ここでは、2 つ、3 つ、4 つ以上のベクトルが同一平面上にある場合を見つけるために存在するすべての手順と、例と解決された演習が見つかります。

点のセットが同一平面上にあるかどうかを知るもう 1 つの方法は、そのセット内の 3 つの点によって形成される平面の方程式を見つけることです。他の点がこの方程式を満たす場合、セット内のすべての点が同一平面上にあることを意味します。

問題によって異なりますが、平面の方程式を計算するよりもベクトルが同一平面上にあるかどうかを確認する方がはるかに簡単で高速であるため、2 つの方法のうち最初の方法を使用することをお勧めします。ただし、当然のことながら、お好みの方を使用してください。

同一平面上の点の問題を解決

演習 1

次の 3 つの点が同一平面上にあるかどうかを判断します。

$A(3,5,1)$

$B(0,-2,3)$

$C(4,-1,2)$

解決策を参照

この場合、3 つの点がどのようなものであっても常に同一平面上にあるため、計算を行う必要はありません。

演習 2

次の 4 つの点が同一平面上にあるかどうかを判断します。

$A(1,2,0)$

$B(-1,3,4)$

$C(1,0,-1)$

$D(2,5,-3)$

解決策を参照

4 つの点が同一平面上にあるためには、それらの点によって決定されるベクトルが同一平面上にある必要があります。したがって、これらのベクトルを計算します。

$\vv{AB} = B- A = (-1,3,4)-(1,2,0) = (-2,1,4)$

$\vv{AC} = C- A = (1,0,-1)-(1,2,0) = (0,-2,-1)$

$\vv{AD} = D- A = (2,5,-3)-(1,2,0) = (1,3,-3)$

次に、ベクトルによって形成される行列を構築しましょう。

$\displaystyle A= \begin{pmatrix} -2&1&4 \\[1.1ex]0&-2&-1 \\[1.1ex] 1&3&-3\end{pmatrix}$

結果として得られるベクトルが同一平面上にあるためには、前の行列のランクが 2 に等しくなければなりません。また、このためには、3×3 行列全体の行列式が 0 に等しくなければなりません。

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix} -2&1&4 \\[1.1ex]0&-2&-1 \\[1.1ex] 1&3&-3\end{vmatrix} =-11\neq 0$

$rg(A)=3$

ただし、行列全体の行列式は非ゼロであるため、行列のランクは 3 となり、したがって4 つの点は同一平面上にありません。

演習 3

次の 5 つの点が同一平面上にあるかどうかを確認します。

$A(3,1,1)$

$B(0,0,2)$

$C(4,-2,-1)$

$D(-1,1,3)$

$E(2,4,3)$

解決策を参照

5 つの点すべてが同一平面上にあるためには、それらの点によって定義されるベクトルが同一平面上にある必要があります。したがって、これらのベクトルを計算します。

$\vv{AB} = B- A = (0,0,2)-(3,1,1) = (-3,-1,1)$

$\vv{AC} = C- A = (4,-2,-1)-(3,1,1) = (1,-3,-2)$

$\vv{AD} = D- A = (-1,1,3)-(3,1,1) = (-4,0,2)$

$\vv{AE} = E- A = (2,4,3)-(3,1,1) = (-1,3,2)$

次に、ベクトルで構成される行列を構築しましょう。

$\displaystyle A= \begin{pmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{pmatrix}$

結果として得られるベクトルが同一平面上にあるためには、前の行列のランクが 2 に等しくなければなりません。したがって、行列式によってベクトルの行列のランクを計算し、それらが同一平面上にあるかどうかを確認します。

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -4&0&2\end{vmatrix} = 0 \qquad \begin{vmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -1&3&2\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} -3&-1&1 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{vmatrix} = 0 \qquad \begin{vmatrix} 1&-3&-2 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{vmatrix} = 0$