この記事では、関数の双曲線逆余接を導出する方法を説明します。さらに、双曲線逆余接の導関数の解決例も表示されます。
双曲線逆余接の導関数の公式
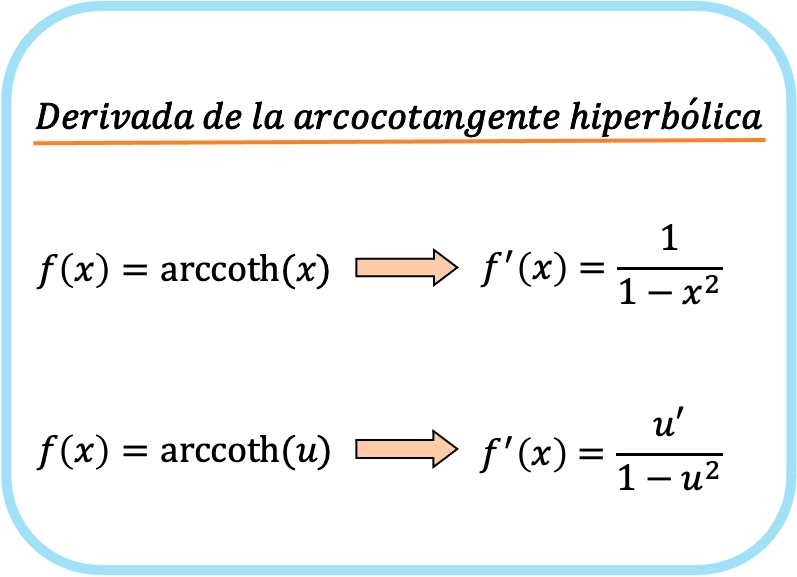
x の双曲線逆余接の導関数は、1 の 1 から x の 2 乗を引いたものです。
![]()
したがって、関数の双曲線逆余接の微分値は、その関数の微分値を 1 で割った商からその関数の 2 乗を引いたものに等しくなります。
![]()
2 番目の式は最初の式と似ていますが、連鎖規則が適用されるため、実際には同じ式とみなされる可能性があることに注意してください。
一部の数学の本では、このタイプの逆三角関数の微分が次のようになっているのを目にすることがあります。
![]()
しかし、よく見るとこれらは同じ式であり、分数の分子と分母に -1 が掛けられているだけの違いがあります。
双曲線逆余接の導関数の例
例1
![]()
双曲線逆余接引数には x とは異なる関数があるため、それを導出するには連鎖規則式を使用する必要があります。
![]()
5x の導関数は 5 なので、分数の分子に 5 を入れ、分母にマイナス 5x の 2 乗を入れます。
![]()
例 2
![]()
この関数の導関数を解くには、次のような双曲線逆余接の導関数の公式を適用する必要があります。
![]()
この場合、三角関数の引数に指数関数があるため、複合関数が得られます。したがって、連鎖規則を使用して関数全体の導関数を見つける必要があります。
![]()
類似商品
- 双曲線逆正接の導関数
- 双曲線正接の導関数
- 双曲線余接の導関数
- 逆余接の導関数
- 逆正接の導関数
- コタンジェントから導出
- タンジェントの導関数