双曲線アークコサインの導関数

このページでは、双曲線逆余弦の導関数 (公式) が何かを説明します。また、関数の双曲線逆余弦の導関数について段階的に解決される演習もあります。そして最後に、このタイプの三角関数の導関数の公式のデモンストレーションを示します。

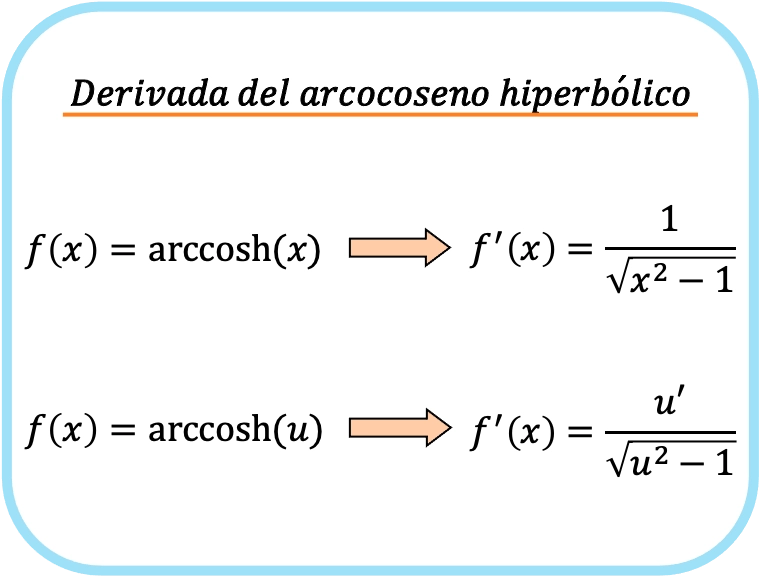
双曲線アークコサインの導関数の公式

x の双曲線逆余弦の導関数は、x の平方根から 1 を引いた値です。

f(x)=\text{arccosh}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{\sqrt{x^2-1}}

したがって、関数の双曲線アークコサインの微分値は、その関数の微分値をその関数の平方根で割った商から 1 を引いた値に等しくなります。

f(x)=\text{arccosh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2-1}}

2 番目の式には連鎖律が含まれているため、任意の双曲線逆余弦を導出するために使用できます。実際、x を u に置き換えると、最初の式が得られます。代わりに、最初の式は x の双曲線逆余弦導関数に対してのみ機能します。

双曲線アークコサインの導関数

双曲線アークコサインは双曲線余弦の逆関数であるため、2 つの関数は関連しています。ここをクリックすると、この三角関数の導関数の公式を確認できます。

➤参照: 双曲線余弦の導関数の公式

双曲線逆正弦導関数の例

例1

f(x)=\text{arccosh}(5x)

双曲線逆余弦の導関数を求めるには、対応する次の式を使用する必要があります。

f(x)=\text{arccosh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2-1}}

したがって、分数の分子には 5x の導関数、つまり 5 を入力する必要があります。また、分母には、引数関数の 2 乗から 1 を引いた平方根を入力するだけで済みます。

f(x)=\text{arccosh}(5x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{5}{\sqrt{(5x)^2-1}}=\cfrac{5}{\sqrt{25x^2-1}}

例 2

f(x)=\text{arccosh}(x^4-5x^2)

この演習で導出される関数は双曲線逆余弦であるため、次の式を使用して導出します。

f(x)=\text{arccosh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2-1}}

したがって、分子には関数の引数の導関数を、分母には 2 から 1 を引いた引数の関数の平方根を書きます。

f(x)=\text{arccosh}(x^4-5x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{4x^3-10x}{\sqrt{\left(x^4-5x^2\right)^2-1}}

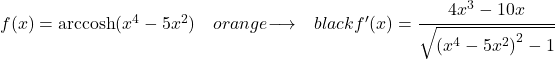
双曲線アークコサインの導関数の証明

最後に、双曲線アークコサインの導関数の公式を示します。

y=\text{arccosh}(x)

まず、双曲線アークコサインを双曲線コサインに変換します。

x=\text{cosh}(y)

等式の両側から次のように推定します。

1=\text{senh}(y)\cdot y'

私たちはあなたをクリアします:

y'=\cfrac{1}{\text{senh}(y)}

ここで、双曲線サインと双曲線余弦を関連付ける三角関数恒等式を使用して、分母を変更します。

\text{cosh}^2(y)-\text{senh}^2(y)=1 \ \longrightarrow \ \text{senh}(y)=\sqrt{\text{cosh}^2(y)-1}

y'=\cfrac{1}{\sqrt{\text{cosh}^2(y)-1}}

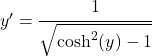
ただし、最初に、x は y の双曲線余弦と同等であると推定したため、方程式は残ります。

y'=\cfrac{1}{\sqrt{x^2-1}}

類似商品

コメントする

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です

上部へスクロール