この記事の下には、すべての難易度をカバーするいくつかの解決済みパーセンテージの問題があります。さらに、通常はパーセンテージを使用して研究されるさまざまなトピックもカバーしています。そうは言っても、問題を自分で解決してみて、完了したら、その結果を同じ演習で提供される結果と比較することをお勧めします。ただし、アクティビティを開始する前に、パーセンテージを使用して問題を解決するための最良の方法について少し説明します。
パーセンテージの問題を解決するにはどうすればよいですか?
パーセントの問題を解決するには、「数学の問題の基本的な解決手順」に従うことをお勧めします。この最後のリンクでは、従うべき手順について詳しく説明しますが、以下ではパーセンテージを解決することを目的とした概要を説明します。
- 問題を理解する:解決策のこの初期段階では、計算するパーセンテージの種類に従って問題を分類する必要があります。一般に、主なタイプは、VAT、増加率、削減率、等価率などです。
- 図を作成する:直面している問題の種類が明確になったら、演習の目的とデータをグラフ化する必要があります。ただし、描画したくない場合は、計算に含まれるデータを含む図をいつでも作成し、それらを相互に関連付けることができます。
- 計算から始めます。後で演習を数学的に解き始めることができます。前のセクションで演習を正しく行っていれば、この部分は簡単です。それ以来、結果を達成するためにいつでも何をすべきかが明確にわかるようになります。
- 結論:最後に結果を表現する必要があります。これは文でも、単に要求された数値でも構いません。そして、問題が終わったら、最初から最後まで分析して結論を出すことを強くお勧めします。
すべてのレベルの割合の問題
パーセンテージを使用した練習問題の解き方を説明したので、いくつかの練習問題で練習を始めてください。次のリストには、パーセントを扱い始めた人向けの練習問題から、非常に複雑なものまで、すべての学年向けの問題が含まれています。自分のレベルがある場合でも、最も簡単なレベル (最初のレベル) から始めて、可能な限りレベルを上げることをお勧めします。
最初の問題
ある学校には生徒が 240 人いて、そのうち 160 人が全科目合格しました。すべての科目に合格した生徒の割合は何ですか?
240 人中 160 人の学生がすべての科目に合格したため、240 人は 100% に相当し、160 人は x% に相当します。 x の価値を調べるために、次の 3 つの簡単なルールを実行します。
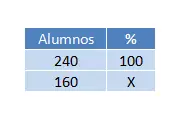
したがって、演算結果は (160 x 100) ÷ 240 = 66.67%、つまり全体の 3 分の 2 となります。したがって、解決策を文で表現したい場合は、パーセンテージで示すこともできます (それがステートメントで尋ねられることです)、または割合で示すこともできます。
2番目の問題
駐車場には 150 台の車があり、そのうち 50% が白、30% が赤、残りが青です。各色の車は何台ありますか?
合計 150 台の車があり、塗装の色に基づいて 3 つの異なるグループに分類する必要があります。したがって、以前と同様に 3 つの計算を行う必要があります。
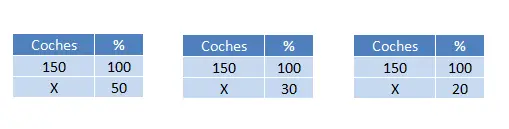
したがって、(50 x 150) ÷ 100 = 75 台、(30 x 150) ÷ 100 = 45 台、および (20 x 150) ÷ 100 = 30 台の 3 つの値が得られます。最後に、これらの結果が正しいかどうかを確認するために、すべてを合計すると、合計が 150 になるはずです。この計算は演習の一部ではなくなりましたが、75 + 45 + 30 = 150 台というチェックとして機能します。
3番目の問題
800 ユーロのテレビを購入したいときに、15% 割引を提供された場合、最終的にテレビにいくら支払うことになりますか?
合計価格は 15% 割引の 800 ユーロです (これは割引率です)。したがって、次の 3 つのルールのうち 1 つだけを解決する必要があります。
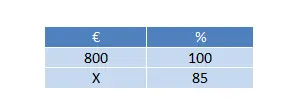
この場合、割引率 (100% – 15%) = 85% に相当する値を計算する必要があります。したがって、最終的な計算は次のようになります: (85 x 800) ÷ 100 = 680 ユーロ。
4番目の問題
給水タンクには 250 リットルの水を貯めていましたが、初日にはこの水の量が総容量の 75% に減りました。そして翌日には残容量が15%減っていました。 2日目が終わった時点でタンクには何立方メートル残っていますか?
この問題を解決するには、ステートメントで確立された順序に従って 2 つの量を計算する必要があります。まず 250 の 75% を計算し、次に残りの金額の 85% (100% – 15%) を計算します。
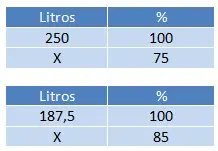
1 日目の残りの量を取得するには、(75 x 250) ÷ 100 = 187.5 リットルの水、(85 x 187.5) ÷ 100 = 159.375 リットルの水の計算を行います。
5番目の問題
2 つの商品 (1 つは 135 ユーロ、もう 1 つは 56 ユーロ) に 21% の VAT が請求された場合、2 つ目の商品には 12% の割引が適用されます。両方の商品を購入すると、最終的にいくらかかりますか?
この問題にはいくつかの計算が含まれます。最初に 2 番目の製品の最終価格 (割引後) を計算し、次に VAT を含む 2 つの製品の価格を計算し、最後に 2 つの価格を加算します。
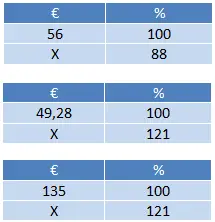
割引を適用した場合の 2 番目の商品の価格は、(88 x 56) ÷ 100 = €49.28 となり、両方の商品に VAT が適用されます: (121 x 49.28) ÷ 100 = €59.63 および (121 x 135) ÷ 100 = € 163.35。最後に、59.63 + 163.35 = €222.98 を合計するだけです。
最後の練習
次のパーセンテージを計算します。
- 540 の 25% = 135
- 160 の 32% = 51.2
- 625 の 46% = 287.5
- 873 の 73% = 637.29
これらの演習を完了し、パーセンテージに関連する問題をさらに知りたい場合は、 このリンクにアクセスすることをお勧めします。そこでは、PDF でパーセンテージの問題が見つかります。これらは、この記事で取り上げたものとあまり違いはなく、パーセンテージの概念を理解することができます。