分数または帯分数は、微積分の分野において非常に重要な数学的概念です。したがって、分数の仕組みと分数の練習問題の解き方を知ることが重要です。分数を使った演算の解き方や、このスタイルの数値を含む他の種類の演習や問題を学ぶかどうかに関わらず、これがこの記事の目的です。それでは、最初の演習から始めましょう。
分数を使った演算の練習
開始するには、分数を含む基本的な演算がいくつか用意されています。必要なのは、それらを解いて簡略化された結果を表現することだけです。したがって、計算を解き終えたら、結果を比較し、提供される修正を確認することをお勧めします。ただし、オンライン分数計算機を使用して結果を確認することもできます。
共通の分母を持つ分数の足し算と引き算
以下に分数の足し算と引き算が 2 つずつ解かれています。自分で解いて結果を比較してみてください。このようにして、このタイプの操作の解決メカニズムを確認します。
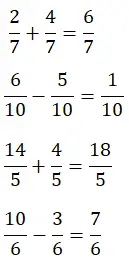
分母の異なる分数の足し算と引き算
ここでレベルを少し上げます。異なる分母を持つ分数の加算と減算を解決するには、まず分母の lcm を見つける必要があるからです。したがって、計算は少し複雑になります。
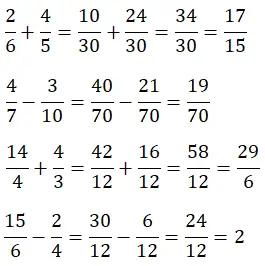
分数の掛け算と割り算
このセクションでは、分数の乗算と除算を解く必要があります。これらの演算は非常に簡単に実行できますが、それでも練習する必要があります。前の 2 つのセクションと同様に、各タイプが 2 つあります。
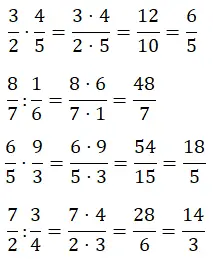
結合分数
最後に、分数を組み合わせた演算である結合分数を解く必要があります。このうち最も複雑な要素は計算です。このタイプの計算を正しく解くには、帯分数の演算に関するすべての知識を集める必要があります。

小数と分数の間の変換の練習
ここで、次の 10 進数を生成分数に、またはその逆に変換してみます。ただし、変換方法が異なるため、正しく行うには、小数のタイプ (正確、純粋周期、または混合周期) を考慮する必要があります。これらの方法を覚えていない場合は、分数に関する記事を読むことをお勧めします。そこでは、小数と分数の間、またはその逆の変換手順がすべて説明されています。以下に解決済みの変換をいくつか示します。自分で実行してみることをお勧めします。

相当する分数の練習
基本的な算術と変換を練習した後、等価な分数から始めます。このセクションでは、いくつかの分数を示し、同等の分数のペアを見つける必要があります。このようにして、等価性の概念を練習し、 分数の簡略化も復習します。

分数の比較の練習
次に、いくつかの分数を示し、記号「<」、「=」、「>」と比較する必要があります。この演習を解くには、共通の分母を見つけて、両方の分数をその分母に変換する必要があります。こうすることで、2 つの分子のどちらが大きいかがわかり、それに応じて行動する必要があります。

数直線上の分数の練習
この演習では、 数直線上に示されるさまざまな分数を順序付ける必要があるため、解決手順は非常に多様になる可能性があります。たとえば、2 つの整数間の距離を分母の値で示される部分で割り、その分数を分子で示されるセグメントに配置できます。
さらに、分子を分母で割って 10 進数を取得し、後で行に入力することもできます。この 2 番目の手順はより基本的なものですが、これが、説明した最初の方法を選択する理由です。そうは言っても、右側に置く必要がある分数は次のとおりです。
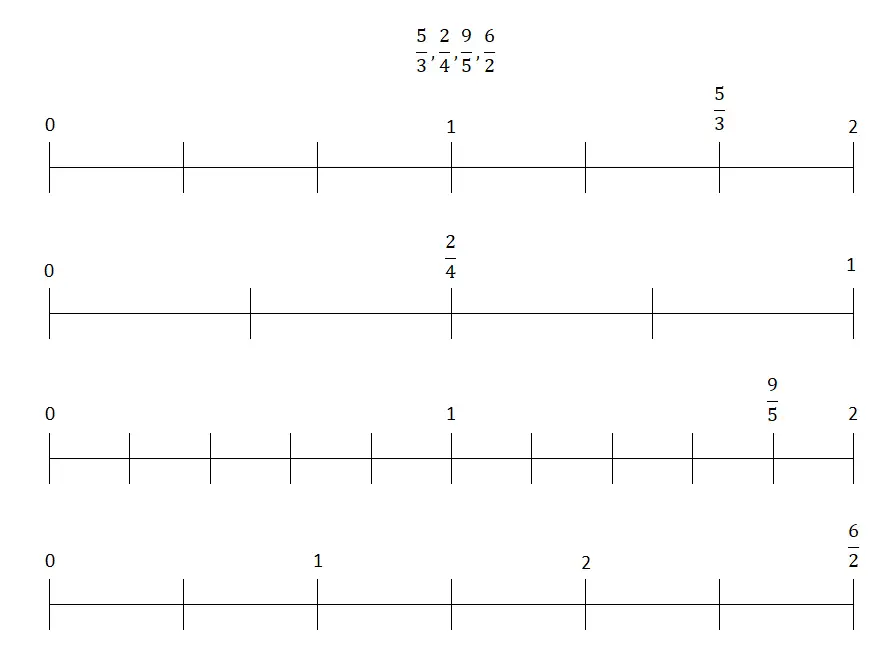
分数の問題
最後に、この記事の最後の部分で、いくつかの分数の問題を扱います。まず最初に、数学の問題を解決するときに使用すべき正しい手順を説明したいと思います。
- 問題を理解する:最初のステップは、よく読んで問題全体を理解することです。こうすることで、宣言で説明されているすべての情報を理解することができます。この部分を正しく実行できれば、解の導き方とすべての計算がわかるので、多くのことを達成したことになります。
- 問題の説明:問題が何であるかを理解したら、それを提示する必要があります。これは、グラフ、図面、またはデータの小さなグラフィック表現を使用して行うことができます。このステップでは、データを接続して問題を解決する方法を考え始めます。
- 問題自体を解決する:その後、問題を数値的に解決し続けることができます。この段階では、前のセクションで提起した理論をテストする必要があります。ここでは実際に行動計画を実行して結果を得る場所なので、非常に集中する必要があります。
- 解決策を解釈する:最後に、すでに解決策が得られたら、これらの結果を解釈し、問題の文脈で理解する必要があります。この最後のステップは非常に重要ですが、多くの人は数値的な結果で十分だと考えているため無視しますが、実際には解決策を 1 つの文に要約する必要があります。
問題1
1 つのタップでプールを満たす場合は 6 時間かかりますが、別のタップで満たす場合は 8 時間かかります。両方の蛇口を同時に使用すると、2 時間でプールのどれくらいが満たされますか?結果を分数で表します。
この問題を解決するには、分数を使用する必要があります。基本的に、私たちがやろうとしていることは、その 2 時間の間に各蛇口がどれだけ満たされるかを個別に計算することです。つまり、最初のタップは 1 時間でタンクの 1/6 を満たし、2 時間を掛けると 2/6 が満たされます。 2 回目のタップでは 1 時間で 1/8 が満たされますが、それに 2 を掛ける必要があり、2/8 になります。
最後に、2 つの部分を加算して、満たされるプールの合計量を取得します。したがって、プールの 2/6 + 2/8 = 7/12 が残ります。
問題2
キャンディーは64個ありますが、そのうちの1/4を友人のマルコスにあげます。次に、キャンディーを 3 個食べ、残りの 2/5 を友人のマリアに渡します。キャンディーはどれくらい残っていますか?整数で表現します。
まず、合計量 64 から 4 分の 1 を減算し、次に得られた結果から 3 を減算し、最後にこのキャンディーの量の 5 分の 2 を減算します。これにより、分数を組み合わせてこれを計算できます。
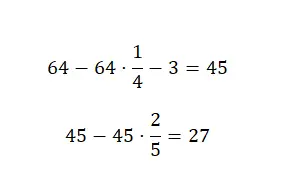
したがって、最終的には 27 個のキャンディーが残ります。
問題3
私たちは 10,000 平方メートルの土地を 3 つの不均等な部分に分割しています。最初のセクションは総面積の 3/6 を表し、2 番目のセクションは前のセクションの半分に相当します。 3 番目のセクションの面積を表すのはどの分数ですか?各セクターの面積は何平方メートルですか?
最初に行うことは、3 番目のプロットの分数を計算することです。これは、分数の非常に単純な減算によって実行されます。次に、数値の小数部を計算して各セクションの面積を計算します。この場合、この数値は 10,000 になります。以下に手順全体を示します。