このページでは、冪等行列とは何かについて説明します。また、完全に理解できるように、このタイプの行列の例をいくつか示します。また、冪等行列を求める公式と、最後に冪等行列のすべてのプロパティも見つかります。
冪等行列とは何ですか?
冪等行列の定義は次のとおりです。
冪等行列とは、それ自体を乗算すると結果として同じ行列が得られる行列です。
![]()
したがって、べき等行列のべき乗は、指数に関係なく、行列自体と等しくなります。
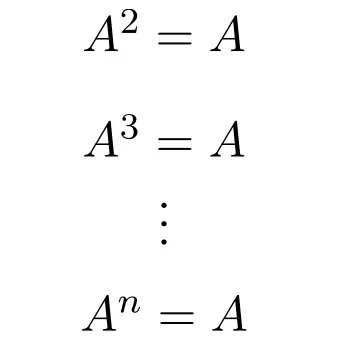
実際、これがこのタイプのボードの名前の由来です。数学における冪等性は、実行回数に関係なく常に同じ結果が得られることを意味する演算であるためです。
冪等行列の例
冪等行列の概念を理解したら、さまざまな次元の例をいくつか見て理解を完了します。
2×2の冪等行列の例
次の次元 2×2 の正方行列は冪等です。
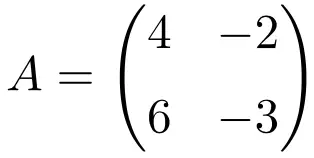
冪等行列であることを確認するために、その二乗を計算します。
![Rendered by QuickLaTeX.com \displaystyle A^2=\begin{pmatrix} 4 &-2 \\[1.1ex] 6 & -3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d83fda6875c8447818921c12f3196a7b_l3.png)
結果は同一なので、冪等行列であることがわかります。
3×3の冪等行列の例
次のサイズ 3×3 の正方行列は冪等です。
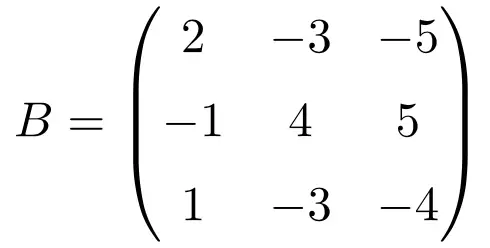
冪等行列が対応していることを確認するには、行列を 2 に引き上げます。
![Rendered by QuickLaTeX.com \displaystyle B^2=\begin{pmatrix} 2 &-3 & -5 \\[1.1ex] -1 & 4 & 5 \\[1.1ex] 1 & -3 & -4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-49a3f48608f3126039c949cde6346acf_l3.png)
結果は元の行列と同じなので、行列の冪等性が証明されます。
2×2の冪等行列の構造
ここではべき等行列を求める公式を示します。さらに興味がある場合は、コメントで以下の式のデモを見ることができますが、少し面倒なので、ここでは冪等行列の式をそのまま残しておきます。

条件が満たされる限り、冪等行列の二次対角要素を任意にできるようにする
![]()
主対角線上の数字は次のようにする必要があります。
![]()
そして
![]()
この式で記述されるすべての行列に加えて、恒等行列を追加する必要があります。これも式を尊重しませんが、冪等行列です。配列が何であるかわからない場合は、 Identity 配列が何であるかを尋ねることができます。
冪等行列のプロパティ
冪等行列には次の特徴があります。
- 冪等行列の行列式は常に 0 または 1 です。
- 単位行列を除いて、他のすべての冪等行列は両方とも特異行列または縮退行列です。つまり、可逆行列ではありません。
- 冪等行列は対角化可能であり、その固有値 (または固有値) は常に 0 または 1 です。
- 冪等行列のトレースは行列のランクに等しい。
- 最後に、冪等行列と累積行列の間には関係があります。

行列が次の場合に限り冪等です。
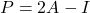
それは回帰的です。