このページでは、円錐曲線の定義、円錐曲線がそれほど重要である理由、存在するさまざまな種類の円錐曲線 (円、楕円、双曲線、放物線) について説明します。さらに、方程式間の違いも確認できます。
円錐曲線とは何ですか?
解析幾何学では、円錐断面 (または単に円錐) は、円錐と平面が円錐の頂点を通過しない場合に、円錐と平面の間のさまざまな交差から生じるすべての曲線です。円錐曲線には、円、楕円、放物線、双曲線の 4 種類があります。
以下は、任意のコーンから取得できる 4 つのセクションです。
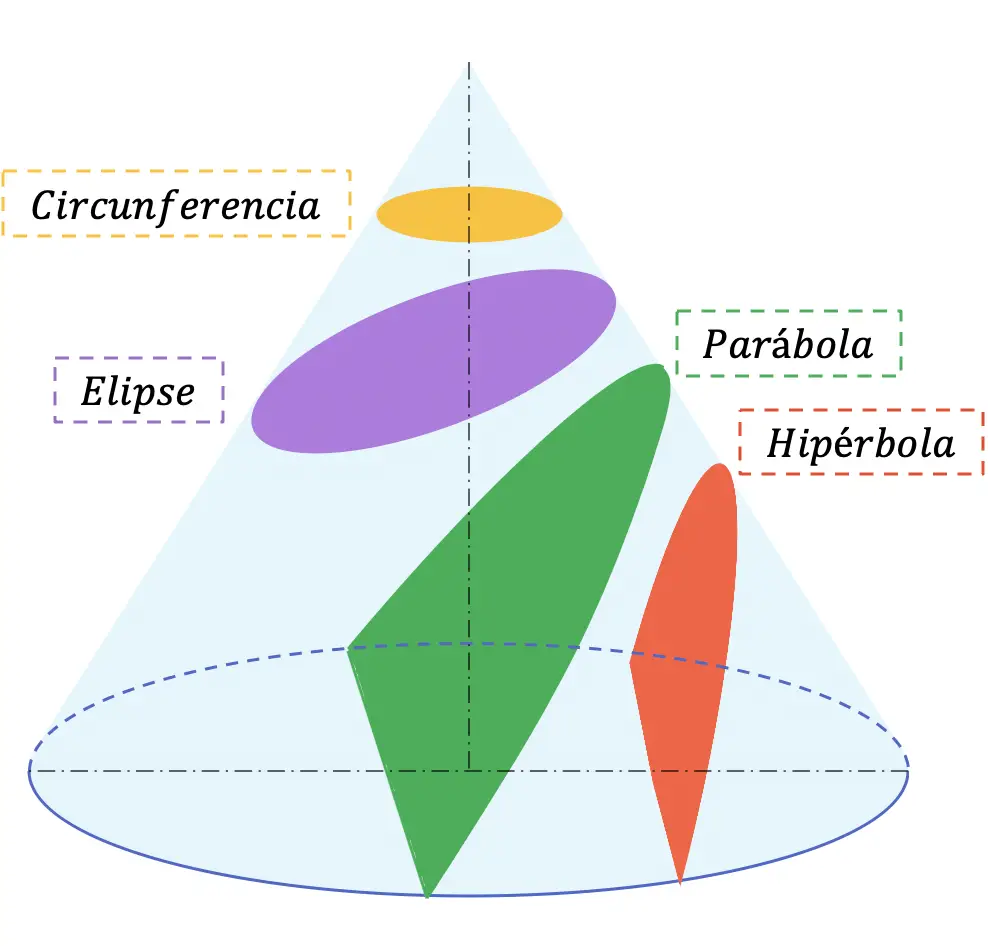
円錐曲線は通常、中等学校 (Bachillerato) の数学と製図の科目で学習されます。
円錐曲線の種類
円錐曲線の概念を理解したら、円、楕円、放物線、双曲線という 4 種類の円錐曲線が存在することを見てみましょう。
周
円周とは、円錐を回転軸に垂直な（底面に平行な）平面で切断したときの円錐の断面のことです。
また、円周とは、中心という定点から等距離にある平面上の点の軌跡のことです。
楕円
楕円は円周に非常によく似た平らで閉じた曲線ですが、その形状はより楕円形です。特に、回転軸に対する角度が発電機の角度よりも大きい斜平面で円錐の表面を切断することによって生じる。
さらに、楕円のすべての点は条件を満たします。楕円は、他の 2 つの固定点 (焦点 F および F’ と呼ばれる) までの距離の合計が一定である平面のすべての点の軌跡です。
たとえ話
数学では、放物線は、固定点 (焦点と呼ばれる) と固定線 (準線と呼ばれる) から等距離にある平面上の点の軌跡です。
幾何学的には、放物線は、円錐の母線の角度に等しい回転軸に対する傾斜角を持つ平面で円錐を切断した結果です。したがって、放物線を含む平面は円錐の母線と平行になります。
この円錐曲線の非常に重要な特性は放物線の方程式です。その状態に応じて放物線の種類を識別できるからです。このリンクでは、放物線のすべての方程式、放物線の要素、その特性、例、演習問題などを見つけることができます。
双曲線
円錐断面としての双曲線は、回転軸に対して円錐の母線が形成する角度より小さい角度で円錐を切断したときに得られます。
数学的には、双曲線は次の特性を満たす平面上の点の軌跡として定義できます。双曲線上の任意の点と 2 つの固定点 (焦点と呼ばれる) の間の距離の差の絶対値は一定でなければなりません。
さらに、これら 2 つの距離を減算した値は、常に双曲線の 2 つの頂点間の距離に等しくなります。
すでに推測していると思いますが、パラメータ値は
双曲線の計算は双曲線の基本です。次のリンクでは、双曲線の説明を参照できます。双曲線がそれほど重要な係数である理由と、双曲線を特徴付けるすべての要素が何であるかがわかります。さらに、 双曲線の方程式がどのようなものであるか、存在するさまざまな種類の双曲線、さらには双曲線に関する段階的な問題や演習も見つかります。
円錐曲線の一般方程式
各円錐曲線は方程式として解析的に表現できます。実際、すべての円錐方程式は 2 次でなければなりません。
したがって、係数の少なくとも 1 つは、
どちらか
式の値はゼロ以外でなければなりません。
したがって、パラメータ値に応じて、方程式はあるタイプの円錐曲線または別のタイプに対応します。
- 円周: 円周を記述する一般方程式の用語
そして
と一致する必要があります
ゼロでなければなりません。
- 楕円: 次の条件が検証されると、方程式は楕円の数式に対応します。
- 放物線: 方程式が放物線になるには、次の等式が満たされる必要があります。
- 双曲線: 最後に、双曲線の一般方程式は次の不等式を満たさなければなりません。
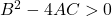投稿ナビゲーション