数値 Pi は、円の円周と直径の関係を表す数学定数です。無理数ですね。つまり、正確な分数ではありません。したがって、有限 10 進数として表すことはできません。 Pi の値は約 3.14159 で、ギリシャ文字の π で表されます。
円周率は数学において重要な数字です。したがって、さまざまな分野で多くの用途があります。たとえば、幾何学で面積を計算するために使用されます。また、円やその他の円形の図形の周囲。一方、三角法では円弧の角度と長さを計算します。最後に、工学および物理学において、体積や容量などの数量を計算します。
円周率の値 (3.14) に近いため、円周率の日は毎年 3 月 14 日に祝われます。この日付は、数学における円周率の役割を記念し、この基本定数への関心を促進するために祝われます。
円周率を発見したのは誰ですか?
円周率という数字は古代から知られており、それを正確に記述したのはギリシャの数学者アルキメデス (紀元前 287 ~ 212 年) でした。実際、彼はそれを幾何学的図形の面積と体積の計算に使用しました。
18 世紀、スイスの数学者ヨハン ランバートは円周率が無理数であることを証明しました。その後、19 世紀にドイツの数学者フェルディナント フォン リンデマンは、円周率が超越数であると説明しました。つまり、有理係数をもつ多項式の厳密な解として表すことはできません。
歴史を通じて、さまざまな数学者が円周率の理解に貢献し、円周率をより正確に計算する技術を開発してきました。今日でも、円周率は世界で最も重要かつ最もよく知られている数学定数の 1 つであり、数学の研究対象であり続けています。
なぜ円周率は無限なのでしょうか?
円周率の値は約3.14159ですが、実際には小数点以下無限に続く数値です。これは、Pi が無限の数であり、10 進数で完全に表すことができないことを意味します。
Pi の値は無限ですが、実際には、Pi の近似値は非常に正確に計算できます。これまでに、円周率の数百万桁が計算されており、円周率の 10 進数の桁には規則的なパターンがないことが示されています。とはいえ、そんなに多くの数字を計算することはできないので、これはスーパーコンピューターを介して行われました。
数値Piの近似値を計算するにはどのような方法がありますか?
円周率の値を計算するにはいくつかの実用的な方法がありますが、次に、数学者が最もよく使用する 3 つの方法を順を追って説明します。
1. アルキメデスの方法
ギリシャの数学者アルキメデスは、幾何学的な方法を使用して円周率の近似値を計算しました。この方法を使用するには、次の手順に従います。
1. 以下に示すように、円を描き、円の中心を通る線を引き、対向する 2 点で交差します。
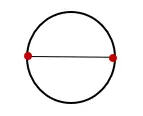
2. 円と交差する線の長さを測定し、「D」とラベルを付けます。この測定値は円の直径です。
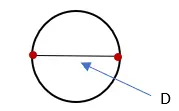
3. 円を形成する線の長さを測定し、「C」とラベルを付けます。この測定値は円の円周です。
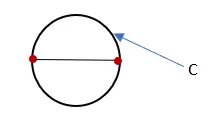
4. 円の円周 (C) を円の直径 (D) で割ります。結果は Pi の近似値です。
たとえば、円の直径が 6、円周が 18 の場合、円周率の近似値は 18 ÷ 6 = 3 です。明らかに、この例は非常に基本的なものですが、実際の円周の値を使用して実行すると、 , このメソッドが正しく機能することがわかります。
実際、これを試してみることをお勧めします。カップなどの円形のもののサイズを測って、それがうまくいくかどうかを確認してください。
2. モンテカルロ法
モンテカルロ法とは、平面上にランダムに多数の点を生成し、正方形に内接する円内に収まる点の数を数えることにより、円周率の近似値を計算する確率論的な手法です。このプロセスは次のように適用されます。
1. 以下に示すように、辺 1 の正方形の内側に円を描きます。

2. 正方形内に多数の点をランダムに生成します。
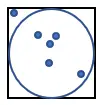
3. 円に収まる点の数を数えます。この数量を「n」と呼びます。
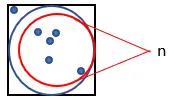
4. 生成されたポイントの総数をカウントします。この量を「m」と呼びます。
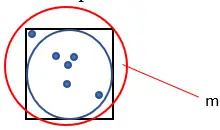
5. 次の式を使用して、Pi の近似値を計算します: Pi = (4 · n) ÷ m。
たとえば、380 個の点が生成され、300 個が円に収まった場合、Pi の近似値は (4 · 300) ÷ 380 = 3.16 となります。この値は、Pi の小数点以下 2 桁によく似ていますが、前の方法と同様に、実際の測定値を使用すると、さらに正確な値が得られます。
3. 反復法
反復法は、円周率の近似値を計算するために使用される数学的手法であり、円周率の値を暗黙的に示す式を使用し、繰り返し適用することで計算の精度を向上させます。この方法を使用する手順は次のとおりです。
- Pi の初期値を選択します。たとえば、値 3 を選択できます。
- Pi の値を含む式を使用して、新しい近似値を計算します。たとえば、次の式を使用できます。Pi = (Pi + (4 ÷ Pi)) ÷ 2
- 新しい近似値と古い値を比較します。 2 つの差が十分に小さければ、正確な結果が得られたことになります。差がまだ大きい場合は、新しい値を Pi に代入し、ステップ 2 からのプロセスを繰り返します。
たとえば、Pi の初期値が 3 の場合、新しい近似値は (3 + (4 ÷ 3)) ÷ 2 = 2.66666666 となります。ただし、2 つの間の差はそれほど小さいわけではないため、正確な値を見つける前にプロセスを何度か繰り返すことができます。
円周率という数字はどのような用途に使われるのでしょうか?
円周率は数学において重要な数値であり、さまざまな分野で多くの用途があります。 Pi の最も重要なアプリケーションには次のようなものがあります。
ジオメトリ
Pi は、円やその他の円形図形の面積と周長を計算するために幾何学で使用されます。
- 円: 円の面積と周囲長を計算します。
- 球: 球の面積と体積を決定します。
- 円柱: 円柱の表面積と体積を計算します。
- 円錐– 円錐の表面積と体積を計算するために使用されます。
三角法
三角法で角度と円弧の長さを計算するのに役立ちます。その応用例は次のとおりです。
- 角度: 角度と円弧の長さの計算。
- 三角関数– 特定の角度に対する三角関数の値を計算するために使用されます。
- 円三角法: 360 度の角度に対する三角関数の値を計算します。
エンジニアリング
工学では、Pi は体積や容量などの数量の計算に使用されます。その応用例は次のとおりです。
- 電子工学: 抵抗や静電容量などの量を計算します。
- 電気: 電力や電気エネルギーなどの量を計算するために使用されます。
- 土木工学: 構造物や建設要素の表面積や体積などの数量を計算します。
物理的な
数値 Pi (π) は、物理学で多くの用途に使用される数学定数です。物理学における Pi の使用例をいくつか示します。
- 波– 波の周波数と波長を計算するために使用されます。
- 力学: 力学では、回転系の仕事とエネルギーを計算するのに役立ちます。
- 電磁気学: 電磁気学では、コンデンサに蓄えられるエネルギーと巻線のインダクタンスを計算するために使用できます。
- 宇宙論 宇宙論では、時空の曲率と宇宙の膨張を計算するために円周率が使用されます。
円周率という数字は実生活でどのような用途に使われるのでしょうか?
Pi が日常生活でどのように使用されるかの例をいくつか示します。
- 幾何学: 円形マットの面積を定義するか、円形テーブルの周囲を覆うのに必要な巻尺の長さを測定します。
- 調理– 鍋を満たすのに必要な水や液体の量、または円形の容器に入る材料の数を決定します。
- 天文学: 惑星と星の間の距離、惑星の軌道、空の天体の位置を知ります。
- ガーデニング: 円形の鉢を満たすのに必要な土や土の量を知ったり、円形の庭で植物に水をやるのに必要な水の量を計算したりできます。