このページでは、割線の意味、存在するさまざまなタイプ、2 本の線が割線であるかどうかを知る方法、それらの共通点を見つける方法など、割線に関するすべてがわかります。また、いくつかの例と解決された演習も表示されます。割線の。
交差する2本の線とは何ですか?
数学における割線の定義は次のとおりです。
2 つの線が 1 点でのみ交差する場合、2 つの線は交差します。したがって、交差する線には共通点が 1 つだけあります。さらに、2 つの交差する線は必ず同じデカルト平面に含まれていなければなりません。
2 つの線が 1 点で交差するという概念は重要です。2 つの線に複数の交点があれば一致する線となり、一方、交点がなければ平行線となるからです。
交差する線の例
2 つの交差する線の意味を理解したら、次にこのタイプの線の 2 つの異なる例を見てみましょう。
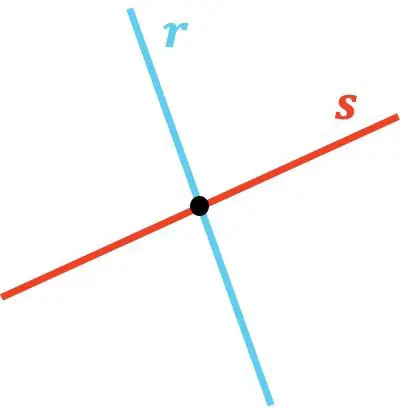
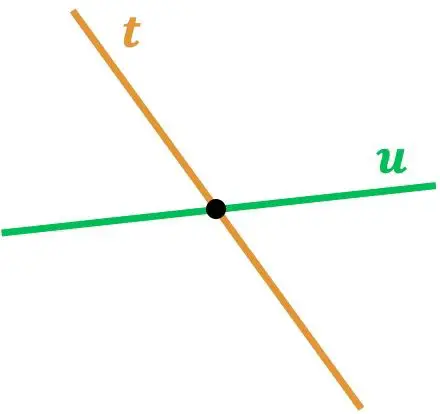
ご覧のとおり、直線rと直線 s は一点で接しているため交差します。そして、同様に、直線tと直線uが交わる点があるので、直線tと直線uが交差します。
交差する線の種類
交差する線には 2 つのタイプがあります。
- 垂直線: 90 度の直角で交差する線です。
- 斜線: 0 度から 90 度までの鋭角で交差する線で構成されます (含まれていません)。
垂直直線

垂直線は、 4 つの 90 度の角度を形成するように交差する線です。
同様に、2 つの垂線の傾きは常に次の条件を満たします。
![]()
垂直に交差する線のもう 1 つの特性は、それらの方向ベクトル (線の方向を示すベクトル) 間の内積が 0 に等しいことです。
![]()
垂直線にさらに興味がある場合は、このリンクで垂直線の例を参照できます。さらに、別の線に垂直な線を計算する方法、このタイプの線の特性、段階的に解決される演習なども説明します。
斜線

斜線は、鋭角と鈍角がペアになって交差する線です。つまり、2 つの鋭角 (90 度未満) と 2 つの鈍角 (90 度を超える) を作成します。ただし、2 つの線の角度の定義によれば、2 つの線の間の角度は、2 つの線がなす角度の中で最も小さいものになります。
2 本の斜線とその傾きの間の角度は、次の式を使用して計算できます。
![]()
2 本の線が交差しているかどうかはどうやってわかりますか?
2 つの直線の相対位置を求める方法は主に 3 つあります。
- 2 本の直線の方向ベクトルを使用します。
- 2本の線の勾配付き。
- 2 つの直線の暗黙的な (または一般的な) 方程式を使用します。
次に、2 つの線が交差するときを知るために存在する 3 つの方法について説明します。
線の方向ベクトルから
2 つの異なる線の方向ベクトル(線の方向を示すベクトル)の座標が比例しない場合、これら 2 つの線は交差します。
交差する 2 つの線を段階的に解決する演習を見てみましょう。
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=1+2t \\[2ex] y= 5-3t \end{cases}\qquad \qquad s: \ \begin{cases} x=1+t \\[2ex] y=2+4t \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5d8a2fa136f2840fc1f680e0f7f10ed6_l3.png)
両方の線はパラメトリック方程式として表現されるため、各線の方向ベクトルの成分はパラメータの前にある数値になります。
![]()
![]()
したがって、方向ベクトルが比例しているかどうかを確認するには、それらの座標をそれらの間で分割する必要があります。両方の部門で同じ結果が得られた場合、それらは比例します。一方、結果が異なる場合は、ベクトルが比例していないことを意味します。
![]()
コンポーネントの分割は等価ではないため、ベクトルは比例せず、したがって線は交差します。
坂の始まりで
2 本の線の傾きが異なる場合、これは線が交差していることを意味します。
たとえば、次の 2 つの線は、傾きが異なるため交差します。
![]()
線の傾き
![]()
-2 と直線の傾き
![]()
は3です。
![]()
2 つの線は同じ傾きを持たないため、交差します。
直線の暗黙的な方程式から
また、2 つの直線が交差するかどうかは、直線の陰的な方程式 (または一般方程式) によって知ることができます。直線の暗黙的な方程式は次のとおりです。
![]()
したがって、係数 A と B が比例しない場合、2 つの直線は交差します。
暗黙的な方程式で定義された 2 つの交差する線の例を見てみましょう。
![]()
これらが 2 つの交差する線であることを検証するには、係数 A (変数の前の数値) の比例性を分析する必要があります。
![]()
) 係数 B (変数の前の数字)
![]()
):
![]()
2 つの項は比例しないため、実質的に 2 つの線は交差します。
2本の交差する線の共通点を見つける
これまで見てきたように、交差する線には共通点が 1 つだけあります。したがって、2 つの割線の交点を計算するには、2 つの直線によって形成される連立方程式を解く必要があります。
例として、次の 2 つの線の交点を見つけます。
![]()
2 つの直線の交点を決定するには、2 つの直線によって形成される連立一次方程式を解く必要があります。
![Rendered by QuickLaTeX.com \left.\begin{array}{l} x+2y-5=0\\[2ex] 2x-3y+3=0\end{array}\right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-77ae257986963d3652d5996fc09be9fb_l3.png)
この場合は代入法で系を解きます。したがって、変数を分離します
![]()
最初の式から得た値を 2 番目の式に代入します。
![Rendered by QuickLaTeX.com \left.\begin{array}{l} x+2y-5=0\\[2ex] 2x-3y+3=0\end{array}\right\} \begin{array}{l}\longrightarrow \ x=5-2y \\[2ex]&\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3ad955c3f2ebeb8ad0bdee85a226c73b_l3.png)
![]()
![]()
![]()
![]()
![]()
そして、未知のものにどれだけの価値があるかがわかれば、
![]()
その値を、見つかった式に代入します。
![]()
![]()
![]()
したがって、連立方程式の解は 2 つの直線の交点になります。そしてこのポイントは、
![]()
円と交差する線
通常、2 本の線が交差すると言うとき、先ほど見た概念を指します。ただし、幾何学では割線には別の意味があります。
円と交差する線は、 2 つの異なる点で円 (または曲線) と交差する線です。
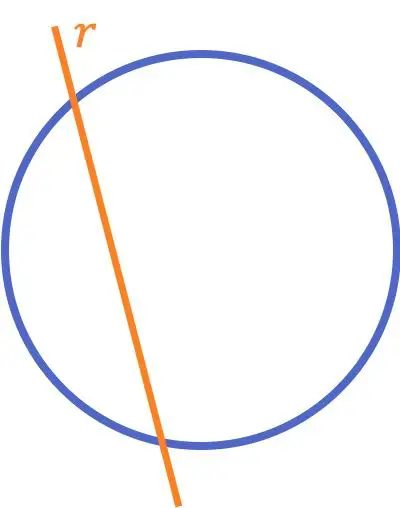
通常小学校で教えられる 2 つの交差する線の概念とは異なり、円と交差する線のこの定義は、線と円のすべての相対位置とともに後の授業で学習されることがよくあります。