二次方程式または二次方程式は、次数 2 の方程式であり、その項の 1 つの最大指数が 2 に等しくなります。これは、方程式には最大 2 つの異なる解が存在する可能性があることを意味しますが、一意の解または固有の解が存在する場合もあります。まったくありません。
二次方程式の解または根を計算するには、二次公式を使用するか、式を因数分解するという 2 つの異なる手順に従うことができます。この記事では、両方の方法について説明し、いくつかの実践的な演習を行います。ただし、その前に、説明全体がよく理解され、読書を最大限に活用できるように、いくつかの概念を明確にします。
二次方程式の種類
二次方程式間の主な分類は、式自体の構造に基づいています。したがって、これらの式の標準または通常の構造は次のとおりです: ax² + bx + c 。この一般的な形式は完全な方程式と同等ですが、null または null 項がある場合、構造が変化する可能性があり、不完全な方程式が表示されます。次に、各タイプの特徴を詳しく説明します。
完全な二次方程式
すでに述べたように、完全な 2 次方程式があり、これらの係数 a、b、c はすべてゼロではありません。したがって、式には二次項、一次項、独立項のすべての項があるため、この式は ax² + bx + c という構造を文字どおりに従います。このタイプの例は、次の方程式です: x² + 2x + 1 = 0。
不完全な二次方程式
不完全な方程式については、どの係数がゼロに等しいかによって区別できます。この説明で疑問が解決しない場合は、以下の画像ですべてのケースを段階的に説明してください。
- 不完全方程式 (b = 0):この最初の状況では、ax² + c = 0 という構造に従う式が見つかります。これにより、分数 c/a の根の負と正の 2 つの結果が得られます。 。
- 不完全方程式 (c = 0): ax² + bx = 0 の形式がある場合、式 x (ax + b) = 0 になるように方程式を因数分解する必要があります。したがって、x = 0 と x = – の 2 つの解が得られます。 b/a。
- 不完全方程式 (b = c = 0):この場合、方程式 ax² = 0 があり、可能な解は 1 つだけあり、それは x = 0 です。
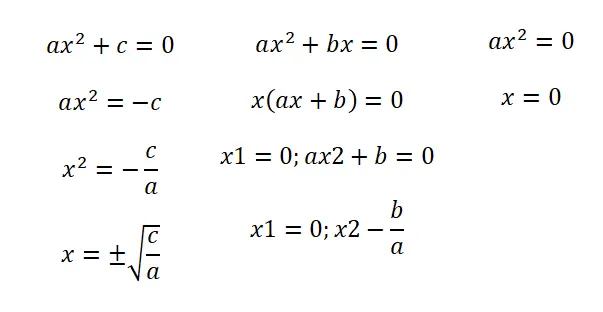
私たちが教えた手順を使用すると、不完全な方程式を解くときにより速く進めることができることは言及する価値があります。しかし、どのような場合でも、以下で説明する二次公式を使用することができ、存在しない係数にゼロを書き込むだけで済みます。
二次方程式の公式
二次方程式(ax² + bx + c = 0)を解くには、一般公式または二次公式を適用し、数式内の各文字に対応する数値を代入する必要があります。
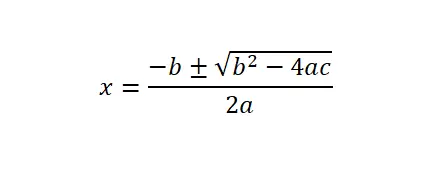
また、判別式 (Δ) は平方根の下にある式 b² – 4ac であることを説明することが重要です。この数学的概念から、この二次方程式の解がいくつあるかを知ることができます。基本的に、判別式が負である (実際の解が存在しない)、判別式がゼロである (解が 1 つだけある)、または判別式が正である (解が 2 つある) という 3 つのオプションがあります。
完全な二次方程式を解く例
次の二次方程式2x²+4x-6=0を解いてみて、結果を以下の式で確認してください。次の手順に従うことをお勧めします: 方程式のタイプを分析し (ゼロ項を特定)、判別式を計算して既存の解の数を知り、最後に提案された方程式をその公式で解きます。
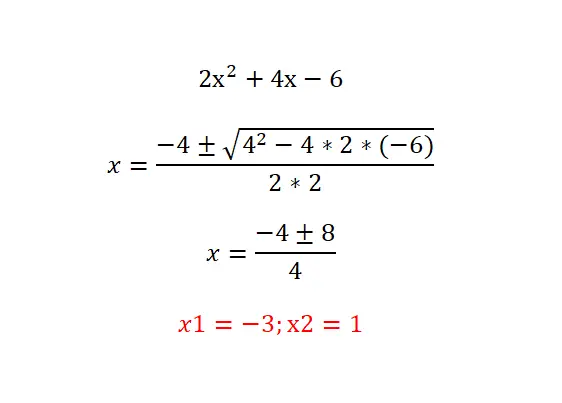
階乗二次方程式
二次方程式を解くための 2 番目の方法は因数分解です。したがって、多項式 (この場合は 2 次多項式) を因数分解するには、さまざまな方法を使用できます。ただし、この形式の方程式に関しては、通常、共通の項で因数分解できます。そうでない場合は、 Notable Identitiesを適用してみることもできますが、通常、このような状況では他の方法を知る必要はありません。
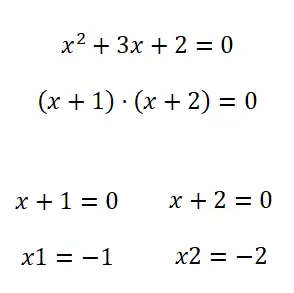
二次方程式の解を使った演習
以下に、完全および不完全な 2 次方程式に関する一連の演習を示します。こうすることで、この記事全体で説明されているすべての理論を確認することができ、それを演習に適用する方法がより明確になります。問題を自分で解決しようとして、問題を完了した場合、または行き詰まった場合にのみ解決策を見ることをお勧めします。とはいえ、今から演習を解き始めることができます。
演習 1
次の二次方程式を解きます。
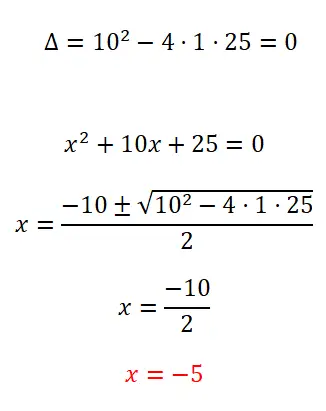
- 考えられる解の数を知るために、判別式を計算することから始めます。
- これは完全な二次方程式なので、二次方程式を適用して計算を解きます。
- 未知の x の値を取得します。
演習 2
次の二次方程式を解きます。
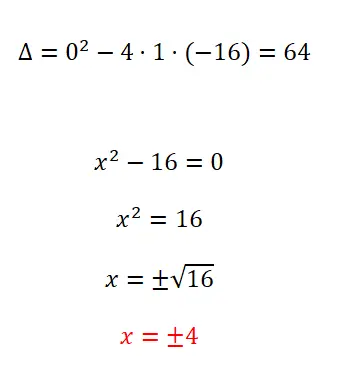
- まずは判別式を計算することから始めます。
- b = 0 の不完全な 2 次方程式があるため、このタイプの方程式に標準を適用します。
- 計算を解いて結果を求めるのですが、±記号を忘れてはいけません。
演習 3
次の順序なし 2 次方程式を解きます。
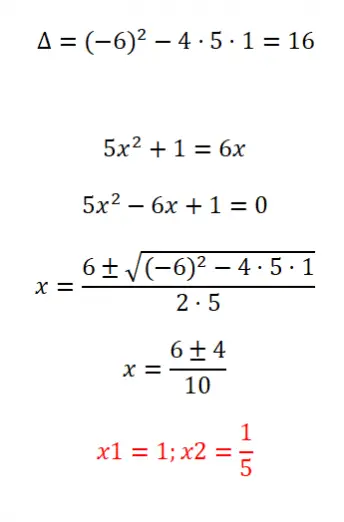
- まず、方程式の判別式を計算します。
- 式を適用する前に、ax² + bx + c = 0 の構造に従って方程式を順序付ける必要があります。
- 次に、一般式を適用します。
- そしてついに結果が得られます。
演習 4
次の二次方程式を因数分解して解きます。
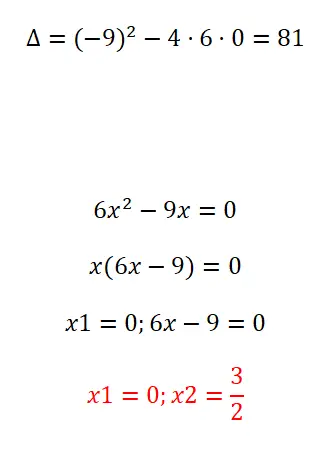
- まず判別式を計算します。
- 次に、x の共通因数を抽出します。
- したがって、最初の解は x = 0 です。
- そして2番目はx = 3/2です。
演習 5
以下に示す完全な 2 次方程式を解きます。
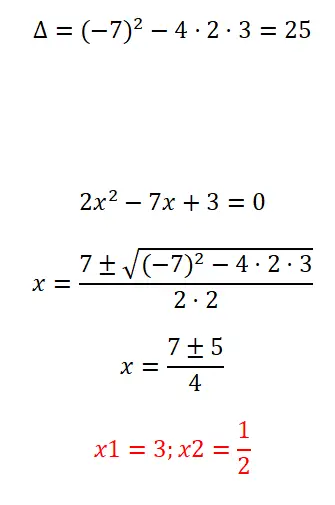
- いつものように、判別式を計算して、問題の方程式に解がいくつあるかを調べます。
- 次に、二次公式は完全な方程式であるため、二次公式を適用します。
- 最後に、方程式の結果を表します。
演習 6
私たちが提供する分数を使用して二次方程式を解きます。
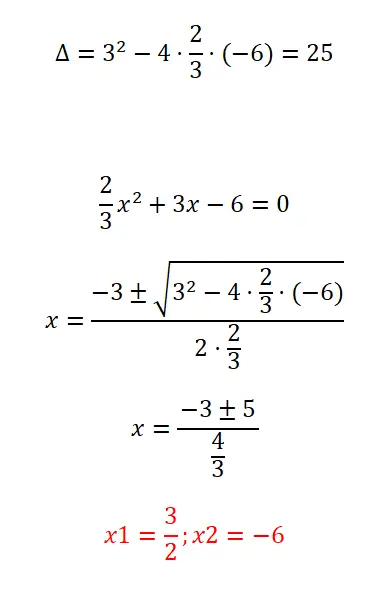
- まず、式の判別式を計算します。
- 次に、係数「a」が分数であることを考慮して、2次公式を適用します。
- 計算を解きます。
- そして方程式の 2 つの根はすでに得られています。
演習 7
次の二次方程式を解きます。
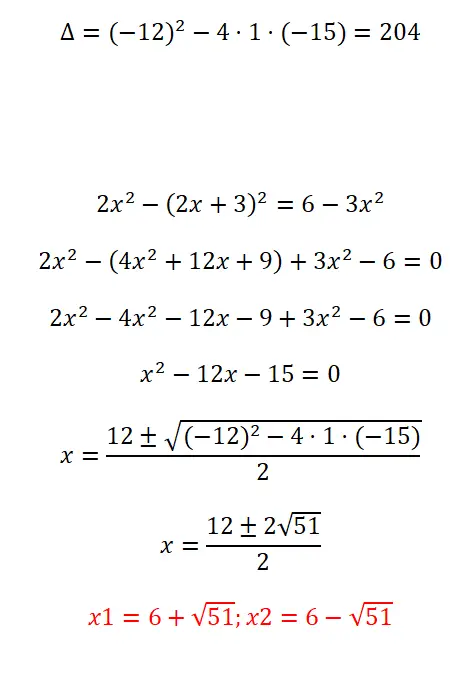
- まずは判別式を計算することから始めます。
- 式を適用する前に、式を簡略化し、ax² + b + c = 0 の形式にする必要があります。
- 式内のすべての係数を代入して計算を解きます。
- 最後に結果が得られます。
演習 8
次の二次方程式を解く証明:
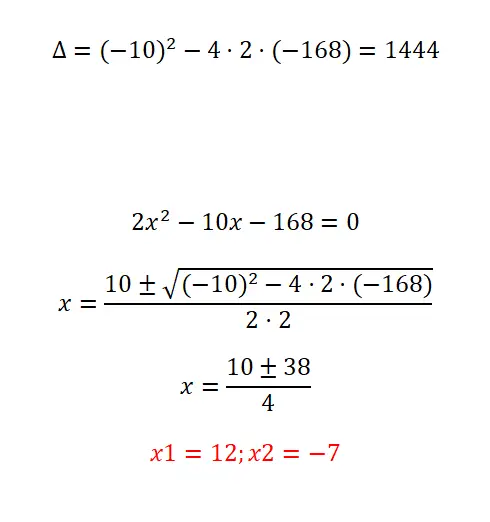
- まずは判別式を計算することから始めます。
- ご覧のとおり、これは単純な二次方程式ですが、非常に大きな係数があります。したがって、計算式を適用し、操作を実行するときは注意する必要があります。
- 最終的には両方の可能な解決策が得られます。