このページでは、二次関数とは何か、またそのすべての特性 (曲率、頂点、軸との交点など) について説明します。また、グラフ上で二次関数を表現する方法も学びます。最後に、二次関数に関する例、段階的な演習、問題を使って練習することができます。
二次関数とは何ですか?
二次関数の定義は次のとおりです。
数学では、二次 (または放物線) 関数は 2 次の多項式関数、つまり、最高次項が 2 次である関数です。したがって、二次関数の公式は次のようになります。
![]()
金:
-
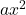
は二次項です。
-
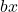
は線形項です。
-

は独立した用語です。
二次関数の定義域は常に実数で構成されます。
![]()
二次関数の凹凸
二次関数または放物線関数の曲率の解析は、二次関数の係数のみに依存するため、非常に簡単です。
- 係数が

が正の場合、二次関数は凸です (次の形式)

)。したがって、サミットは最低限のものです。
- 係数が

が負の場合、二次関数は凹型になります (次のような形状になります)

)。したがって、ピークは最大値です。


注:数学界はまだ完全に同意していないため、一部の教授は反対のことを言っています。彼らは、関数の形状を凹型関数と呼びます。
![]()
、および次の形式を持つ凸関数
![]()
。いずれにせよ、名前が何であれ、重要なのはどのような形状に機能があるかです。
二次関数の頂点
二次関数をグラフ化するには、放物線の頂点の座標を知る必要があります。
二次関数の頂点を見つけるには、次の式を使用して点の X 座標を計算する必要があります。
![]()
次に、その点での関数のイメージを計算することで、他の頂点座標を見つけることができます。
![]()
したがって、二次関数 (または放物線) の頂点の座標は次のようになります。
![]()
二次関数の軸で点を切断する
放物線は常に Y 軸 (Y 軸) と交差します。これは次の場合に発生します。
![]()
したがって、Y 軸を使用した 2 次関数のカットオフ点を計算するには、次のことを解決する必要があります。
![]()
たとえば、次の二次関数の OY 軸との交点は次のとおりです。
![]()
![]()
![]()
一方、x 軸 (X 軸) を持つ 2 次関数のカットオフ点は、次の場合に発生します。
![]()
したがって、X 軸との交点を計算するには、次の方程式を解く必要があります。
![]()
例として、同じ二次関数の OX 軸を使用したカットオフ点の計算を以下に示します。
![]()
![]()
次の一般式を使用して二次方程式を解きます。
![]()
![]()
したがって、二次関数と X 軸の交点は次のようになります。
![]()
この場合、二次方程式の解は 1 つしか得られませんでしたが、2 つの解が得られる可能性もあります。この場合、二次関数が 2 つの異なる点で X 軸と交差することを意味します。
二次関数または放物線関数の表現例
例を使用して、グラフ上で2 次関数を表す方法を見てみましょう。
- 次の関数をグラフ化します。
![]()
最初に行うことは、放物線の頂点を計算することです。これを行うには、上で見た式を使用します。
![]()
頂点がどこにあるかがわかったら、値のテーブルを作成する必要があります。 頂点とその周囲の点における関数の値を計算します。
![]()
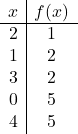
放物線をより適切に描画するために、デカルト軸を使用して 2 次関数のカット ポイントを計算することもできますが、これは厳密に必要なわけではありません。
得られた点をグラフ上に表現します。
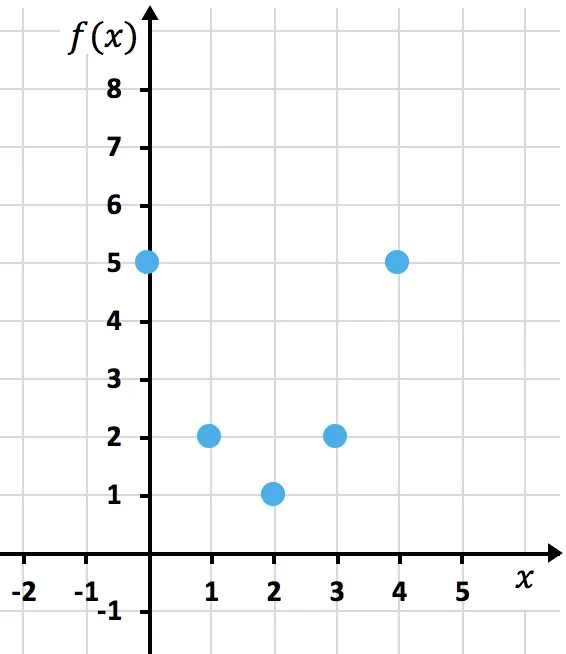
そして最後に、放物線を形成する点を結合します。次に、放物線が上向きに続いていることを示すために、放物線の枝を長くします。

二次関数の演習問題を解決しました
演習 1
次の二次関数の頂点を見つけます。
![]()
まず、次の式を使用して頂点の X 座標を計算します。
![]()
そして、その点で関数を評価して他の座標を計算します。
![Rendered by QuickLaTeX.com \begin{aligned} f(-2) & =2(-2)^2+8(-2)+4 \\[1.7ex] & = 2 \cdot 4 - 16 +4 \\[1.7ex] & = 8-16+4 \\[1.7ex] & = -4 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d6067325564a5af06f7384d76157f3aa_l3.png)
したがって、二次関数の頂点は次のようになります。
![]()
演習 2
軸を使用して次の関数のカットオフ点を見つけます。
![]()
Y 軸でカットポイントを計算するには、次のように計算する必要があります。
![]()
![]()
したがって、関数は次の点で Y 軸を通過します。
![]()
そして、X 軸でカットポイントを見つけるには、解決する必要があります。
![]()
![]()
![]()
次の式を使用して二次方程式の根を計算します。
![]()
![Rendered by QuickLaTeX.com \displaystyle x=\cfrac{-(-4)\pm \sqrt{(-4)^2-4\cdot 1\cdot 3}}{2\cdot 1} =\cfrac{4\pm 2}{2} = \begin{cases} 3 \\[2ex] 1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0d909ba6581faf5916f0b1c0df7e471f_l3.png)
したがって、関数は次の 2 点で X 軸を切断します。
![]()
演習 3
次の二次関数をグラフにします。
![]()
これは二次関数です。したがって、これを表すには、まず次の式を使用して放物線の頂点の横座標を計算する必要があります。
![]()
次に、値のテーブルを作成します。これを行うには、次の値を計算します。
![]()
上部と上部付近:
![]()
![]()
![]()
![]()
![]()
最後に、グラフ上に点をプロットし、放物線を描きます。

演習 4
次の二次関数をグラフにします。
![]()
これは二次関数です。したがって、これを表すには、まず次の式を使用して放物線の頂点の横座標を見つける必要があります。
![]()
次に、値のテーブルを作成します。これを行うには、次の値を計算します。
![]()
上部と上部付近:
![]()
![]()
![]()
![]()
![]()

最後に、グラフ上に点をプロットし、放物線を描きます。

演習 5
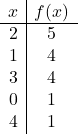
次の不完全な 2 次関数をグラフにプロットします。
![]()
これは 2 次の多項式関数です。したがって、これを表すには、まず次の式を使用して放物線の頂点の横座標を計算する必要があります。
![]()
この場合、関数には 1 次項がないため、関数は不完全です。そのために
![]()
次に、値の表を作成します。これを行うには、次の値を計算します。
![]()
上部と上部付近:
![]()
![]()
![]()
![]()
![]()

最後に、グラフ上に点をプロットし、放物線を描きます。

演習 6
二次関数に関連する次の問題を解きます。
製品の製造コストは次の関数で定義されます。
![]()
金
![]()
生産される単位 (千単位) および
![]()
はユニットの製造コスト (単位は数千ユーロ) です。
- 生産コスト関数をグラフで表します。
- コストを最小限に抑えるために、何千個のユニットを生産する必要があるかを決定します。
これは二次関数です。したがって、これを表すには、まず次の式を使用して放物線の頂点の横座標を見つける必要があります。
![]()
次に、値の表を作成します。これを行うには、次の値を計算します。
![]()
上部と上部付近:
![]()
![]()
![]()
![]()
![]()
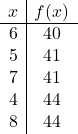
次に、グラフ上に点をプロットし、放物線を描きます。
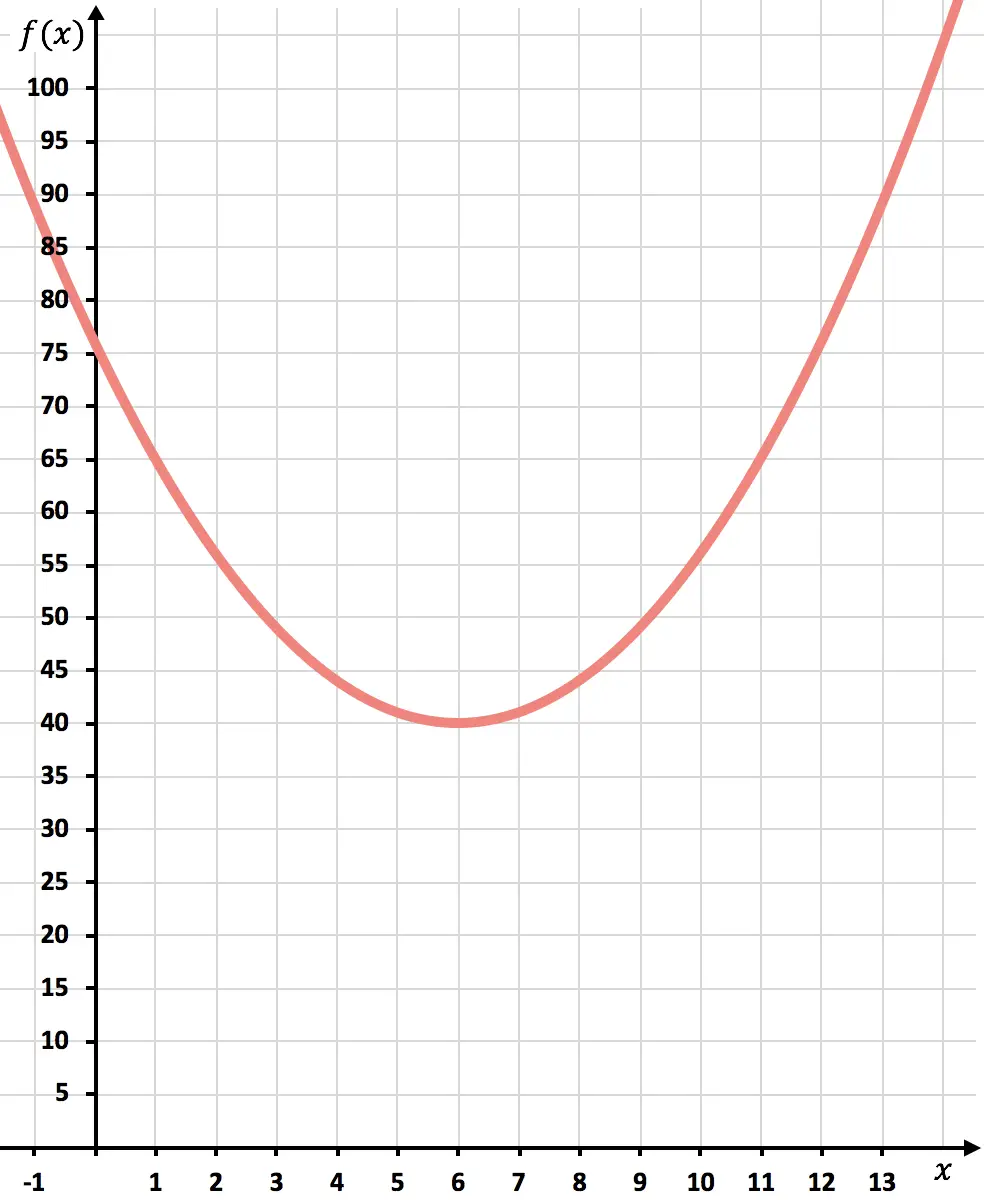
関数が表現されたら、コストがどれだけ最小化されるかを確認します。
グラフが示すように、最小コストは放物線の頂点に達します。それは関数が最小値を取る場所だからです。
結論として、6,000 個生産することでコストは最小限に抑えられます。
演習 7
次の二次関数の問題を解きます。
アスリートがやり投げを実行すると、その軌道は次の関数で表すことができます。
![]()
金
![]()
やり投げでカバーされるメートルと
![]()
その高さ(メートル単位でも)。
やり投げが到達できる最大の高さはどれくらいですか?
これは二次関数なので、槍の軌道は放物線になります。
また、二次項の係数が負(-0.025)であるため、放物線は逆U字型となり、枝が下に向かっていきます。したがって、投げ槍は頂点で最大の高さに達します。これは、これが放物線の最高点となるためです。
したがって、放物線の頂点の横座標を次の式で計算します。
![]()
そして、次の関数を評価して、その時点でやり投げがどのくらいの高さになるかを計算します。
![]()
![]()
したがって、やり投げが到達できる最大の高さは 42 メートルです。
演習 8
二次関数に関する次の問題を解いてください。
企業の生産コスト (ユーロ単位) は、次の関数によって定義されます。
![]()
金
![]()
生産されたユニットです。
そして、各ユニットの販売価格は520ユーロです。
- 150 個販売すると、会社はどれくらいの利益を得ることができますか?
- 最大の利益を得るには何ユニット販売する必要がありますか?
同社は販売ユニットごとに 520 ユーロの収入を得ます。したがって、収入を定義する関数は次のようになります。
![]()
金
![]()
販売単位です。
しかし、彼らは利益、つまり収入からコストを差し引いたものについて尋ねます。したがって、収益からコストを差し引いて、会社の利益を表す関数を取得します。
![]()
![]()
![]()
![]()
会社の利益を表す関数がわかったら、関数式に 150 を代入して、会社が 150 個販売することで得られる利益を計算します。
![Rendered by QuickLaTeX.com \begin{aligned} B(150) & =-(150)^2 + 500\cdot 150 - 40000 \\[2ex] & = -22500+75000 - 40000 \\[2ex] & = \bm{12500} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9f5e6f3101145bcf1a2ece4db3e07c4e_l3.png)
したがって、150 個販売すると、会社は 12,500 ユーロの利益を得ることができます。
このステートメントでは、最大利益が達成されるユニット数を計算するよう求められています。
利益を表す関数は 2 次関数なので、放物線の形状になります。また、二次項の係数は負(-1)なので、放物線は逆U字型となり、枝は下に伸びます。したがって、放物線の最高点である上部で最大のゲインが得られます。
したがって、放物線の頂点の横座標を次の式で計算します。
![]()
したがって、会社は 250 個販売することで最大の利益を得ることができます。
一方、プレスリリースで要求されていなくても、これら 250 ユニットの販売によって得られる利益を決定できます。
![]()
ユーロ