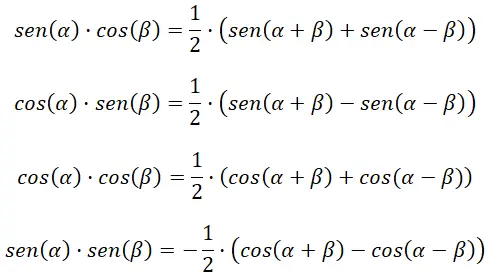三角恒等式は、異なる三角関数間の等式です。これらの三角比の等価性のおかげで、他の三角比に基づいて特定の三角比を推定することができます。したがって、三角恒等式の公式を理解するには、これらの比の公式を知る必要があります。あなたのケースでそれらがわからない場合は、最後のリンクにアクセスすることをお勧めします。
三角恒等式の表
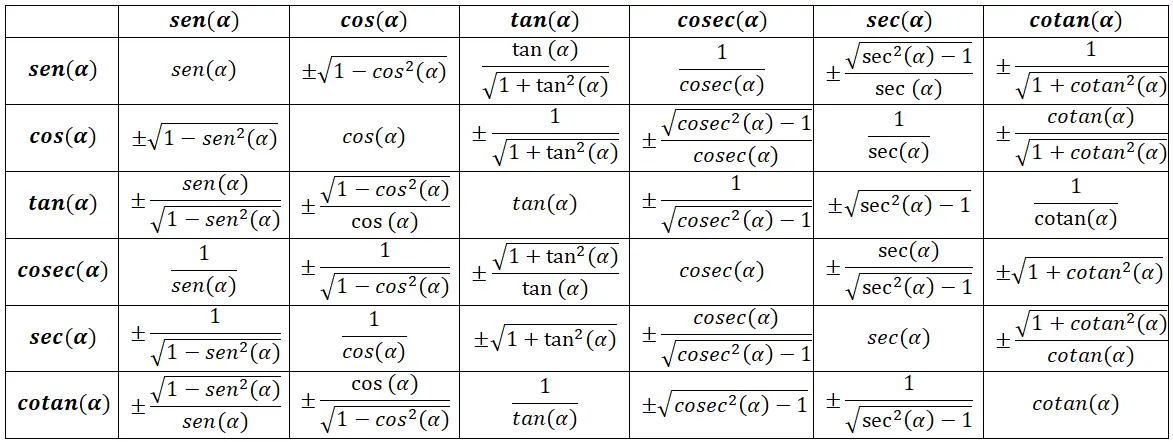
基本的な三角恒等式
一連の基本的な三角恒等式があり、それらは他の恒等式の理論的基礎を提供するため、最も重要であると考えられています。これらは最も一般的であり、非常に直感的であるため、おそらく最も覚えやすいものです。すべての数式は次の画像に基づいていることに注意してください。

基本的な三角関数の恒等式
すべての最初の恒等式は、基本三角関数恒等式として知られているもので、サインとコサインの関係としても知られています。以下はその数学的証明です: sin² (α) + cos² (α) = 1。
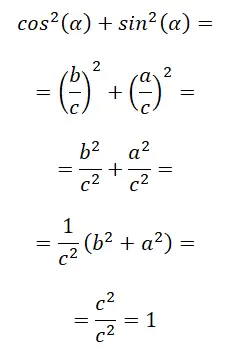
最後のステップでは、基本的にピタゴラスの定理を適用します。c² = a² + b² であるため、c² / c² は 1 に等しくなります。結論として、次のように言えます。 sin² (α) + cos² (α) = 1。
セカントとタンジェント(セカントの二乗)の関係
次に、セカントをタンジェントに関連付ける三角関数の恒等式が得られます。その式は次のとおりです: sec² (α) = 1 + Tan² (α) 。次の図では、このアイデンティティを構成するいくつかのリマインダー式と、最終的な式に到達するまでの手順を示しています。
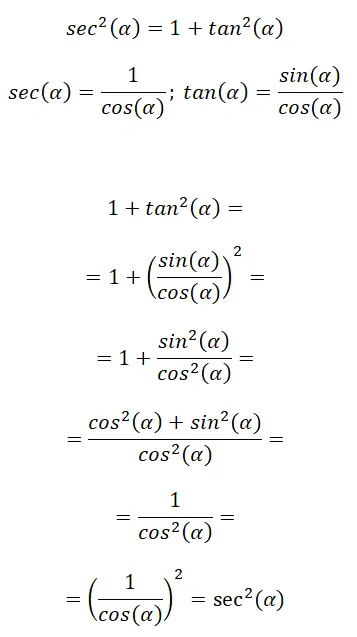
この場合、三角比の式を使用して他の比を求めます。結論として、sec²(α) = 1 + Tan²(α) と言えます。
コセカントとコタンジェント(コセカントの二乗)の関係
コセカントとコタンジェントの定義から、タンジェントの公式にリンクを見つけることができます。このおかげで、別の三角関数恒等式、 cosec² (α) = 1 + cotg² (α) を推定できます。
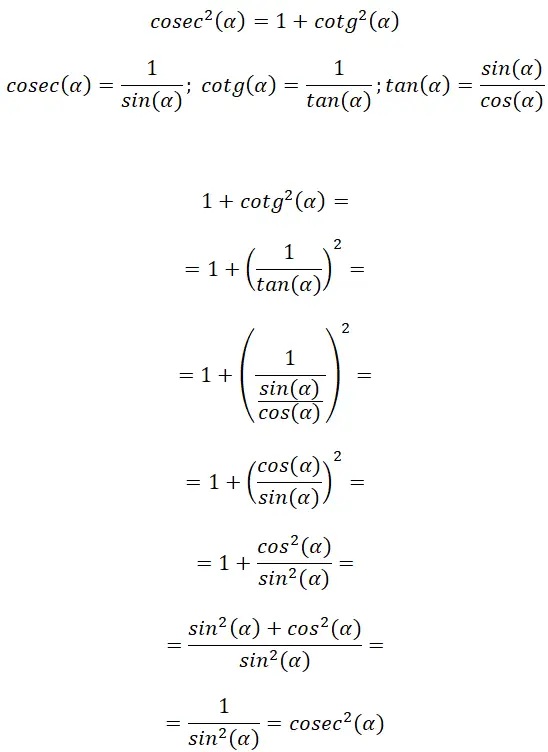
このデモでは、cosec² (α) = 1 + cotg² (α) であることを確認できます。さらに、この関係は前の関係とある程度の類似性があることがわかります。これは、接線と余接が類似しているためです。
和角と減算角の三角比
角度の和または減算の比は、 2 つの角度の加算または減算の三角比を計算することによって得られる恒等式の一種です。たとえば、90 + 60 のサインを計算したい場合、この計算を簡単にする一連の公式があります。以下は、このスタイルの三角恒等式のすべての公式のリストです。
角度の合計のサイン: sin (α + β ) = sin (α) cos ( β ) + cos ( α ) sin ( β )
角度減算の正弦: sin (α – β ) = sin (α) cos ( β ) – cos ( α ) sin ( β )
角度の合計のコサイン: cos (α + β ) = cos (α) cos ( β ) – sin ( α ) sin ( β )
角余弦の減算: cos (α – β ) = cos (α) cos ( β ) + sin ( α ) sin ( β )
角度の合計の正接: Tan (α + β ) = (tan (α) + Tan ( β )) ÷ (1 – Tan (α) Tan ( β ))
角正接の減算: Tan(α – β ) = (tan(α) + Tan( β )) ÷(1 + Tan(α)tan( β ))
150°の正弦を計算する方が、先ほど説明した式を使用して (90° + 60°) の正弦を計算するよりも簡単であることは明らかです。では、なぜこれらの公式が重要なのでしょうか?答えは、これらの恒等式を使用すると、より単純な角度から複雑な角度の三角比を計算できるようになります。したがって、注目すべき(最も関連性の高い)角度の比率を記憶しておけば、150 度などのより複雑な角度の比率を計算するために電卓を使用する必要がなくなります。
倍角三角比
倍角 (2α) の三角比を計算したい場合、一連の恒等式を使用して計算できます。より正確には、前のセクションで説明したものと非常によく似た数式を通じてこれを行うことができます。 βを α に変更すると、前の式では (α + α) が残り、これは (2α) に相当します。これを念頭に置くと、次の恒等式を導き出すことができます。
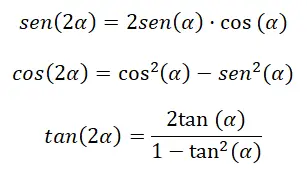
以下のデモを見ることができます。
倍角の正弦: sin (2α) = sin (α) cos (α) + cos (α) sin (α) = 2 sin (α) cos (α)
倍角の余弦: cos (α + α ) = cos (α) cos ( α ) – sin ( α ) sin ( α ) = cos² (α) – sin² (α)
二重接線角度:tan (2α) = 2 Tan (α) ÷ (1 – Tan² (α))
半角の三角比
また、半角 (α/2) の三角比を計算できる恒等式もあります。
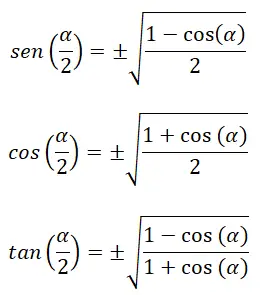
すでに知られている式としては次のようなものがあります。
1 = sin²( β ) + cos²( β )
cos( 2β ) = cos²( β ) – sin²( β )
β = α/2 とすれば、サインの場合は 2 つの式を引き、コサインの場合は足し、得られた 2 つの式 (サインとコサインの式) を割ることで、これらの恒等式を証明できます。タンジェントの場合。ただし、以下で得られる式で計算したい比率を分離することが残っています。
正弦半角: 1 – cos (α) = 2 sin² (α/2); sin² (α/2) = (1 – cos (α)) ÷ 2
半角余弦: 1 + cos (α) = 2 cos² (α/2); cos² (α/2) = (1 + cos (α)) ÷ 2
三重角の三角比
三重角 (3α)がある場合、特定の恒等式を使用して三角比を計算することもできます。これらの恒等式は、既に説明した次の公式、つまり倍角の恒等式、和角の恒等式、および三角法の基本的な恒等式から得られます。
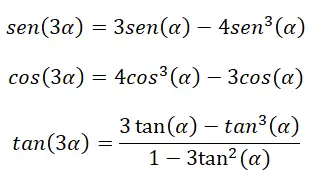
これらの同一性を証明するには、角度の合計の公式を使用する必要があります。
角度の合計の正弦: sin (3α) = sin (α + 2α) = sin (α) cos (2α) + sin (2α) cos (α)
角度の合計のコサイン: cos (3α) = cos (α + 2α) = cos (α) cos (2α) – sin (α) sin (2α)
したがって、今話した式に倍角の公式を適用し、三角法の基本的な恒等式を適用すれば、恒等式を証明することができます。基本的な三角関数の恒等式を使用すると、式内のすべての比率を 1 つに変換できることに言及する価値があります。三重角のサインの公式がサインのみで構成され、コサインの公式がコサインのみを含むのはこのためです。以下に完全な手順を示します。
3 倍角の正弦: sin (3α) = sin (α + 2α) = sin (α) cos (2α) + sin (2α) cos (α) =
= sin (α) (cos² (α) – sin² (α)) + 2 sin (α) cos (α) cos (α) =
= sin (α) cos² (α) – sin³ (α) + 2 sin (α) cos² (α) =
= sin (α) · (1 – sin² (α)) – sin³ (α) + 2 sin (α) · (1 – sin² (α)) =
= sin (α) – sin3 (α) – sin3 (α) + 2 sin (α) – 2 sin3 (α) =
= 3 sin (α) – 4 sin3 (α)
3 倍角の余弦: cos (3α) = cos (α + 2α) = cos (α) cos (2α) – sin (α) sin (2α) =
= cos (α) (cos² (α) – sin² (α)) – sin (α) 2 sin (α) cos (α) =
= cos3 (α) – cos (α) sin² (α) – 2 cos (α) sin² (α) =
= cos3 (α) – 3 cos (α) sin2 (α) =
= cos3 (α) – 3 cos (α) · (1 – cos2 (α)) =
= cos3 (α) – 3 cos (α) + 3 cos3 (α) =
= 4 cos3 (α) – 3 cos (α)
最後に、 3 倍角の正接は2 つの方法で計算できます。1 つ目はサイン公式をコサイン公式で割る方法で、2 つ目は 2 倍角のタンジェントの式を次の式に代入して次の式に代入します。合計角度: Tan (α + 2α) = (tan (α) + Tan (2α)) ÷ (1 – Tan (α) Tan (2α))。
角度の種類に応じた三角恒等式
三角比の直接かつ迅速な計算を可能にするある意味ルールである一連の公式についてコメントすることが重要です。実際、これらは今説明したすべての式と同じ特性を満たすため、三角恒等式とみなすこともできます。より正確には、これらの公式を使用すると、ある角度と別の角度との関係から、その角度の三角関係を判断できます。
補角
補角(α とβ ) は合計が 90 度に等しいため、それらを加算すると直角が得られます。 α がβの補角であることを確認するには、非常に単純な方程式 α = 90 – βを解く必要があります。この等価性の結果が一致する場合、それらが相補的であると断言できます。これらの恒等式のおかげで、ある角度の三角比を他の角度の三角比から推定することができます。
余角のサイン:sin (90° – α) = cos (α)
余角の余弦: cos (90° – α) = sin (α)
補角の正接:tan(90° – α) = cotan (α)
補角のコセカント: cosec (90° – α) = sec (α)
余角の正割: sec (90° – α) = cosec (α)
補角の余接: cotan (90° – α) = Tan (α)
追加の角度
補助角(α とβ ) は、合計が 180° または π ラジアンに等しい角度であるため、式 α + β = 180° を推定できます。つまり、α の補角をβとすると、次式β = 180 – αを満たす必要があります。次に、これらの角度から推定できるアイデンティティのリストを確認できます。
補角の正弦:sin (180° – α) = sin (α)
追加角の余弦: cos (180° – α) = -cos (α)
補助角の正接:tan (180° – α) = -tan (α)
追加角のコセカント: cosec (180° – α) = cosec (α)
補助角の正割:sec (180° – α) = -sec (α)
補角の余接: cotan (180° – α) = -cotan (α)
共役角
共役角(α とβ ) は、合計が 360° または 2π ラジアンに等しい角度です。これが、式 α + β = 360° を推定できる理由です。この最初の式から、一方の角度をもう一方の角度で次のように表すことができます: α = 360° – βまたはβ = 360° – α。ここで、共役角の等式を示します。
共役角のサイン: sin (360° – α) = – sin (α)
共役角の余弦: cos (360° – α) = cos (α)
共役角の正接:tan (360° – α) = – Tan (α)
共役角のコセカント: cosec (360° – α) = – cosec (α)
共役角の正割: 秒 (360° – α) = 秒 (α)
共役角の余接: cotan (360° – α) = – cotan (α)
反対の角度
反対の角度または負の角度(α とβ ) は、数値は同じですが、符号が異なります。このタイプの角度の例は、30 度と -30 度です。負の符号は回転が時計回りであることを示し、正の角度は反時計回りに回転することを覚えておいてください。
逆の角度の正弦: sin (-α) = – sin (α)
反対角の余弦: cos (-α) = cos (α)
対角の正接:tan (-α) = – Tan (α)
反対角のコセカント: cosec (-α) = – cosec (α)
逆角の正割:sec(-α) = sec(α)
反対角の余接: cotan (-α) = – cotan (α)
90°以外の角度、または角度プラス/マイナスπ/2
90 度異なる角度、または角度プラス/マイナス π/2 (α およびβ ) は、90 度の差がある角度です。したがって、これらはβ – α = 90° として表すことができます。ここで、 βはαより 90° 大きくなります。これらの角度には、2 つの角度の三角比を関連付ける一連の公式もあります。
90°とは異なる角度のサイン:sin (90° + α) = cos (α)
90°とは異なる角度の余弦: cos (90° + α) = -sin (α)
90°とは異なる角度の正接:tan (90° + α) = – cotan (α)
90°とは異なる角度のコセカント: cosec (90° + α) = sec (α)
90°と異なる角度の正割:sec (90° + α) = -cosec (α)
90°と異なる角度の余接: cotan (90° + α) = -cotan (α)
180°または±π以外の角度
プラス/マイナスの角度 π (α とβ ) は、180 度異なる角度に相当します。したがって、これらは次の式を使用して表すことができます: β – α = 180° ( β 180° はαより大きくなります)。次に、これらの角度の三角比を関連付ける三角恒等式を示します。
180°とは異なる角度の正弦: sin (180° + α ) = -sin ( α )
180°とは異なる角度の余弦: cos (180° + α ) = -cos ( α )
180°とは異なる角度の正接:tan (180° + α ) = Tan ( α )
180°とは異なる角度の余割: cosec (180° + α ) = -cosec ( α )
180°と異なる角度の正割: 秒 (180° + α ) = -秒 ( α )
180°とは異なる角度の余接: cotan (180° + α ) = cotan ( α )
三角比の変換
最後に、他の演算によって特定の三角比を表現できる三角恒等式があります。したがって、比率の合計があり、それを積として表現したい場合は、これらの公式に頼ることができます。残念ながら、すべての算術演算に対応する式はありませんが、加算または減算から積へ、またはその逆のみが可能です。
加算または減算を積に変換する
次の 4 つの公式は、三角関数の加算と減算を計算するのに役立ちます。
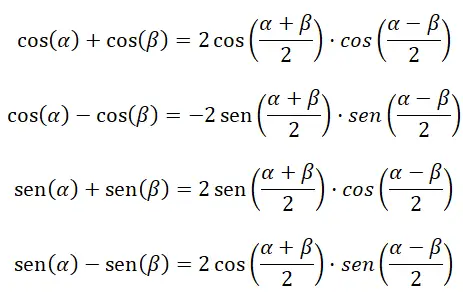
積を加算または減算に変換します
次の 4 つの公式は、三角関数の積を計算するのに役立ちます。