一次方程式または一次方程式は代数学の基礎です。これらを理解していなければ、より複雑な方程式を理解するのは非常に困難になるからです。したがって、このタイプの方程式の特徴は、単項式のリテラル部分が指数を持つことができないことです。したがって、線形方程式では、リテラル部分のない単項式と、指数のないリテラル部分を持つ単項式のみが見つかります。たとえば、 3 + x = -5 – 3xです。
また、これらの方程式には通常、一意の解がありますが、そうでない場合もあることにも注意してください。目の前にあるケースを知るには、方程式を解き、最終的に結果を分析する必要があります。したがって、2 = 0 などの不可能な等式が得られた場合、方程式には解がありません。一方、常に真となる等式が得られた場合、その解はすべての実数と等価になります。そして最後に、最後に X と数値が等しいことが得られた場合、この場合は一意の結果が得られます。
一次方程式を解く手順
方程式を解くことは、文字 (x、y、a、b…) で表される変数の値を計算することと同じです。したがって、この値を見つけるには、次の手順に従う必要があります。
- 括弧と分数を解く:まず、理解しやすい方程式を得るために、すべての括弧と分母を削除します。どの用語が未知の用語を伴うのか、どの用語が未知の用語を伴わないのかを直接認識できるため、この読み取りにより、式の解決を容易に続けることができます。
- 式を単純化しましょう。類似した用語をグループ化します (一方では独立した用語、もう一方では x を持つ用語)。したがって、一方の側では未知数の番号を残し、残りの番号を反対側に渡します。しかし、彼らの立場を変えるには、彼らのサインを変える必要があることを忘れないでください。
- 両側で演算する:すべての演算は、べき乗/根、乗算/除算、加算/減算の順序で実行します。それぞれの辺に 1 つの項が得られるまでこれを繰り返します。最終的には、4x = 8 と同じ構造を持つ方程式が得られます。
- 変数を分離します。最後に、反対側で除算して文字に付随する値を渡すだけで、最終的な値がわかります。このステップの最後には、不明な点が解決され、どのような種類の結果が残るかがわかります。一意の解、無効な解、またはすべての整数を満たした解です。
一次方程式の例
以下に、解いた一次方程式を示します。構造の複雑さに応じて、さまざまなカテゴリに分類されています。したがって、一次方程式を解くための理論的な手順と存在するさまざまなタイプを知っていれば、それらを簡単に解くために必要な知識がすでに得られているので、練習から始めます。そうは言っても、理論的な説明から始めましょう。
基本的な 1 次方程式
この最初のタイプの線形方程式は、基本的な算術演算 (加算、減算、乗算、除算) のみで構成されます。ここに 2 つの実際の例を示します。1 つ目はもう少し基本的なもので、2 つ目は計算の点でもう少し複雑です。
-6x + 4 – 1 = 6x -3
-6x + 3 = 6x – 3
-6x – 6x = -3 – 3
-12x = -6
x = 1 / 2
-24x – 3 + 4x = -4x – 27
-20x – 3 = -4x – 27
-20x + 4x = -27 + 3
-16x = -24
x = 3 / 2
括弧付きの 1 次方程式
次に、括弧内に線形方程式があります。これらは、括弧の性質を尊重する必要があるため、唯一の難点は計算にありますが、以前のものよりも解くのが少し複雑です。わかりやすくするために、実際に動作する 2 つの例を示します。
2(x + 3) – 4x = -4
2x + 6 – 4x = -4
-2x = -10
x = 5
-2 + 3 (4x + 5) = -1 (x + 2) + 2 (-3x + 2)
-2 + 12x + 15 = -x – 2 – 6x + 4
13 + 12x = -7x + 2
12x + 7x = -13 + 2
19x = -11
x = -11 / 19
累乗と根を含む 1 次方程式
3 番目のレベルは、パワーとルートを追加するだけなので、非常に単純です。これらの方程式で遭遇する可能性がある唯一の問題は、指数または根が整数の括弧に影響を与える場合 (次に示す 2 番目の例のように) ですが、それ以外はほとんど同じです。以下に 2 つの例を示します。
3² + √25 – 2x = 2³x + 4
9 + 5 – 2x = 8x + 4
14 – 2x = 8x + 4
-2x – 8x = -14 + 4
-10x = -10
x = 1
4x + (2 – 1 +5)² = 3x – √16
4x + 6² = 3x – 4
4x – 3x = -4 -36
x = -40
分数を含む 1 次方程式
私たちが見つけることができる線形方程式の最後のカテゴリはこれです。これは、以前にコメントしたすべての要素と分数で構成されます。このレベルは最も複雑で、解決するにはいくつかの方法があります。最初の最も簡単な方法は、分母に等式の反対側を掛けることです。ただし、これは分数が 2 つある場合にのみ使用できます。一方、方程式に 3 つ以上の分数がある場合は、共通の分母を見つけて、その値を同じ分数の分母で割ることによってすべての分数を乗算する必要があります。以下は各タイプの例です。
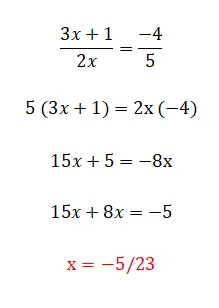
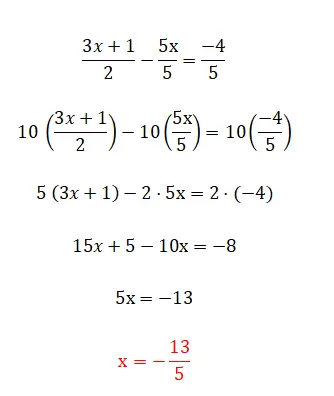
一次方程式の演習
ここで、線形方程式の演習をいくつか提供します。これらは難易度の増加に従って編成されており、最初の方程式は最後の方程式よりも簡単です。したがって、最初から始めて、どこまでできるかを確認することをお勧めします。したがって、次の方程式を解いてみて、その結果を私たちが提供する解決策と比較してください。
最初の演習
最初の演習は非常に単純な線形方程式です。これは加算と減算だけで構成されており、等式の 2 つの辺の間には 4 つの項しかありません。
2x – 3 = 4x + 5
2x – 4x = 5 + 3
-2x = 8
x = 8 / (-2)
x = -4
- 類似した用語をグループ化します。
- 両側を単純化します。
- 未知のものを消去し、その価値を計算します。
2番目の演習
この場合、括弧で形成された方程式が表示されます。最優先事項は括弧を削除して、類似した用語をグループ化できるようにすることです。
-4(x + 2) + 5x = 6 + 5x
-4x – 8 + 5x = 6 + 5x
-4x + 5x – 5x = 6 + 8
-4x = 14
x = 14 / (-4) = -7 / 2
- 括弧を解きます。
- x を左に移動し、独立項を右に移動します。
- 私たちは未知の部分を明らかにします。
結果を単純化します。
3回目の練習
次に、括弧付きの別の二次方程式を解く必要がありますが、これは少し難しくなります。これは、括弧が入れ子になっているためです (括弧が他の括弧の中にある)。したがって、最初に内部関係者、次に部外者というように、解決の順序に正しく従う必要があります。
3x + 2 (x – (4x – 5)) = 1 – (3 (2x + 7) – 2)
3x + 2 (x – 4x + 5) = 1 – (6x + 21 – 2)
3x + 2x – 8x + 10 = 1 – 6x – 21 + 2
-3x + 10 = -6x – 18
3x = -28
x = -28 / 3
- まずは内側の括弧を解くことから始めます。
- 次に、外側のかっこを解決します。
- 等式の両辺を単純化し、類似した用語を集めます。
- x を分離し、その値を計算します。
4番目の練習
この演習では、おそらく線形方程式の最も複雑な要素である分数について見ていきます。ただし、理論を読んでいれば、その方法は完全にわかっているので、心配する必要はありません。
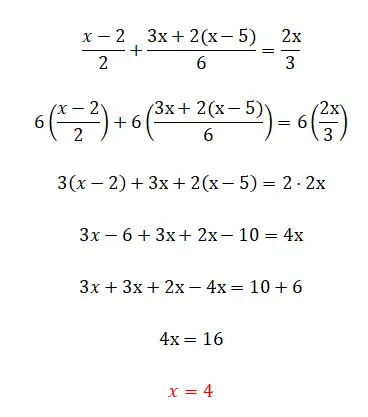
5 番目の演習
この 5 番目の演習では、括弧内に分数が表示されます。これは、解決階層が少し複雑になることを意味します。この例は、最小公倍数法を使用する方法と、分数を直接操作する方法の 2 つの方法を使用して解くことができることに注意してください。以下に 2 つの完全な手順を示します。
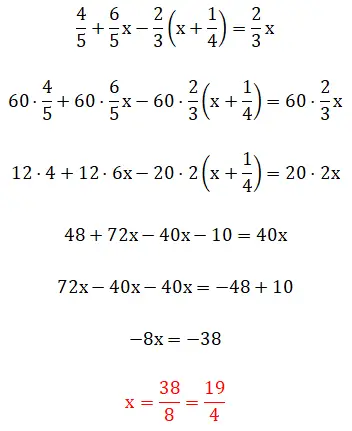
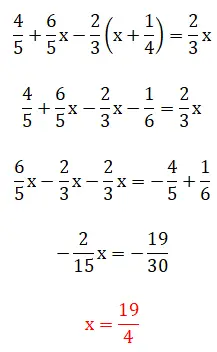
6番目の練習
次に、括弧がネストされているため、分数と括弧についてもう少し詳しく説明します。この演習では、前の演習と比べて複雑な点は多くありません。計算の点で少し難しいだけです。それだけです。
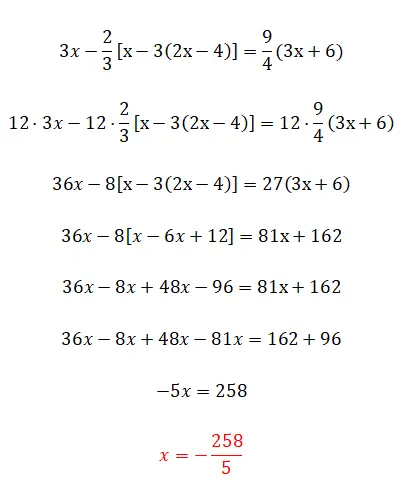
- すべての項に分母の lcmp を掛けます。
- 括弧を削除して式を簡略化します。最初に内側の括弧、次に外側の括弧を削除します。
- それぞれの側で類似した用語をグループ化します。
- それぞれの側で操作を解決します。
- そして未知の値を計算します。
7回目の練習
次の演習は非常に簡単に思えるかもしれませんが、少し変わった結果が得られるはずなので、とにかく解いてみることをお勧めします。試した後は、演習の下にある解決策と説明を見てください。
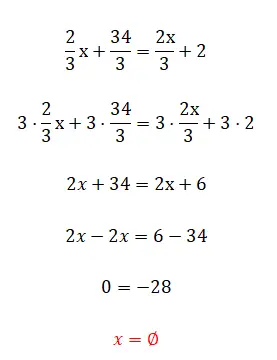
- すべての分数に分母の lcm を掛けます。
- 得られた式を簡略化していきます。
- そして最後に、未知のものを排除したため、それが誤った平等をもたらすことがわかります。
お気づきかと思いますが、方程式を正しく完成させる値が存在しないため、これは偽の等式、または結果のない等式です。これは、冒頭で述べたケースの 1 つです。
8回目の練習
最後に、この演習を紹介します。この演習には、この記事全体で見た複雑な要素がすべて含まれているため、非常に複雑ですが、少しコツもあります。この 1 次方程式を解くことができれば、理論全体を完全に理解したことになるとコメントしてください。そうでない場合でも、この演習は非常に複雑であるため、心配する必要はありません。
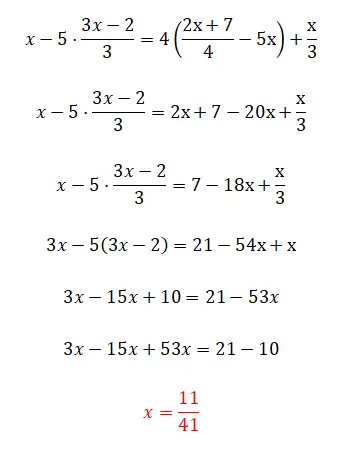
- まず、方程式の右側の 4 つを削除します。
- 次に、右側の x を結合します。
- 分母を取り除くために、すべての項に 3 を掛けます。
- 括弧を削除します。
- 似たような用語をまとめてみました。
- 未知の値を計算します。
さらに線形方程式の演習を行う
十分な練習を積んだので、複雑な一次方程式を解けるようになるはずです。ただし、引き続き練習したい場合は、このワークシートを解いてみることをお勧めします。ただし、十分に説明したと思われる場合は、操作の階層を理解するのに役立つ記事も提供します。こうすることで、どの計算を最初に解けばよいのかが常にわかり、間違いを犯すことがなくなります。