ルッフィーニの法則は、 パオロ ルッフィーニによって開発された数学的手続きであり、(x – a) の形式の多項式を除算することができます。この数学的手法は合成除算とも呼ばれます。しかし、この手順はどのように使用され、どのような手順で行われるのでしょうか?では、電卓を使ってルフィニの練習問題を解くにはどうすればよいでしょうか?この記事ではこれらすべてをまとめてわかりやすく説明し、さらに、Ruffini に最適な電卓をお勧めします。
オンラインのルフィニ電卓
多項式を因数分解する場合は、この計算機を使用できます。これを使用すると、 ^ (累乗) と / (除算) の記号を使用して式を記述する限り、任意の式を因数分解できます。この計算機は 3 次以上の多項式を因数分解できるので、安心してください。したがって、これはオンラインで多項式を因数分解するための究極の計算ツールです。
ルッフィーニの塗り方は?
このセクションでは、ルッフィーニの実行方法を説明し、そのメソッドを使用して具体的な例を解きます。これにより、手順全体を明確かつグラフィカルに確認できるようになります。そうすることで、この概念を根幹から理解することができ、試験の後半でそれを思い出すことができます。また、文章の説明では疑問があった方でも理解できるよう、解説動画も掲載しています。
Ruffini メソッドを使用するための要件
多項式の割り算を解く前、または多項式を因数分解する前に、約数を確認する必要があります。第一学位であれば、ルッフィーニ法で進めることができます。一方、約数の次数が 1 より大きい場合、この手順に従って計算を解くことはできません。したがって、多項式を分割するには他の方法を使用する必要があります。これは、計算を開始する前に確認する必要がある要素です。そうしないと、多くの時間が無駄になる可能性があります。
ルッフィーニの法則を使用して多項式を分割する手順
この数学的リソースがいつ使用できるかがわかったので、多項式を因数分解できるようにするために従うべきさまざまな手順を見ていきます。したがって、(x3+3x²-1) / (x-2) の例から、まず被除数係数を水平線に書き、欠落している項をゼロで表す必要があります。次に、画像に示すように、約数の独立項を別の反対符号に置きます。
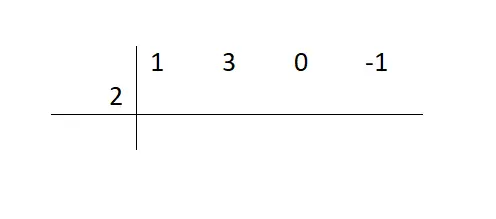
次に、最初の係数 (より高い指数に上げられた変数に付随する係数) を下げる必要があります。この数値を減らして次のステップに進むため、この数値については何もしません。
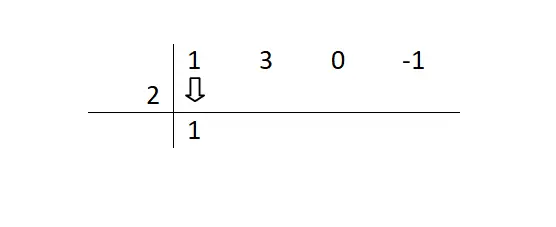
次に、かなり反復的な一連の手順を開始します。減った数値に除数を掛け、その結果を次の項に置きます。次に、この結果の間に次の項を追加し、最初に書き留めた数値の隣に書きます。
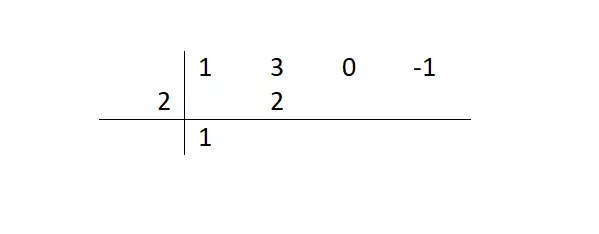
テーブルが完成するまでこの一連の手順に従うと、次のレイアウトが得られます。このようにして、剰余が 19 (最後に計算した数値) に等しいことがわかり、剰余の式 (商) が x²+5x+10 になることがわかります。これらの情報はすべて、下の行の数字から得られました。また、多項式を因数分解する場合は、この商を使用して他の根を求め続ける必要があります。
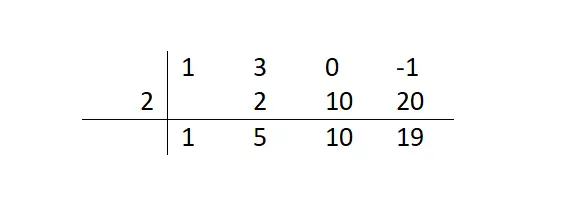
ルッフィーニを電卓に入力するにはどうすればよいですか?
電卓上で Ruffini を使用して多項式を除算できるようにするには、電卓のソルバーにアクセスするだけです。つまり、方程式計算モードにアクセスするだけです。そして、内部に入ったら、多項式を因数分解したいので、多項式方程式オプションを選択します。次に、式の次数を選択し、数学エディタに入ることができるので、式を導入します。したがって、多項式の根を取得するときは、それを (x – a) の形式で記述するだけで済みます。この手順全体 (ルート部分を除く) は、電卓を使用して方程式を解くために使用する手順と同じです。
ルッフィーニの定理を計算するための最高の電卓
現在、多項式を使った演算を解いたり、因数分解したりできる計算機が数多く見つかります。しかし、使いやすさと価格の点で際立ったモデルがいくつかあります。 2 つの良い例は、 Casio FX-991SPX IIとCasio FX-991ES PLUSです。実際、前のセクションで行った説明は、これら 2 つのモデルの動作に基づいています。ただし、すでに述べたように、Ruffini を完璧に実行するのに役立つ関数電卓は他にもあります。
ルッフィーニの例と演習
ルッフィーニの規則は、最初に説明した規則に従っている限り、2 つの多項式をランダムに取ることによって実践できます。ただし、この数学的手順を通じて 1 より大きい次数の多項式を因数分解してみることもできます。したがって、同じ数学的メカニズムを確認し、次に多項式の根の概念を確認します。次に、因数分解する必要がある 2 つの多項式と、ルフィニの方法を使用して解く必要がある非常に単純な除算を示します。
演習 1
多項式を因数分解します: 2x³-7x²+8x-3
ルート: x=1 および x=1、したがって (x-1)²(2x-3) が残ります。
演習 2
多項式を因数分解します: x³+2x²-x-2
ルート: x=-2、x=-1、x=1 なので、(x+2)(x+1)(x-1) が残ります。
演習 3
次の多項式間の除算を解きます: (3×3-5×2+2) / (x-2)
商: 3x²+x+2、余り: 6
Ruffini の演習をさらに詳しく知りたい場合は、この記事と同じ手順を説明しているSuperprof の記事を参照することをお勧めします。ただし、Ruffini とは少し異なる例と演習があるため、さらに練習することでいくつかの疑問を解決できるかもしれません。いずれにせよ、私たちのコンテンツと Ruffini Calculator がお役に立てば幸いです。