このページでは、単項式を使用したすべての演算 (加算、減算、乗算、除算、べき乗) を実行する方法を説明します。さらに、単項式を使用した各タイプの演算の例を確認し、段階的に解決される演習で練習することができます。
単項式の加算と減算
2 つ以上の単項式は、それらが類似した単項式である場合、つまり 2 つの単項式が同一のリテラル部分 (同じ文字と同じ指数) を持つ場合にのみ加算または減算できます。
次に、2 つの類似した単項式の和 (または減算) は、同じリテラル部分で構成される別の単項式と、これら 2 つの単項式の係数の和 (または減算) に等しくなります。


単項式の加算および減算は、それぞれ単項式の加算および減算とも呼ばれます。
単項式の加算と減算の例
2 つ以上の単項式を加算および減算する方法を明確に理解できるように、以下にいくつかの例を示します。
最後の例の単項式は、類似していない、つまり未知数または指数が異なるため、加算または減算できません。
単項式の積
単項式と数値の積を解くには、単項式のリテラル部分をそのままにして、単純に単項式の係数にその数値を乗算します。
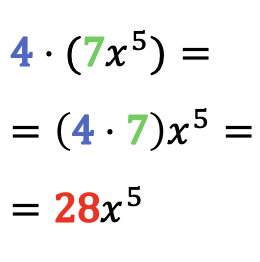
数値と単項式の乗算の例
単項式の乗算
2 つの単項式の乗算の結果は別の単項式であり、その係数は単項式の係数の積であり、そのリテラル部分は同じ基数を持つ変数を乗算することによって、つまりそれらの指数を加算することによって取得されます。

したがって、2 つの異なる単項式を乗算するには、それらの間の係数を乗算し、同じ底を持つべき乗の指数を加算する必要があります。
ただし、異なる基本べき乗を持つ 2 つの単項式を乗算する場合は、それらの係数を単純に乗算し、べき乗を同じにする必要があります。例えば:
![]()
一方、単項式を乗算する場合は、符号の法則を考慮する必要があります。
- 正の単項式に正の単項式を掛けると、別の正の単項式が得られます。
- 正の単項式と負の単項式を乗算すると (またはその逆)、負の単項式と等しくなります。
- 2 つの負の単項式を乗算すると、正の単項式が生成されます。
単項乗算の例
以下は単項式間の乗算の例をいくつか示しており、どのように行われるかを確認できます。
これまで見てきたように、単項式の乗算を解くのは比較的簡単です。ただし、単項式は多項式で乗算することもでき、2 つ以上の多項式を一緒に乗算することもできることに留意する必要があります。さらに興味がある場合は、 「多項式乗算」をクリックすると、これらすべての演算がどのように機能するかを確認できます。
単項式の除算
数学では、単項式の除算の結果は別の単項式であり、その係数は単項式の係数の商に等しく、そのリテラル部分は同じ底を持つ変数を除算すること、つまり指数を減算することによって得られます。 。

明らかに、単項式の割り算は分数として表すこともできます。
![]()
掛け算と同様に、単項式の割り算にも符号の法則を適用する必要があります。
- 正の単項式を正の単項式で割ると、別の正の単項式が得られます。
- 正の単項式を負の単項式で割ったもの (またはその逆) は、負の単項式と同等です。
- 2 つの負の単項式を互いに割ると、正の単項式が生じます。
単項式の割り算の例
2 つ以上の単項式がどのように分割されるかの他の例を以下に示します。
確かに、ある時点で、数学で何か新しいことを学んだとき、あなたは自問しました。「それは何のためにあるのですか?」さて、単項式除算は多項式を除算するために使用されます。実際、2 つの単項式が間違って除算されたために、多項式の除算を間違えるのはよくあることです。そのため、単項式間の除算に慣れてきたら、 多項式の除算がどのように計算されるかを確認することをお勧めします。手順を学ぶのがはるかに簡単になるからです (これは非常に複雑です)。
単項式のべき乗
数学では、単項式の累乗を計算するには、単項式の各要素を累乗します。言い換えれば、単項式のべき乗は、その係数とその変数 (文字) をべき乗することで構成されます。

べき乗の性質から、両方がすでに高い項を引き上げると、指数が倍増することを思い出してください。これが、単項式の累乗において、各文字の指数に常に累乗を示す指数が乗算される理由です。
一方、この操作を正しく実行するには、次のべき乗の性質を覚えておく必要があります。
- 負の単項式を偶数乗したものは、正の単項式と同等です。
- 代わりに、負の単項式を奇数乗すると負の単項式になります。
単項式の累乗の例
単項式の累乗がどのように計算されるかを明確に理解できるように、いくつかの例を示します。
単項式と組み合わせた演算
単項式を使用したすべての演算が何であるかを理解したら、それらを相互に組み合わせることもできることを理解してください。つまり、加算、減算、乗算、除算、累乗など、すべての型が関係する単項式の演算を解くように求められる演習が見つかります。
しかし、心配しないでください。見た目ほど難しいものではありません。覚えておく必要があるのは、結合された操作が解決される順序だけです。
- まず、括弧内の単項式を含む演算を解きます。
- 次に、単項式のべき乗が計算されます。
- 第三に、単項式の乗算と除算が実行されます。
- そして最後に、単項式の加算と減算が決定されます。
例を解いてみると、より明確に理解できると思います。
単項式の組み合わせ演算の例
![]()
まず第一に、括弧内の単項式を使用して演算を解く必要があります。
![]()
この場合、私たちには力がありません。それでは、単項式の乗算と除算を計算してみましょう。
![]()
最後に、単項式を加算および減算します。
![]()
![]()
単項式を使用した演算に関する演習を解決しました
練習したい場合に備えて、単項式を使用した演算に関する ESO の難易度を段階的に解決するいくつかの演習を以下に残しておきます。
演習 1
次の単項式の加算と減算を計算します。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
演習 2
次の単項式の乗算を解きます。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![\text{F)} \ 7x^3y^2 \cdot 5x^8z^4 \cdot (-2x^2y^5z^3)= <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-bb20ebb96e0dff759d07813f6fff9470_l3.png" height="22" width="195" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[35x^{11}y^2z^4\cdot (-2x^2y^5z^3) =\]" title="Rendered by QuickLaTeX.com"/> \bm{-70x^{13}y^7z^7}” title=”Rendered by QuickLaTeX.com”></p>
</p>
<div class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-d92004db2f9cc2fc28f7b5358dcb5932_l3.png)
![\text{F)} \ 48x^8y^6z^{10} : (-6x^4y^{2}z^4) : (-4x^2y^2z^3)=<span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-6dc0e068dbf84cef6abfe7e1789d245b_l3.png" height="22" width="194" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[-8x^4y^4z^6: (-4x^2y^2z^3)=\]" title="Rendered by QuickLaTeX.com"/> \bm{2x^2y^2z^3}” title=”Rendered by QuickLaTeX.com”></p>
</p>
<div class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-1b1554d59ad6a39e24db564712789ee7_l3.png)