ベクトルの線形結合 -

このページでは、ベクトル間の線形結合が何を意味するのかについて説明します。また、ベクトルが一次結合として表現される例を見ることができ、さらに、段階的に解く演習や問題で演習することができます。

ベクトルの線形結合とは何ですか?

線形結合の定義は次のとおりです。

ベクトルのセットの線形結合は、セット内のすべてのベクトルを加算してスカラー (実数) を乗算して得られるベクトルです。

言い換えれば、ベクトルのセットが与えられると、

$\vv{\text{v}}_1, \vv{\text{v}}_2,\ldots \vv{\text{v}}_n,$

それらの線形結合は次のようになります。

$\vv{\text{w}}=a_1\vv{\text{v}}_1+a_2\vv{\text{v}}_2+\dots + a_n\vv{\text{v}}_n$

ここで係数は

$a_i$

これらは実数です。

したがって、他のベクトルの線形結合であるベクトルは、最初のベクトルを 2 番目のベクトルで表現できることを意味します。

この概念は、2 つのベクトルの線形結合であるベクトルを平面にグラフ化することでよりよく理解できます。

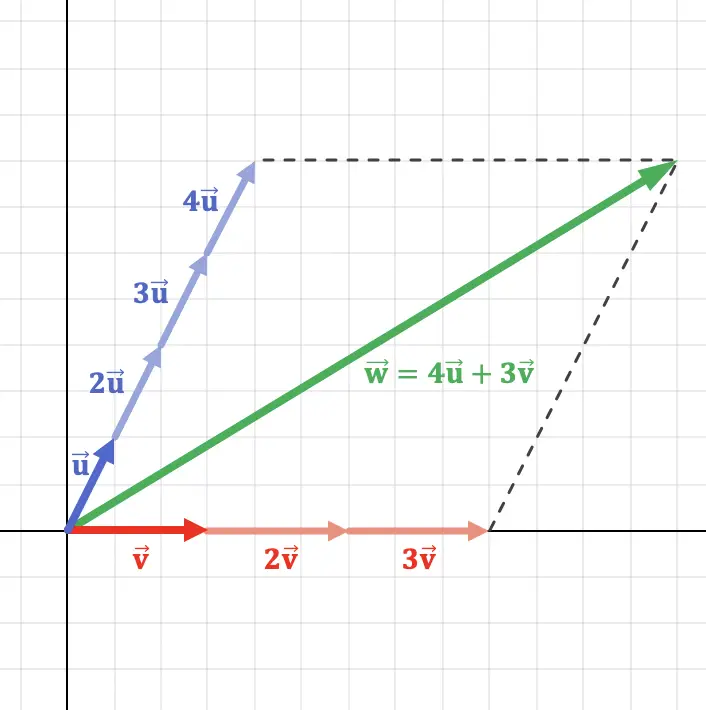
上のグラフでわかるように、ベクトルは

$\vv{\text{w}}$

ベクトルから取得できます

$\vv{\text{u}}$

そして

$\vv{\text{v}}$

ベクトル演算を実行します。したがって、ベクトルは

$\vv{\text{w}}$

は、他の 2 つのベクトルの線形結合です。

この線形結合は一意であること、つまり、各ベクトルに対して実行可能な線形結合は 1 つだけであることを強調しておく必要があります。前の例に従って、乗算すると、

$\vv{\text{u}}$

4 ではなく 6 の場合、別の異なるベクトルが得られます。

さらに、平面 (R2) での線形結合の特性の 1 つは、方向が異なる場合、つまり平行でない場合、任意のベクトルを他の 2 つのベクトルの線形結合として置くことができることです。

また、2 つのベクトルが線形結合であることを目で確認できる場合もあります。これを行うには、コンポーネントが比例するだけで十分です。たとえば、次の 2 つのベクトルの座標は比例するため、これらのベクトルは線形結合になります。

$\vv{\text{u}} = (1,2,-1) \qquad \vv{\text{v}} = (3,6,-3)$

$\cfrac{3}{1} = \cfrac{6}{2} = \cfrac{-3}{-1} = 3 \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \begin{array}{c} \text{Combinaci\'on}\\[2ex] \text{lineal} \end{array}$

最後に、2 次元 (R2 内) ベクトル空間でも 3 次元 (R3 内) ベクトル空間でも、ベクトルのセット内に線形結合がある場合、これはそれらが互いに線形依存していることを意味します。一方、ベクトル間で線形結合が不可能な場合、これはそれらが線形独立であることを意味します。

この最後の概念が完全に理解できない場合は、線形依存ベクトルと独立ベクトルの説明を確認することをお勧めします。ここでは、ベクトルが線形依存または独立であることの意味、各タイプの例とそれらの違いについて説明します。。この概念はよく使われており、実際試験でもよく問われるため、よく理解することが重要です。

ベクトルを他のベクトルの線形結合として表現する方法

次に、ベクトルの線形結合を求める典型的な問題を解決する方法を見ていきます。

ベクトルを表現する
$\vv{\text{x}}$

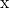
の線形結合として

$\vv{\text{u}}, \vv{\text{v}}$

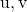
そして

$\vv{\text{w}}.$

$\vv{\text{x}} = (3,1,2)$

$\vv{\text{u}} = (1,0,1) \qquad \vv{\text{v}} = (1,2,0) \qquad \vv{\text{w}} = (0,1,-1)$

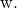
したがって、ベクトルは

$\vv{\text{x}}$

が他のベクトルの線形結合である場合、次の方程式を満たす必要があります。

$a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}=\vv{\text{x}}$

ここで係数は

$a_1, a_2$

そして

$a_3$

これらは私たちが見つけなければならない未知のものです。

したがって、各ベクトルをその座標で置き換えます。

$a_1\begin{pmatrix} 1 \\0\\1 \end{pmatrix}+a_2\begin{pmatrix} 1 \\2\\0 \end{pmatrix}+ a_3\begin{pmatrix} 0 \\1\\-1 \end{pmatrix}=\begin{pmatrix} 3 \\1\\2 \end{pmatrix}$

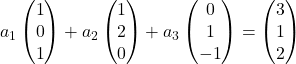
各ベクトルにその係数を乗算します。

$\begin{pmatrix} a_1 \\0\\a_1 \end{pmatrix}+\begin{pmatrix} a_2 \\2a_2\\0 \end{pmatrix}+ \begin{pmatrix} 0 \\a_3\\-a_3 \end{pmatrix}=\begin{pmatrix} 3 \\1\\2 \end{pmatrix}$

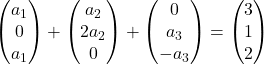
ベクトルを追加します。

$\begin{pmatrix} a_1 +a_2\\2a_2+a_3\\a_1-a_3 \end{pmatrix}=\begin{pmatrix} 3 \\1\\2 \end{pmatrix}$

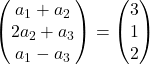
各左座標は各右座標と等しくなければなりません。したがって、次の 3 つの方程式が得られます。

$\left. \begin{array}{l} a_1 +a_2 = 3 \\[2ex] 2a_2+a_3 =1\\[2ex] a_1-a_3 = 2 \end{array} \right\}$

残っているのは、得られた連立方程式を解くことだけです。これを行うには、好みの方法 (置換法、クラマーの法則、ガウスジョーダン法など) を使用します。この場合はガウス法を使用します。

$\left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 1&0&-1&2 \end{array} \right)$

$\left(\begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 1&0&-1&2 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{F_3-F_1} \end{array} \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&-1&-1&-1 \end{array} \right)$

$\left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&-1&-1&-1 \end{array} \right)\begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{2F_3+F_2}\end{array} \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&0&-1&-1 \end{array}\right)$

したがって、得られるステップ系は次のようになります。

$\left. \begin{array}{r} a_1 +a_2 = 3 \\[2ex] 2a_2+a_3 =1\\[2ex] -a_3 = -1 \end{array} \right\}$

私たちが今しなければならないのは、未知の部分を明らかにし、その価値を見つけることだけです。したがって、最後の方程式から次のようになります。

$a_3:$

$-a_3 = -1 \ \longrightarrow \ \bm{a_3 = 1}$

システムの 2 番目の方程式から、次の値を計算します。

$a_2:$

$2a_2+a_3 =1 \ \xrightarrow{a_3\ = \ 1} \ 2a_2+1=1$

$2a_2=1-1$

$2a_2=0$

$\bm{a_2=0}$

そして最後に、ステップ系の最初の方程式から未知のものを見つけます。

$a_1:$

$a_1 +a_2 = 3 \ \xrightarrow{a_3\ = \ 1 \ ; \ a_2 \ = \ 0 } \ \bm{a_1 = 3}$

したがって、線形方程式系の解は次のようになります。

$a_1=3 \qquad a_2=0 \qquad a_3 = 1$

したがって、ベクトルは

$\vv{\text{x}}$

これは次の線形結合で表すことができます。

$\vv{\text{x}}= a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}$

$\vv{\text{x}}= 3\vv{\text{u}}+0\vv{\text{v}}+ 1\vv{\text{w}}$

$\vv{\mathbf{x}}\bm{= 3}\vv{\mathbf{u}} \bm{+} \vv{\mathbf{w}}}$

したがって、ベクトル間には事実上線形依存関係が存在します。一方、連立方程式の解が得られなかった場合、これはベクトルが

$\vv{\text{x}}$

これは他のベクトルに関して線形独立であるため、他のベクトルから前記ベクトルを取得するための可能な線形結合はありません。

ベクトルの線形結合に関する演習を解決しました。

演習 1

次の 3 つのベクトルのうち、どのペアが互いに線形結合であるかを示します。さらに、前記ベクトルのペアの線形結合関係を見つけます。

$\vv{\text{u}} = (2,4,3) \qquad \vv{\text{v}} = (1,2,-3) \qquad \vv{\text{w}} = (-3,-6,9)$

解決策を見る

ベクトルのペアが線形結合であるかどうかを知るには、それらの座標が比例しているかどうかを確認する必要があります。

まずベクトルを確認します

$\vv{\text{u}}$

ベクトルを使って

$\vv{\text{v}} :$

$\cfrac{2}{1} = \cfrac{4}{2} \neq \cfrac{3}{-3} \ \longrightarrow \ \text{No proporcionales}$

次に、ベクトルを確認します。

$\vv{\text{u}}$

ベクトルを使って

$\vv{\text{w}} :$

$\cfrac{2}{-3} = \cfrac{4}{-6} \neq \cfrac{3}{9} \ \longrightarrow \ \text{No proporcionales}$

最後に、ベクトルをテストします。

$\vv{\text{v}}$

ベクトルを使って

$\vv{\text{w}} :$

$\cfrac{1}{-3} = \cfrac{2}{-6} = \cfrac{-3}{9} = -\cfrac{1}{3} \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \begin{array}{c} \text{Combinaci\'on}\\[2ex] \text{lineal} \end{array}$

したがって、線形結合であるベクトルの唯一のペアは次のとおりです。

$\vv{\text{v}}$

そして

$\vv{\text{w}}.$

さらに、それらの関係は次のとおりです。

$\vv{\text{v}}= -\cfrac{1}{3} \vv{\text{w}}$

または同等のもの:

$\vv{\text{w}}= -3 \vv{\text{v}}$

このステートメントでは必須ではありませんが、相互に線形に依存するベクトルは次のとおりです。

$\vv{\text{v}}$

そして

$\vv{\text{w}}$

なぜならそれらの間には線形結合があるからです。他のペアは線形的に結合できないため、線形的に独立しています。

演習 2

ベクトル間の線形関係を見つけます。

$\vv{\text{x}}$

そしてベクトルのセット

$\vv{\text{u}}, \vv{\text{v}}$

そして

$\vv{\text{w}}.$

$\vv{\text{x}} = (4,2,5)$

$\vv{\text{u}} = (1,-1,0) \qquad \vv{\text{v}} = (1,2,2) \qquad \vv{\text{w}} = (-1,1,-1)$

解決策を見る

したがって、ベクトルは

$\vv{\text{x}}$

が他のベクトルの線形結合である場合、次の方程式を満たす必要があります。

$a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}=\vv{\text{x}}$

したがって、各ベクトルをその座標で置き換えます。

$a_1\begin{pmatrix} 1 \\-1\\0 \end{pmatrix}+a_2\begin{pmatrix} 1 \\2\\2 \end{pmatrix}+ a_3\begin{pmatrix} -1 \\1\\-1 \end{pmatrix}=\begin{pmatrix} 4 \\2\\5 \end{pmatrix}$

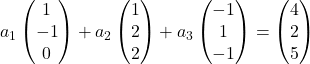
各ベクトルにその定数を乗算します。

$\begin{pmatrix} a_1 \\-a_1\\0 \end{pmatrix}+\begin{pmatrix} a_2 \\2a_2\\2a_2 \end{pmatrix}+ \begin{pmatrix} -a_3 \\a_3\\-a_3 \end{pmatrix}=\begin{pmatrix} 4 \\2\\5 \end{pmatrix}$

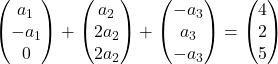
ベクトルを追加します。

$\begin{pmatrix} a_1 +a_2-a_3\\-a_1+2a_2+a_3\\ 2a_2-a_3 \end{pmatrix}=\begin{pmatrix} 4 \\2\\5 \end{pmatrix}$

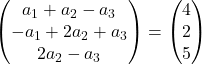
したがって、次の連立方程式が得られます。

$\left. \begin{array}{l} a_1 +a_2-a_3 = 4 \\[2ex] -a_1+2a_2+a_3 =2\\[2ex] 2a_2-a_3 = 5 \end{array} \right\}$

ガウス法で得られた系を解きます。

$\left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] -1&2&1&2\\[2ex] 0&2&-1&5 \end{array} \right)$

$\left(\begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] -1&2&1&2\\[2ex] 0&2&-1&5 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{F_2+F_1}\\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&2&-1&5\end{array} \right)$

$\left(\begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&2&-1&5 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{3F_3-2F_2} \end{array} \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&0&-3&3\end{array} \right)$

したがって、得られるステップ系は次のようになります。

$\left. \begin{array}{r} a_1 +a_2-a_3 = 4 \\[2ex] 3a_2 =6\\[2ex] -3a_3 = 3 \end{array} \right\}$

$a_3:$

$-3a_3 = 3$

$a_3 = \cfrac{3}{-3} = -1$

システムの 2 番目の方程式から、次の値を計算します。

$a_2:$

$3a_2=6$

$a_2=\cfrac{6}{3} = 2$

そして最後に、ステップ系の最初の方程式から未知のものを見つけます。

$a_1:$

$a_1 +a_2-a_3 = 4 \ \xrightarrow{a_3\ = \ -1 \ ; \ a_2 \ = \ 2 } \ a_1 +2-(-1) = 4$

$a_1 = 4-2-1$

$a_1 = 1$

したがって、線形方程式系の解は次のようになります。

$a_1=1 \qquad a_2=2 \qquad a_3 = -1$

したがって、ベクトルは

$\vv{\text{x}}$

これは次の線形結合で表すことができます。

$\vv{\text{x}}= a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}$

$\vv{\text{x}}= 1\vv{\text{u}}+2\vv{\text{v}}-1\vv{\text{w}}$

$\vv{\mathbf{x}}\bm{= }\vv{\mathbf{u}}\bm{+} \bm{2} \vv{\mathbf{v}} \bm{-} \vv{\mathbf{w}}$

演習 3

ベクトルを表現する

$\vv{\text{x}}$

ベクトルの線形結合として

$\vv{\text{u}}, \vv{\text{v}}$

そして

$\vv{\text{w}}.$

$\vv{\text{x}} = (-1,5,-3)$

$\vv{\text{u}} = (1,3,-1) \qquad \vv{\text{v}} = (2,-3,-2) \qquad \vv{\text{w}} = (0,-2,1)$

解決策を見る

ベクトルに関する線形結合方程式を提案します。

$\vv{\text{x}} :$

$a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}=\vv{\text{x}}$

したがって、各ベクトルをそのコンポーネントで置き換えます。

$a_1\begin{pmatrix} 1 \\3\\-1 \end{pmatrix}+a_2\begin{pmatrix} 2 \\-3\\-2 \end{pmatrix}+ a_3\begin{pmatrix} 0 \\-2\\1 \end{pmatrix}=\begin{pmatrix} -1 \\5\\-3 \end{pmatrix}$

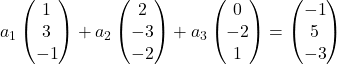
各ベクトルにそれぞれの未知数を乗算します。

$\begin{pmatrix} a_1 \\3a_1\\-a_1 \end{pmatrix}+\begin{pmatrix} 2a_2 \\ -3a_2\\ -2a_2 \end{pmatrix}+ \begin{pmatrix} 0 \\-2a_3\\a_3 \end{pmatrix}=\begin{pmatrix} -1 \\5\\-3 \end{pmatrix}$

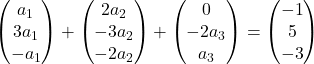
ベクトルの加算を実行します。

$\begin{pmatrix} a_1 +2a_2\\3a_1-3a_2-2a_3\\ -a_1-2a_2+a_3 \end{pmatrix}=\begin{pmatrix} -1 \\5\\-3 \end{pmatrix}$

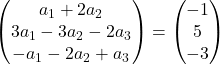
したがって、次のような連立方程式が得られました。

$\left. \begin{array}{l} a_1 +2a_2 = -1 \\[2ex] 3a_1-3a_2-2a_3 =5\\[2ex] -a_1-2a_2+a_3 = -3 \end{array} \right\}$

ガウス法で得られた系を解きます。

$\left( \begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 3&-3&-2&5\\[2ex] -1&-2&1&-3 \end{array} \right)$

$\left(\begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 3&-3&-2&5\\[2ex] -1&-2&1&-3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{F_2-3F_1}\\[2ex] \xrightarrow{F_3+F_1} \end{array} \left( \begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 0&-9&-2&8\\[2ex] 0&0&1&-4\end{array} \right)$

したがって、得られるステップ系は次のようになります。

$\left. \begin{array}{r} a_1 +2a_2 = -1 \\[2ex] -9a_2-2a_3 =8\\[2ex] a_3 = -4 \end{array} \right\}$

$a_3:$

$a_3 = -4$

システムの 2 番目の方程式から、次の値が求められます。

$a_2:$

$-9a_2-2a_3 =8 \ \xrightarrow{a_3 \ = \ -4} \ -9a_2-2\cdot (-4) = 8$

$-9a_2+8 = 8$

$-9a_2 = 8-8$

$-9a_2 = 0$

$a_2=\cfrac{0}{-9} = 0$

そして最後に、ステップ系の最初の方程式から未知の問題を解きます。

$a_1:$

$a_1 +2a_2 = -1 \ \xrightarrow{a_2 \ = \ 0 } \ a_1=-1$

したがって、線形方程式系の解は次のようになります。

$a_1=-1 \qquad a_2=0 \qquad a_3 = -4$

したがって、ベクトルは

$\vv{\text{x}}$

は他のベクトルを線形結合することで表現できます。

$\vv{\text{x}}= a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}$

$\vv{\text{x}}= -1\vv{\text{u}}+0\vv{\text{v}}-4\vv{\text{w}}$

$\vv{\mathbf{x}}\bm{= -}\vv{\mathbf{u}}\bm{-4} \vv{\mathbf{w}}$

演習 4

ベクトルかどうかを判断します。

$\vv{\text{x}}$

ベクトルからの線形結合として表現できます

$\vv{\text{u}}, \vv{\text{v}}$

そして

$\vv{\text{w}}.$

この場合、それらを接続する表現を見つけてください。

$\vv{\text{x}} = (2,1,-1)$

$\vv{\text{u}} = (3,-1,1) \qquad \vv{\text{v}} = (-1,2,0) \qquad \vv{\text{w}} = (1,3,1)$

解決策を見る

したがって、ベクトルは

$\vv{\text{x}}$

が他のベクトルの線形結合である場合、次の方程式を満たす必要があります。

$a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}=\vv{\text{x}}$

したがって、各ベクトルをその座標で置き換えます。

$a_1\begin{pmatrix} 3 \\-1\\1 \end{pmatrix}+a_2\begin{pmatrix} -1 \\2\\0 \end{pmatrix}+ a_3\begin{pmatrix} 1 \\3\\1 \end{pmatrix}=\begin{pmatrix} 2 \\1\\-1 \end{pmatrix}$

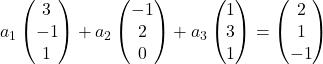
各ベクトルにその係数を乗算します。

$\begin{pmatrix} 3a_1 \\-a_1\\a_1 \end{pmatrix}+\begin{pmatrix} -a_2 \\2a_2\\0 \end{pmatrix}+ \begin{pmatrix} a_3 \\3a_3\\a_3 \end{pmatrix}=\begin{pmatrix} 2 \\1\\-1 \end{pmatrix}$

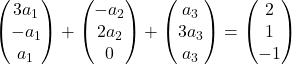
ベクトルを追加します。

$\begin{pmatrix} 3a_1 -a_2+a_3\\-a_1+2a_2+3a_3\\ a_1+a_3 \end{pmatrix}=\begin{pmatrix} 2 \\1\\-1 \end{pmatrix}$

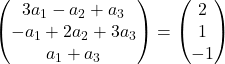
したがって、前の式は次の連立方程式と等価です。

$\left. \begin{array}{l} 3a_1 -a_2+a_3 = 2 \\[2ex] -a_1+2a_2+3a_3 =1\\[2ex] a_1+a_3 = -1 \end{array} \right\}$

ここで、ガウス法によって得られたシステムを解きます。

$\left( \begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] -1&2&3&1\\[2ex] 1&0&1&-1 \end{array} \right)$

$\left(\begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] -1&2&3&1\\[2ex] 1&0&1&-1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{3F_2+F_1}\\[2ex] \xrightarrow{3F_3-F_1} \end{array} \left( \begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&1&2&-5\end{array} \right)$

$\left(\begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&1&2&-5 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5F_3-F_2} \end{array} \left( \begin{array}{ccc|c}3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&0&0&-30\end{array} \right)$

したがって、次のような連立方程式が得られました。

$\left. \begin{array}{r} 3a_1 -a_2+a_3 = 2 \\[2ex] 5a_2 +10a_3=5\\[2ex] 0 = -30 \end{array} \right\}$

ただし、未知数がどのような値を取っても 0 が -30 に等しくなることはないため、最後の方程式は決して満たされません。したがって、システムには解がなく、ベクトルを計算するための線形結合がないことを意味します。

$\vv{\text{x}}.$

ベクトルの線形結合とは何ですか?

ベクトルを他のベクトルの線形結合として表現する方法

ベクトルの線形結合に関する演習を解決しました。

演習 1

演習 2

演習 3

演習 4

コメントする 返信をキャンセル

コメントする返信をキャンセル