このページでは、ヌル行列とも呼ばれるゼロ行列について説明します。また、その要素の値が行列の次元に依存しないことも例で確認し、最後にこのタイプの行列のすべてのプロパティを見つけます。
ヌル行列とは何ですか?
ヌル行列(またはヌル行列) は、要素がすべてゼロ (0) に等しい行列です。
したがって、ゼロ行列の定義により、この行列は、その数値がすべてゼロである限り、すべての可能な次元を持つことができます。次の例を見てください。
ヌル行列の例
2 × 2 ヌル行列の例
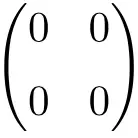
3 × 3 ヌル行列の例
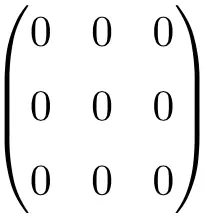
4 × 4 ヌル行列の例
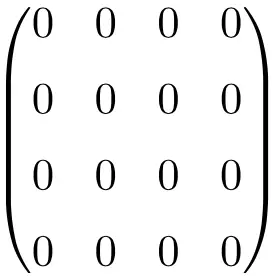
この特定の行列は単にゼロでいっぱいの行列であるため、重要ではないように思われるかもしれません。ただし、数学、特に線形代数の分野では、計算がはるかに簡単になるため、非常に便利な行列です。
ヌル行列のプロパティ
Null (または Null) 行列には次の特性があります。
- ゼロ行列は行列加算演算の中立要素であるため、次のようになります。
![]()
- 行列の乗算にはゼロの乗算特性があります。つまり、任意の行列にゼロ行列を乗算した積は 0 に等しくなります。
![]()
- 行列が正方行列の場合、ゼロ行列は対称と非対称の両方になります。
- ゼロ行列は、ランクがゼロである唯一の行列です。
- ゼロ行列の行列式は常に 0 と評価されるため、このタイプの行列には逆行列がありません (特異行列です)。
- 明らかに、ゼロ行列は零ポテント行列の一例です。