ニュートンの二項式は、 2 つの項の和を所定の累乗で表すために使用される数式です。この公式は英国の数学者アイザック ニュートンにちなんで名付けられ、数学の多くの分野で使用されています。
たとえば、統計、確率論、微分積分に役立ちます。二項定理を使用すると、二項の累乗を簡単な方法で計算できます。
簡単に言えば、ニュートンの二項式は、(a+b) nの形式の代数式を解くことができる式に基づいています。この公式はアイザック ニュートンにちなんで命名されたという事実にもかかわらず、その起源については議論があることは言及する価値があります。
つまり、一部の研究では、中東における二項定理の使用を発見することが示唆されています。
ニュートンの二項式はいつ開発されましたか?
ニュートンの二項定理は、ニュートンの二項定理としても知られ、1665 年に開発され、1676 年に王立協会の役員からの 2 通の手紙で初めて伝えられました。
これらの手紙は、無限級数の数学的研究をより深く理解しようとしたドイツの数学者ゴットフリート・ヴィルヘルム・フォン・ライプニッツへの返答でした。ニュートンは彼の定理の結果を共有し、ライプニッツはそれが求積法または級数で結果を得るのに有用な手法であることを認識しました。
この観察により、ニュートンは有限多項式と同じ方法で無限級数を操作できると結論付けることができました。ニュートンは定理を発表しませんでしたが、英国の数学者ジョン ウォリスは 1685 年に著書『代数』でこの定理を発表し、その創造はニュートンによるものであるとしました。
なぜニュートンの二項式と呼ばれるのでしょうか?
ニュートンの二項式は、 17 世紀に開発した英国の数学者で物理学者のアイザック ニュートンにちなんで名付けられました。ニュートンはこの定理を最初に発見したわけではありませんが、任意の正の整数 n についてその定理が有効であることを証明したのは彼が最初でした。
ニュートンの二項式は、代数学や微積分において非常に便利な数学ツールであり、物理学、統計学、工学、コンピューター サイエンスなどの分野で広く使用されています。
ニュートンの二項公式とは何ですか?
前に述べたように、ニュートンの二項式は二項式のべき乗を求める公式です。上記二項累乗を求めるために、「二項係数」が使用されます。前の用語は、一連の組み合わせを指します。
これを念頭に置くと、ニュートンの二項公式を次のように分解できます。
- (a + b) 2 = a 2 + 2ab + b 2
- (a – b) 2 = a 2 – 2ab + b 2
- (a + b) 3 = a 3 + 3a 2 b + 3 ab 2 + b 3
(a+b) nの展開を参照する数式は注目エンティティと呼ばれ、任意の自然数「n」についてこの演算を表す一般式を得ることができます。
結果として得られる各多項式の係数を調べると、パスカルの三角形として知られるシーケンスに従うことがわかります。
パスカルの三角形のシーケンスは数値 1 で始まり、後続の各行の最後の桁は常に 1 になります。中間値は、計算対象の値のすぐ上にある前の行の 2 つの数値を加算することによって取得されます。
ニュートンの二項式で項を見つけるにはどうすればよいですか?
ニュートンの二項式で特定の項を見つけるには、次の一般式が使用されます。
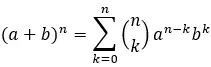
金:
a と b は二項式の係数です。
n は二項式の指数です。
k は、見つけたい特定の用語です。
Σはk=0〜nの和を表す。
[nk] は次の式で計算される二項係数です。
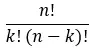
したがって、完全に展開された式は次のようになります。
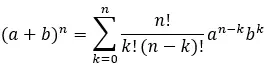
ニュートン二項式の解例
これらの値が見つかると、式に代入され、式が解かれて特定の項が得られます。たとえば、二項 (2x + 3) 6の第 5 項を見つけたい場合は、次のようになります。
1 = 2x
b = 3
n=6
k = 5
したがって、次の式を使用します。
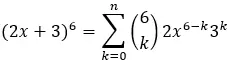
5 番目の項は k=5 に対応するため、次のようになります。
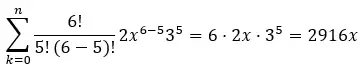
したがって、二項 (2x + 3) 6の第 5 項は 2916x です。
5 次のニュートン二項式とは何ですか?
次数 5 のニュートン二項式は、 (a + b) 5の形式の代数表現です。ここで、「a」と「b」は変数であり、指数 5 は二項式の次数を示します。この式を拡張すると、6 つの項を含む 2 次多項式が得られます。
(a + b) 5 = a 5 + 5a 4 b + 10a 3 b 2 + 10a 2 b 3 + 5ab 4 + b 5
この多項式の各項は、二項式の係数と「a」および「b」の累乗を組み合わせることによって取得されます。たとえば、第 2 項 (5a 4 b) は、二項係数 (5 選択 1 = 5) に「a」の 4 乗と b の 1 乗を乗算して得られます。
次数 5 のニュートン二項式は、統計学、確率論、量子力学など、数学や物理学のさまざまな分野で役立ちます。
ニュートンの二項式はどのように応用できるのでしょうか?
ニュートンの二項式は、次のようなさまざまな分野で幅広く応用できます。
- 確率の計算: 二項定理は、コイン投げや一連のテストの成功または失敗などの二項イベントの確率を計算するために使用されます。
- 数論– ニュートンの二項式は、数論で多項式を拡張し、方程式を単純化するために使用されます。
- 統計: ニュートンの二項分布は、二項分布の計算や信頼区間の構築に使用されます。
- 物理学– 物理学では、二項定理は相対性理論や量子力学などの分野で使用されます。
- 経済学と金融: ニュートンの二項式は、経時的なキャッシュ フローの現在価値と将来価値を計算したり、金融オプションの評価に使用されます。
- プログラミングとコンピューター サイエンス: ニュートンの二項式はアルゴリズム開発とコンピューター プログラミングで使用されます。
ニュートンの二項式が重要なのはなぜですか?
ニュートンの二項式は、代数と数論の発展のための基本的な数学的ツールであるため、関連性があります。二項関数の二乗やその他のべき乗の結果を計算できるため、方程式を解いたり、代数式を簡略化するのに非常に役立ちます。
さらに、統計、確率、物理学などの分野にも応用されています。要約すると、ニュートンの二項式は数学において不可欠な概念であり、これを理解することは多くの研究分野で進歩するために不可欠です。
ニュートンの二項式を表現する他の方法はありますか?
はい、ニュートンの二項式を表現する他の方法があります。たとえば、組み合わせ表記を使用して二項係数で表すことができます。
さらに、オイラーの公式を使用して指数関数や三角関数で表すこともできます。同様に、ルジャンドルの公式を使用したガンマ関数に関しても同様です。これらの代替表現は、さまざまな状況や数学的問題で役立ちます。
ニュートン二項式の例
次に、ニュートンの二項式の適用の簡単な例をいくつか見てみましょう。
例 1: (x + y) 5の展開における次数 3 の項を計算します。
解: (x + y) 5の展開では、第 1 項の係数は 1、第 2 項の係数は 5、第 3 項の係数は 10、第 4 項の係数は 10、第 5 項の係数は 5、第 6 項の係数は 1 です。
したがって、順序 3 の条件は次のようになります。
10x 2および3
例 2: (2x – 1) 4の展開で独立項を見つけます。
解決策: (2x – 1) 4の展開では、独立項は (2x) p (-1) (4-p)の組み合わせで見つかります。ここで、p は (2x) pの指数を作る値であり、 (-1) (4-p)足すと 4 になります。
したがって、独立項は次のようになります。
(2x) 2 (-1) 2 = 4
例 3: (3x – 2y) 6の展開で最高次項を見つけます。
解決策: (3x – 2y) 6の展開における最高次項は、 (3x) p (-2y) (6-p)の組み合わせで見つかります。ここで、p は (3x) pの指数を作る値であり、 (-2y) (6-p)二項次数の 6 に等しい。
したがって、最高次項は次のようになります。
(3x) 3 (-2y) 3 = -216x 3および3