ルーシュ・フレベニウスの定理

このページでは、ルーシェフロベニウスの定理とは何か、そしてそれを使って行列のランクを計算する方法を説明します。また、ルーシェ-フロベニウスの定理を使って段階的に解決される例や演習も見つかります。

ルーシェ・フロベニウスの定理とは何ですか?

ルーシェ-フロベニウスの定理は、線形方程式系を分類する方法です。言い換えれば、ルーシェ・フロベニウスの定理は、方程式系を解くことなく、方程式系の解がいくつあるかを知るために使用されます。

方程式系には 3 種類あります。

システム互換性判定 (SCD):システムには独自のソリューションがあります。
不確定互換システム (ICS):システムには無限の解決策があります。
システム互換性がない (SI):システムには解決策がありません。

さらに、ルーシェ-フロベニウスの定理により、後にクラマーの法則を使用して系を解くことも可能になります。

ルーシェ・フロベニウスの定理の声明

ルーシェ・フロベニウスの定理は次のように述べています。

$\displaystyle \bm{A}$

は、連立方程式の未知数の係数によって形成される行列です。そしてお腹

$\displaystyle \bm{A'}$

、または拡張行列は、連立方程式の未知数の係数と独立項によって形成される行列です。

ルーシェ-フロベニウスの定理を使用すると、行列 A と A’ のランクに応じて、どのタイプの方程式系を扱っているかを知ることができます。

ランク(A) = ランク(A’) = 未知数の場合 ⟶ 互換性のあるシステム (SCD) を決定
ランク(A) = ランク(A’) < 未知数の場合 ⟶ 不確定互換システム (SCI)
範囲(A)の場合
$\bm{\neq}$

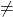
範囲(A’) ⟶ 互換性のないシステム(SI)

ルーシェ-フロベニウスの定理が何を言っているかを理解したら、ルーシェ-フロベニウスの定理の練習問題を解く方法がわかります。以下に 3 つの例を示します。各タイプの連立方程式の定理を使用して解く演習です。

決定された互換システム（SCD）の例

$\begin{cases} 2x+y-3z=0 \\[1.5ex] x+2y-z= 1 \\[1.5ex] 4x-2y+z = 3\end{cases}$

システムの行列 Aと拡張行列 A’ は次のとおりです。

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -3 \\[1.1ex] 1 & 2 & -1 \\[1.1ex] 4 & -2 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -3 & 0 \\[1.1ex] 1 & 2 & -1 & 1 \\[1.1ex] 4 & -2 & 1 & 3\end{array} \right)$

次に、行列 A のランクを計算します。これを行うには、行列全体の行列式が 0 と異なるかどうかを確認します。

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -3 \\[1.1ex] 1 & 2 & -1 \\[1.1ex] 4 & -2 & 1 \end{vmatrix} = 25 \neq 0$

行列には 0 とは異なる 3×3 行列式があるため、行列 A のランクは 3 になります。

$\displaystyle rg(A)=3$

A のランクがわかったら、A’ のランクを計算します。これは、内部に 0 とは異なる次数 3 の行列式があることがわかったばかりなので、少なくともランク 3 になります。さらに、ランク 4 であることはできません。次数 4 の行列式を作成できないため、行列 A’ も階数 3 になります。

$\displaystyle rg(A')=3$

したがって、行列 A のランクは行列 A’ のランクとシステムの未知数 (3) に等しいため、ルーシェフロベニウスの定理により、それが互換性決定システム(SCD) であることがわかります。 :

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

不確定互換システム (ICS) の例

$\begin{cases} x-y+2z=1 \\[1.5ex] 3x+2y+z= 5 \\[1.5ex] 2x+3y-z = 4\end{cases}$

システムの行列 Aと拡張行列 A’ は次のとおりです。

$\displaystyle A= \left( \begin{array}{ccc} 1 & -1 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 2 & 3 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & -1 & 2 & 1 \\[1.1ex] 3 & 2 & 1 & 5 \\[1.1ex] 2 & 3 & -1 & 4 \end{array} \right)$

次に、行列 A のランクを計算します。これを行うには、行列全体の行列式が 0 と異なるかどうかを確認します。

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & -1 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 2 & 3 & -1 \end{vmatrix} = 0$

行列 A 全体の行列式は 0 となるため、ランク 3 ではありません。ランク 2 であるかどうかを確認するには、行列式が 0 とは異なる部分行列を A 内で見つける必要があります。たとえば、左上隅の行列式です。 :

$\displaystyle \begin{vmatrix} 1 & -1 \\[1.1ex] 3 & 2 \end{vmatrix} = 5 \neq 0$

行列には 0 とは異なる 2×2 行列式があるため、行列 A のランクは 2 になります。

$\displaystyle rg(A)=2$

A のランクがわかったら、A’ のランクを計算します。最初の 3 列の行列式が 0 を与えることはすでにわかっているので、他の可能な 3×3 行列式を試します。

$\displaystyle \begin{vmatrix}1 & -1 & 1 \\[1.1ex] 3 & 2 & 5 \\[1.1ex] 2 & 3 & 4\end{vmatrix} = 0 \quad \begin{vmatrix}1 & 2 & 1 \\[1.1ex] 3 & 1 & 5 \\[1.1ex] 2 & -1 & 4\end{vmatrix} = 0 \quad \begin{vmatrix} -1 & 2 & 1 \\[1.1ex] 2 & 1 & 5 \\[1.1ex] 3 & -1 & 4\end{vmatrix} = 0$

行列 A’ の 3×3 行列式はすべて 0 であるため、行列 A’ もランク 3 にはなりません。ただし、内部には 0 とは異なる次数 2 の行列式が含まれています。例:

$\displaystyle \begin{vmatrix} 1 & -1 \\[1.1ex] 3 & 2 \end{vmatrix} = 5 \neq 0$

したがって、行列 A’ はランク 2 になります。

$\displaystyle rg(A')=2$

行列 A の範囲は行列 A’ の範囲に等しいですが、これらはシステムの未知数の数 (3) よりも少ないです。したがって、ルーシェ-フロベニウスの定理によれば、これは不確定互換システム(ICS) です。

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}$

互換性のないシステム（IS）の例

$\begin{cases} 2x+y-2z=3 \\[1.5ex] 3x-2y+z= 2 \\[1.5ex] x+4-5z = 3 \end{cases}$

システムの行列 Aと拡張行列 A’ は次のとおりです。

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -2 \\[1.1ex] 3 & -2 & 1 \\[1.1ex] 1 & 4 & -5 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -2 & 3 \\[1.1ex] 3 & -2 & 1 & 2 \\[1.1ex] 1 & 4 & -5 & 3 \end{array} \right)$

次に、行列 A のランクを計算します。これを行うには、行列全体の行列式が 0 と異なるかどうかを確認します。

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -2 \\[1.1ex] 3 & -2 & 1 \\[1.1ex] 1 & 4 & -5 \end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 2 & 1 \\[1.1ex] 3 & -2 \end{vmatrix} = -7 \neq 0$

行列には 0 とは異なる次数 2 の行列式があるため、行列 A はランク 2 になります。

$\displaystyle rg(A)=2$

A のランクがわかったら、A’ のランクを計算します。最初の 3 列の行列式が 0 になることはすでにわかっているので、たとえば最後の 3 列の行列式を試してみます。

$\displaystyle \begin{vmatrix} 1 & -2 & 3 \\[1.1ex] -2 & 1 & 2 \\[1.1ex] 4 & -5 & 3 \end{vmatrix} = 3 \neq 0$

一方、行列 A’ には結果が 0 とは異なる行列式が含まれているため、行列 A’ のランクは 3 になります。

$\displaystyle rg(A')=3$

したがって、行列 A のランクは行列 A’ のランクより小さいため、ルーシェ-フロベニウスの定理から、それが非互換システム(SI) であると推定します。

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}$

ルーシェ・フロベニウスの定理の問題を解決しました

演習 1

ルーシェ-フロベニウスの定理を使用して、3 つの未知数を含む次の連立方程式のタイプを決定します。

解決策を参照

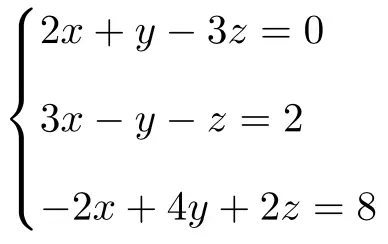
まず、システムの行列 A と拡張行列 A’ を作成します。

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -3 \\[1.1ex] 3 & -1 & -1 \\[1.1ex] -2 & 4 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -3 & 0 \\[1.1ex] 3 & -1 & -1 & 2 \\[1.1ex] -2 & 4 & 2 & 8 \end{array} \right)$

次に、行列 A のランクを見つける必要があります。これを行うには、行列の行列式が 0 と異なるかどうかを確認します。

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -3 \\[1.1ex] 3 & -1 & -1 \\[1.1ex] -2 & 4 & 2 \end{vmatrix} = -4+2-36+6+8-6=-30 \bm{\neq 0}$

0 とは異なる 3 次行列式を持つ行列、行列 A のランクは 3 です。

$\displaystyle rg(A)=3$

A のランクがわかったら、A’ のランクを計算します。これは、内部に 0 とは異なる次数 3 の行列式があることがわかったため、少なくともランク 3 になります。さらに、4×4 の行列式を作成できないため、ランク 4 になることはできません。したがって、行列 A’ もランク 3 になります。

$\displaystyle rg(A')=3$

したがって、ルーシェ-フロベニウスの定理のおかげで、A の範囲が A’ の範囲および未知数の数に等しいため、これが決定互換システム(SCD) であることがわかります。

演習 2

ルーシェ-フロベニウスの定理を使用して、3 つの未知数を含む次の連立方程式を分類します。

解決策を参照

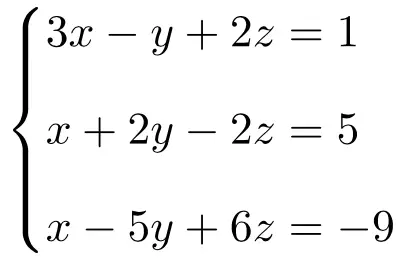
まず、システムの行列 A と拡張行列 A’ を構築します。

$\displaystyle A= \left( \begin{array}{ccc}3 & -1 & 2 \\[1.1ex] 1 & 2 & -2 \\[1.1ex] 1 & -5 & 6 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & -1 & 2 & 1 \\[1.1ex] 1 & 2 & -2 & 5 \\[1.1ex] 1 & -5 & 6 & -9 \end{array} \right)$

次に、行列 A の範囲を計算してみましょう。

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & -1 & 2 \\[1.1ex] 1 & 2 & -2 \\[1.1ex] 1 & -5 & 6 \end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 3 & -1 \\[1.1ex] 1 & 2 \end{vmatrix} = 7 \neq 0$

したがって、行列 A のランクは 2 になります。

$\displaystyle rg(A)=2$

$\displaystyle \begin{vmatrix}-1 & 2 & 1 \\[1.1ex] 2 & -2 & 5 \\[1.1ex] -5 & 6 & -9\end{vmatrix} = 0 \quad \begin{vmatrix}3 & 2 & 1 \\[1.1ex] 1 & -2 & 5 \\[1.1ex] 1 & 6 & -9\end{vmatrix} = 0 \quad \begin{vmatrix} 3 & -1 & 1 \\[1.1ex] 1 & 2 & 5 \\[1.1ex] 1 & -5 & -9\end{vmatrix} = 0$

行列 A’ の 3×3 行列式はすべて 0 であるため、行列 A’ もランク 3 にはなりません。ただし、その内部には 0 とは異なる次数 2 の行列式が多数含まれています。例:

$\displaystyle \begin{vmatrix} -1 & 2 \\[1.1ex] 2 & -2 \end{vmatrix} = -2 \neq 0$

したがって、行列 A’ はランク 2 になります。

$\displaystyle rg(A')=2$

行列 A のランクは行列 A’ のランクに等しいですが、これら 2 つはシステムの未知数の数 (3) よりも小さいです。したがって、ルーシェ-フロベニウスの定理により、これは不確定互換システム(ICS) であることがわかります。

演習 3

ルーシェ-フロベニウスの定理を使用して、次の方程式系がどのようなタイプのシステムであるかを判断します。

解決策を参照

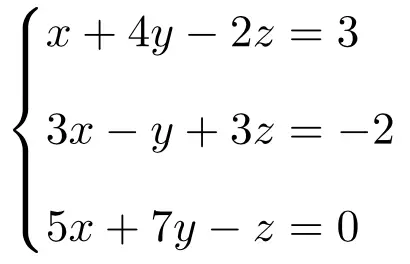
まず、システムの行列 A と拡張行列 A’ を作成します。

$\displaystyle A= \left( \begin{array}{ccc} 1 & 4 & -2 \\[1.1ex] 3 & -1 & 3 \\[1.1ex] 5 & 7 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 4 & -2 & 3 \\[1.1ex] 3 & -1 & 3 & -2 \\[1.1ex] 5 & 7 & -1 & 0 \end{array} \right)$

次に、行列 A の範囲を計算してみましょう。

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 4 & -2 \\[1.1ex] 3 & -1 & 3 \\[1.1ex] 5 & 7 & -1\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 1 & 4 \\[1.1ex] 3 & -1 \end{vmatrix} = -13 \neq 0$

したがって、行列 A のランクは 2 になります。

$\displaystyle rg(A)=2$

A のランクがわかったら、A’ のランクを計算します。最初の 3 列の行列式は 0 を返しますが、最後の 3 列の行列式はそうではないことはすでにわかっています。

$\displaystyle \begin{vmatrix} 4 & -2 & 3 \\[1.1ex]-1 & 3 & -2 \\[1.1ex] 7 & -1 & 0 \end{vmatrix} = -40 \neq 0$

したがって、行列 A’ のランクは 3 になります。

$\displaystyle rg(A')=3$

行列 A のランクは行列 A’ のランクより小さいため、ルーシェ-フロベニウスの定理から、それが非互換システム(SI) であると推定できます。

演習 4

ルーシェ-フロベニウスの定理を使用して、3 つの未知数を含む次の連立方程式のタイプを決定します。

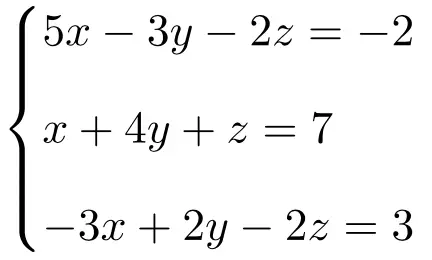
Rouche - 3 つの未知数と 3 つの方程式を使用したフロベニウスの定理の演習を解いた

解決策を参照

まず、システムの行列 A と拡張行列 A’ を作成します。

$\displaystyle A= \left( \begin{array}{ccc} 5 & -3 & -2 \\[1.1ex] 1 & 4 & 1 \\[1.1ex]-3 & 2 & -2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 5 & -3 & -2 & -2 \\[1.1ex] 1 & 4 & 1 & 7 \\[1.1ex]-3 & 2 & -2 & 3 \end{array} \right)$

次に、行列 A のランクを計算する必要があります。これを行うには、Sarrus ルールを使用して行列の行列式を解きます。

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 5 & -3 & -2 \\[1.1ex] 1 & 4 & 1 \\[1.1ex]-3 & 2 & -2 \end{vmatrix} = -40+9-4-24-10-6=-75 \bm{\neq 0}$

0 とは異なる 3 次行列式を持つ行列、行列 A のランクは 3 です。

$\displaystyle rg(A)=3$

したがって、行列 A’ もランク 3 になります。これは常に少なくともランク A であるためであり、4×4 行列式を解決できないためランク 4 になることはあり得ません。

$\displaystyle rg(A')=3$

したがって、ルーシェ-フロベニウスの定理を適用すると、A の範囲が A’ の範囲および未知数の数に等しいため、システムが互換性決定システム(SCD) であることがわかります。

演習 5

ルーシェ-フロベニウスの定理を使用して、次の方程式系がどのようなタイプのシステムであるかを特定します。

解決策を参照

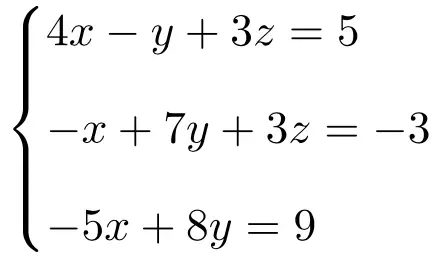
まず、システムの行列 A と拡張行列 A’ を作成します。

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 3 \\[1.1ex] -1 & 7 & 3 \\[1.1ex] -5 & 8 & 0 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 4 & -1 & 3 & 5 \\[1.1ex] -1 & 7 & 3 & -3 \\[1.1ex] -5 & 8 & 0 & 9 \end{array} \right)$

次に、行列 A の範囲を計算してみましょう。

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 3 \\[1.1ex] -1 & 7 & 3 \\[1.1ex] -5 & 8 & 0\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 4 & -1 \\[1.1ex] -1 & 7 \end{vmatrix} = 27 \neq 0$

したがって、行列 A はランク 2 になります。

$\displaystyle rg(A)=2$

A のランクがわかったら、A’ のランクを計算します。すでにわかっている最初の 3 列の行列式は 0 を返しますが、最後の 3 列の行列式は次のようになりません。

$\displaystyle \begin{vmatrix} -1 & 3 & 5 \\[1.1ex] 7 & 3 & -3 \\[1.1ex] 8 & 0 & 9\end{vmatrix} = -408 \neq 0$

したがって、行列 A’ のランクは 3 になります。

$\displaystyle rg(A')=3$

そして最後に、この定義域をルーシェ-フロベニウスの定理に適用します。行列 A の定義域は行列 A’ の定義域より小さいため、非互換システム(SI) になります。

演習 6

ルーシェ-フロベニウスの定理を使用して、次の 3 次方程式系を分類します。

$\begin{cases} 6x-2y+4z=1 \\[1.5ex] -2x+4y+3z= 7 \\[1.5ex] 8x-6y+z = -6\end{cases}$

解決策を参照

まず、システムの行列 A と拡張行列 A’ を構築します。

$\displaystyle A= \left( \begin{array}{ccc} 6 & -2 & 4 \\[1.1ex] -2 & 4 & 3 \\[1.1ex] 8 & -6 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 6 & -2 & 4 & 1 \\[1.1ex] -2 & 4 & 3 & 7 \\[1.1ex] 8 & -6 & 1 & -6 \end{array} \right)$

次に、行列 A の範囲を計算してみましょう。

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 6 & -2 & 4 \\[1.1ex] -2 & 4 & 3 \\[1.1ex] 8 & -6 & 1 \end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 6 & -2 \\[1.1ex] -2 & 4 \end{vmatrix} = 20 \neq 0$

したがって、行列 A のランクは 2 になります。

$\displaystyle rg(A)=2$

$\displaystyle \begin{vmatrix} -2 & 4 & 1 \\[1.1ex]4 & 3 & 7 \\[1.1ex] -6 & 1 & -6\end{vmatrix} = 0 \quad \begin{vmatrix}6 & 4 & 1 \\[1.1ex] -2 & 3 & 7 \\[1.1ex] 8 & 1 & -6\end{vmatrix} = 0 \quad \begin{vmatrix} 6 & -2 & 1 \\[1.1ex] -2 & 4 & 7 \\[1.1ex] 8 & -6 & -6\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 6 & -2 \\[1.1ex] -2 & 4 \end{vmatrix} = 20 \neq 0$

したがって、行列 A’ はランク 2 になります。

$\displaystyle rg(A')=2$

最後に、ルーシェ-フロベニウスの定理を適用すると、行列 A の範囲は行列 A’ の範囲に等しいが、これら 2 つは行列内の未知数の数より小さいため、これが不確定互換システム(ICS) であることがわかります。システム(3):

ルーシェ・フロベニウスの定理とは何ですか?

ルーシェ・フロベニウスの定理の声明

決定された互換システム（SCD）の例

不確定互換システム (ICS) の例

互換性のないシステム（IS）の例

ルーシェ・フロベニウスの定理の問題を解決しました

演習 1

演習 2

演習 3

演習 4

演習 5

演習 6

コメントする 返信をキャンセル

コメントする返信をキャンセル