ワイエルシュトラスの定理

この記事では、ワイエルシュトラスの定理の定義を説明します。さらに、ワイエルシュトラスの定理を段階的に解くいくつかの練習問題を練習して、完全に理解することができます。

ワイエルシュトラスの定理の説明

ワイエルシュトラスの定理によれば、関数が閉じた区間で連続である場合、その関数はその区間で絶対最大値と絶対最小値を持ちます。

➤ 「 連続関数とは何ですか?」を参照してください。

ワイエルシュトラスの定理は、最大値と最小値が存在することのみを述べていますが、これらの点の値を計算することは役に立ちません。

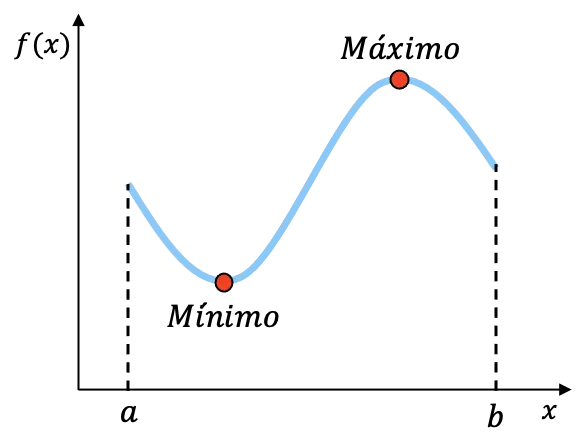
たとえば、上記のグラフの関数は区間 [a,b] で連続しており、この区間に最小値と最大値があります。これら 2 つの点の正確な座標を知ることはできませんが、関数が区間内にこれら 2 つの端点を持つことはわかっています。

➤参照: 関数の最大値と最小値を計算する方法

この関数は区間全体にわたって連続しているため、同じ区間にわたって絶対最小値と絶対最大値の間のすべての可能な値を取ることになります。

さらに、ワイエルシュトラスの定理の結果として、閉区間上の任意の連続関数はの上下に制限され、関数の上限と下限はそれぞれ絶対最大値と絶対最小値であると推測できます。

数学的には、ワイエルシュトラスの定理は次のように表現できます。

金

そして

閉区間に含まれる 2 つの点 (それぞれ絶対最小値と絶対最大値)

関数が定義されています。

ワイエルシュトラスの定理の証明は非常に複雑で、概念にはあまり寄与しないため、この記事では説明しません。重要なことは、ワイエルシュトラスの定理とは何か、そしてそれが何に使用されるのかを理解することです。

ワイエルシュトラスの定理で解決された問題

演習 1

次の関数が提案された間隔に制限されているかどうかを判断します。

➤参照:対数関数の定義域

ワイエルシュトラスの定理を適用することで、関数が区間 [5,10] で制限されているかどうかを判断できます。したがって、関数がこの区間で連続であるかどうかを知る必要があります。これを行うには、対数関数の定義域を計算します。

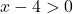
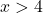
この関数は x=4 より大きいすべての値に対して連続であるため、区間 [5,10] で連続です。

したがって、この関数は区間 [5,10] に関するワイエルシュトラスの定理を満たします。これは、この区間の上下に制限があることを意味します。

演習 2

次の関数に、提案された間隔にわたって最大値および/または最小値があるかどうかを判断します。

➤参照:有理関数の定義域

まず、有理関数の連続性を分析します。

ただし、この関数は x=2 で不連続性を示しており、これは区間 [-3,3] で連続ではないことを意味します。

つまり、この関数はワイエルシュトラスの定理を満たさないため、この区間に最小値があるのか最大値があるのかを判断できません。

演習 3

次の関数が提案された間隔内に最大値および/または最小値を持つかどうかを判断し、これらの点を計算します。

➤参照:2 次関数の特性

二次関数の定義域はすべて実数です。

したがって、この関数は区間 [0,4] で連続であり、ワイエルシュトラスの定理を満たします。したがって、この関数には、この間隔で絶対最小値と絶対最大値が存在します。

さらに、この放物線の頂点は正確に x=0 にあるため、関数は区間 [0,4] で厳密に増加し、その結果、最小値は x=0 で、最大値は x= 4 になります。

カール・ヴァイエルシュトラス

ワイエルシュトラスの定理が何を意味するのかを理解したら、この定理の目録が誰にあるのかを簡単に説明します。

カール・テオドール・ヴィルヘルム・ヴァイエルシュトラスは、19 世紀のドイツの非常に重要な数学者でした。より正確には、1815 年 10 月 31 日にオステンフェルデで生まれ、1897 年 2 月 19 日にベルリンで亡くなりました。

ワイエルシュトラスの定理に加えて、彼は数学への他の貢献でも知られています。その中で、彼は関数の 3 つの非常に重要な概念である連続性、極限、導関数の定義を与えました。

同様に、彼はボルツァーノ・ヴァイエルシュトラスの定理、平均値の定理、ハイネ・ボレルの定理など、当時まだ数学的に検証されていなかった特定の定理を実証することに成功しました。

興味深いことに、月のクレーターとヴァイエルシュトラスに敬意を表して彼にちなんで名付けられた小惑星があります。