このページでは、平面 (R2) 内の 2 つの線の相対位置を決定するために存在するさまざまな方法について説明します。さらに、いくつかの例が表示され、段階的に問題を解いて練習することができます。
平面内の 2 本の線の相対位置は何ですか?
平面内の 2 つの線の間の相対位置を調べる前に、明らかに線が何であるかを正確に知る必要があります。それはline の定義で見つけることができます。
したがって、(R2 で) 2 次元で作業する場合、2 つの線の間には 3 種類の相対位置が考えられます。
交差する線

2 つの交差する線には 1 つの共通点しかありません。
平行線

2 本の線は、共通点がなければ平行です。つまり、彼らが決して交差しない場合です。
一致する線

すべての点が共通している場合、2 つの直線は同じです。
一方、平面内の 2 本の線の間の角度は、それらの相対位置にも依存します。
- 交差する線は、0 度 (含まれない) から 90 度 (両端の値を含む) の間の角度で交差します。さらに、それらがちょうど 90 度の直角を形成する場合、それは 2 つの線が垂直であることを意味します。
- 平行線は方向が同じなので、角度は 0°になります。
- また、同じ理由で、一致する線の間の角度も 0 度になります。
2 本の線の間の角度がどのように計算されるかを知りたい場合は、 2 本の線の間の角度の公式を確認してください。ここでは、2 つの線の間の角度を決定する方法の詳細な説明、いくつかの例、さらには演習を行って概念を完全に理解できるようにします。
平面内の 2 つの線の相対位置を見つける方法
2 次元空間内の 2 つの線の間の相対位置を知ることは、線がどのように表現されるかによって異なります。
- 線の方向ベクトル: 2 つの線が異なる方向ベクトルを持つ場合、それらは交差する必要があります。一方、方向ベクトルの座標が等しいか比例している場合は、平行または一致する可能性があります(共通点があるかどうかを確認する必要があります)。
- 明示的な方程式: 2 本の直線の傾きが異なる場合
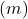
逆に、線の傾きが同じで原点の順序が異なる場合は、
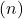
それらは平行です。最後に、2 つの線が元々等しい傾きと縦座標を持っている場合、これらの線は混同されます。
- 一般 (または暗黙の) 方程式:非比例係数 A および B を持つ 2 本の直線は常に交差します。ただし、これら 2 つのパラメータが相互に比例するが、係数 C には比例しない場合、それらは平行になります。そして最後に、3 つの項が比例する場合、これは直線が混乱していることを意味します。
上の直線の方程式に疑問がある場合は、 平面内の直線の方程式の説明を参照してください。ここでは、すべての直線方程式の公式、その計算方法、例題と直線方程式の演習問題を見つけることができます。
次の表に、前述のプロパティの概要を示します。

次に、2 つの線の間の相対位置を決定する方法の 2 つの例を見ていきます。
例1
- 明示的な方程式の形式で定義された次の 2 つの直線の間の相対位置を求めます。
![]()
2 つの直線は同じ傾きを持っています。
![]()
ただし、オリジンには異なるコンピューターがあります。
![]()
したがって、傾きは同じですが切片が異なるため、線は平行になります。
例 2
- 暗黙的な (または一般的な) 方程式で表される次の 2 つの直線の間の相対位置を決定します。
![]()
両方の直線は明示的な方程式として表現されるため、それらの係数のいずれかが比例するかどうかを確認する必要があります。
![]()
線の 3 つの項は比例しているため、線は一致します。
連立方程式を使用して、平面内の 2 つの直線の相対位置を決定します。
2 つの直線間の相対位置を知るもう 1 つの方法は、直線の方程式によって形成される連立方程式を分析することです。
- システムに固有のソリューションがある場合、線は交差します。さらに、2 つの直線の交点がシステムの解になります。
- 解のない系の場合、これは線分に共通点がなく、したがって平行線であることを示します。
- システムに無限に多くの解がある場合、これは線分がすべての共通点を持ち、したがって線分が交差していることを意味します。
例 3
- 連立方程式を使用して、次の 2 つの直線の相対位置を計算します。
![]()
2 つの直線の相対位置を見つけるには、2 つの直線によって形成される次の連立一次方程式を解く必要があります。
![Rendered by QuickLaTeX.com \left.\begin{array}{l} 3x+4y+5=0\\[2ex] 5x+y-3=0\end{array}\right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-243b1e787e6532fbafbfca53d934f4ad_l3.png)
この場合は代入法で系を解きます。したがって、変数を分離します
![]()
2 番目の式から得た値を最初の式に代入します。
![Rendered by QuickLaTeX.com \left.\begin{array}{l} 3x+4y+5=0\\[2ex] 5x+y-3=0\end{array}\right\} \begin{array}{l} \\[2ex] \longrightarrow \ y=3-5x \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ad3456c92c838f40d60afdb45e1eb2f3_l3.png)
![]()
![]()
![]()
![]()
![]()
そして、未知のものにどれだけの価値があるかがわかれば、
![]()
その値を、見つかった式に代入します。
![]()
![]()
![]()
したがって、2 つの直線で構成される連立方程式の解は 1 つだけ得られるため、 2 つの直線は交差します。そして、それらが交差する点がシステムの解、つまり点です。
![]()
平面内の 2 つの線の相対位置の問題を解決しました
演習 1
次の線が交差しているか、平行であるか、一致しているかを判断します。
![]()
どちらの直線も暗黙的な (または一般的な) 方程式として表現されるため、それらの係数のいずれかが比例するかどうかを確認する必要があります。
![]()
直線の係数 A と B のみが相互に比例し、係数 C には比例しません。したがって、 2 つの直線は平行です。
演習 2
パラメトリック方程式として表される次の 2 つの直線間の相対位置を求めます。
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=4-5t \\[2ex] y= 1+3t \end{cases}\qquad \qquad s: \ \begin{cases} x=-2t \\[2ex] y=6+9t \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bafb951a2141722b0bbb7a1681f506ea_l3.png)
2 本の直線によって形成される連立方程式を解くと、それらの相対位置を見つけることができます。ただし、それらはパラメトリック方程式の形式であるため、方向ベクトルを簡単に見つけることができ、それらが比例しない場合は、線が交差していることを意味します。この場合、方程式系全体を解くのにそれほど時間はかかりません。
各ラインの方向ベクトルのデカルト座標がパラメータの前の数字になるようにします。
![]()
![]()
方向ベクトルがわかったら、その比例性を確認します。
![]()
方向ベクトルは比例しないため、線は互いに交差します。
演習 3
次の線が交差しているか、平行であるか、一致しているかを示し、(該当する場合) それらの間の交点も見つけます。
![]()
2 つの直線は明示的な方程式によって定義され、異なる傾きを持っています。
![]()
傾きが異なるため、線は交差します。
したがって、線が交差するため、共通点が 1 つあり、それを計算するには、2 つの線によって形成される連立方程式を解く必要があります。
![Rendered by QuickLaTeX.com \left.\begin{array}{l} y=4x-5\\[2ex] y=-2x+7\end{array}\right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b3923ff74a214543ddd2cc44a42e3813_l3.png)
この場合、等化法を使用してシステムを解きます。
![]()
はすでに削除されています:
![]()
![]()
![]()
![]()
![]()
そして未知のものを手に入れたら
![]()
その値を任意の式に置き換えます
![]()
どれくらいの価値があるかを調べるには:
![]()
![]()
したがって、2 つの線の交点はシステムの結果です。
![]()
演習 4
未知数の値を計算する
![]()
そして
![]()
次の 2 つの線が平行になるようにします。
![]()
線は一般的な (または暗黙的な) 方程式形式で記述されます。したがって、2 つの直線が平行であるためには、それらの係数 A と B が比例する必要があります。つまり、次の方程式が満たされる必要があります。
![]()
したがって、未知の値を取得するには、前の式を解く必要があります。
![]()
これを行うには、分数を横方向に乗算します。
![]()
![]()
![]()
一方、線が平行であるためには、その独立項が他の係数に比例することはありません。
![]()
したがって、前と同様に、分数を横に乗算して不等式を解決します。
![]()
![]()
![]()
つまり、2本の直線が平行になるように、
![]()
2でなければなりません、そして
![]()
3 を除く任意の実数を指定できます。
演習 5
直線に平行な直線の明示的な方程式を求めます。
![]()
そしてその点で何が起こるか
![]()
まっすぐであること
![]()
![]()
線が線と平行になるように
![]()
両方とも同じ傾きを持つ必要があります。そして線の傾き
![]()
は 2:
![]()
したがって、見つける必要がある直線の方程式は次のようになります。
![]()
線の傾きがわかれば、その線に属する点を線の方程式に代入することで y 切片を計算できます。
![]()
![]()
![]()
![]()
![]()
したがって、この直線の明示的な方程式は次のようになります。
![]()
ここまでできたということは、計画内の 2 つの線の間の相対的な位置をすでにマスターしていることを意味します。よくやった!
しかし、多くの人が疑問に思っていることの 1 つは…2 つの線の間の相対位置を知ることに何の意味があるのでしょうか?
2 つの線の間の距離の計算は相対的な位置に依存するため、線間の相対位置の応用の 1 つは、2 つの線の間の距離を知ることができることです。
- 線が交差するか一致する場合、距離はゼロになります。
- 一方、線が平行の場合は、特定の公式を適用する必要があります。さらに興味がある場合は、2 本の平行線の間の距離がどのように計算されるかを確認してください。