ここでは、正接関数がどのように導出されるかを説明します。さらに、接線の導関数の例を確認したり、段階的に解決される演習で練習したりすることもできます。最後に、正接微分公式を示し、逆正接微分公式も示します。
タンジェントの導関数は何ですか?
x のタンジェントの導関数は、x のコサインの 2 乗で 1 に等しくなります。 x のタンジェントの導関数は、x の正割の 2 乗、および x のタンジェントの 2 乗に 1 を加えたものと等価です。
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{tan}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{1}{\text{cos}^2(x)}=\text{sec}^2(x)=1+\text{tan}^2(x)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dfb81626a982a908c4e517b1ecb748e7_l3.png)
すべての式は同等であるため、正接関数を導出する可能な式は 3 つあります。
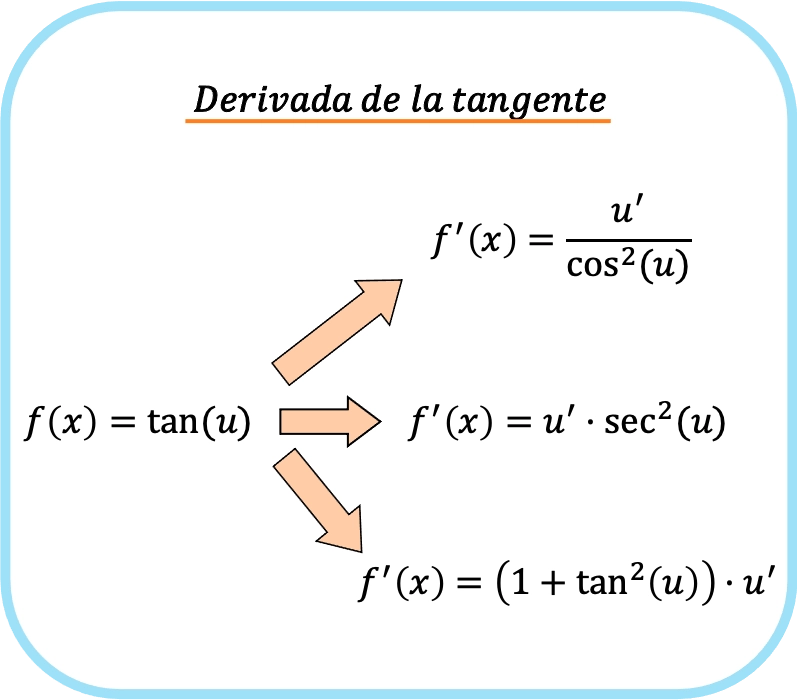
一方、接線引数に x とは異なる関数がある場合 (これを u と呼びます)、連鎖規則を適用する必要があります。したがって、u のタンジェントの導関数は次のようになります。
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{tan}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{u'}{\text{cos}^2(u)}=\text{sec}^2(u)\cdot u'=\left(1+\text{tan}^2(u)\right)\cdot u'\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1ad272ab857ecf57ebc79e68a4370fc5_l3.png)
つまり、接線導関数ルールは次のように要約できます。
接線導関数の例
正接導関数の公式を考慮して、このセクションでは、正接関数の導出方法を理解できるように、このタイプの三角関数導関数のいくつかの例を解きます。
例 1: 2x の正接の導関数
![]()
正接の導関数を計算するには、上で見た 3 つの公式のいずれかを使用できます。この場合、コサイン公式を使用します。
![]()
関数 2x は線形なので、導関数は 2 です。したがって、2x のタンジェントの導関数は 2x のコサインの 2 乗で 2 になります。
![]()
例 2: x の 2 乗の正接の導関数
![]()
この例では、正接引数関数は x ではなく、導関数を持つ関数です。つまり、それを導出するには連鎖規則を適用する必要があります。
![]()
x の 2 乗の導関数は 2x であるため、x 2の正接の導関数は次のようになります。
![]()
例 3: 立方体の接線の導関数
![]()
この問題では合成関数があるため、接線を微分するために連鎖規則も使用する必要があります。
![]()
さらに、タンジェントは 3 乗されます。つまり、タンジェントの微分の公式を適用する前に、べき乗の公式を使用する必要があります。
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)&=3\text{tan}^2(9x^2-4x)\cdot \cfrac{18x-4}{\text{cos}^2(9x^2-4x)} \\[2ex]&=\cfrac{3\text{tan}^2(9x^2-4x)\cdot(18x-4)}{\text{cos}^2(9x^2-4x)}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-424a7372a1d97a5c17a86d6253666164_l3.png)
逆正接の導関数
他の逆関数と同様に、正接関数には逆正接関数という逆関数もあります。これを導出する公式はタンジェントの公式とは似ていませんが、場合によっては役立つ可能性があるため紹介します。
関数の逆正接の導関数は、関数の導関数を 1 で割った商に、その関数の 2 乗を加えた商です。
![]()
たとえば、3x の逆正接の導関数は次のようになります。
![]()
接線の微分に関する演習を解決しました
次の正接関数の導関数を計算します。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
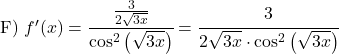
接線の導関数の証明
これが架空の式ではないことを確認できるように、このセクションではタンジェントの数学的定義を使用してタンジェントの導関数の公式を示します。
これを行うには、3 つの三角比を接続する三角恒等式から開始します。
![]()
除算の導関数の公式を使用すると、導関数は次のようになります。
![]()
![]()
![]()
しかし、基本的な三角関数の恒等式を使用すると、サインの 2 乗とコサインの 2 乗を加算したものが 1 であることがわかります。
![]()
![]()
そして、私たちはすでに接線の導関数の最初の公式に到達しています。さらに、セカントはコサインの逆乗であるため、2 番目の式も導出されます。
![]()
最後に、接線導関数の 3 番目の規則は、前のステップの分数を分数の合計に変換することで証明できます。
![]()
![]()
![]()