このページでは、パスカルの三角形とも呼ばれるタルターリアの三角形とは何かについて説明します。タルターリア (またはパスカル) 三角形を数学的に構築する方法と、それが何に使用され、そのすべての特性が何であるかを学びます。最後に、この非常に重要な三角形がいつどのようにして生まれたのかを示します。
タルターリア (またはパスカル) の三角形とは何ですか?
タルターリアの三角形 は、パスカルの三角形とも呼ばれ、三角形の形で順序付けられた整数を数学的に表現したものです。タルターリア (またはパスカル) 三角形は、数学的な計算を行うために使用されます。
これはタルターリアまたはパスカルの三角形の定義ですが、三角形のイメージを使用すると、概念をよりよく理解できるはずです。
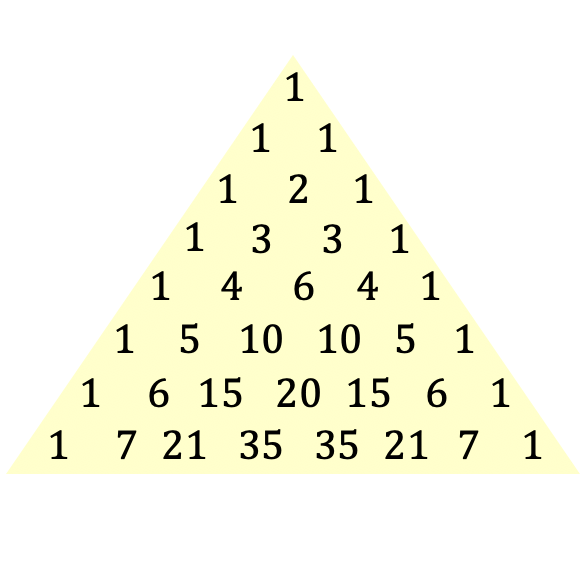
タルターリアの三角形は、1654 年にこの三角形の表現を導入したフランスの哲学者で数学者のブレーズ パスカルにちなんでパスカルの三角形とも呼ばれますが、この三角形は古くから知られていました。以下では、この特定の三角形の歴史を詳しく掘り下げていきます。
タルターリアやパスカルの三角形はどのように構築されますか?
パスカルの三角形 (またはタルターリア) で見たように、たくさんの数字がありますが、それは暗記する必要があるという意味ではありません (ありがたいことに)。パスカルまたはタルターリアの三角形のすべての数値を簡単に見つけることができる公式があります。単純な合計を解くだけで済みます。
タルターリアまたはパスカルの三角形を作成するには、三角形の上部 (常に 1) から開始し、次に下の線が計算されます。次の行の各数値は、行の終端が常に 1 である場合を除き、そのすぐ上にある 2 つの数値の合計です。

したがって、数字を足していくことで次々に線を追加できるので、タルターリア三角形の線を好きなだけ計算することができます。
タルターリアの三角形やパスカルの三角形は何に使われますか?
タルターリア三角形の作り方を知るのはとても良いことですが…この算術三角形は何に使われるのでしょうか?さて、タルターリア (またはパスカル) の三角形は、数学、特に代数学の分野で多くの用途があります。
組み合わせ数
まず、タルターリア三角形は、二項係数とも呼ばれる組み合わせ数を直接計算するために使用されます。これらのタイプの操作が何であるかわからない場合は、当社の Web サイト (右上に検索エンジンがあります) でそれらを検索できます。これは、それらがどのように解決されるかを説明する詳細な記事を書いているためです。また、段階的に解決される例や演習も見つかります。しかし、要約すると、組み合わせ数の代数式は次のようになります。
![]()
次の図に示すように、各二項係数の解はこの三角式の数値と等価であるため、すべての組み合わせ数はタルターリア三角形を使用して簡単に決定できます。

たとえば、組み合わせ数
![]()
タルターリア三角形には代わりに 6 があるため、6 を返します。
したがって、タルターリアまたはパスカルの三角形の作成方法を知っていれば、公式を使用せずに、あらゆる組み合わせ数をすばやく計算できます。
ニュートンの二項式
タルターリア (またはパスカル) 三角形のもう 1 つの用途は、二項式の累乗を計算できることです (二項式が何であるかを確認するには、このリンクをクリックしてください)。
二項の強化の例としては、次のような注目すべき恒等があります。
![]()
顕著な恒等式は、多くの計算を節約し、複雑な演算を直接かつ迅速に解決できるため、数学にとって非常に重要です。そのため、Notable Identities が何なのかまだわからない場合は、次のリンクを確認することをお勧めします。
前のリンクで見たように、注目すべき製品はその公式で直接解くことができます。しかし…ペアを 3 乗以上に上げるとどうなるでしょうか?
![Rendered by QuickLaTeX.com \begin{array}{c} (a+b)^3 = \ ? \\[3ex] (a+b)^4 = \ ? \\[3ex] (a+b)^5 = \ ? \\[3ex] \bm{\vdots} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5b0a3cca7974eff9ac7a93f3178897c5_l3.png)
これらの二項式は、 二項定理(またはニュートンの二項式) のおかげで、タルターリアの三角形を使用する非常に簡単な方法で計算できます。一度この方法をマスターすればすぐに応用できますが、それをうまく説明するにはページ全体が必要です。したがって、このタイプの二項式の解き方に興味がある場合は、リンクされたページをクリックすると、その解き方を確認できます。
組み合わせ論
タルターリアの三角形またはパスカルの三角形は、組み合わせと確率を決定するために使用することもできます。
順序に関係なく、グループからいくつの異なるグループを作成できるかを決定する必要がある問題に遭遇した場合は、タルターリアの三角形を使用できます。
たとえば、カードが 5 枚ある場合、3 つを選択できる方法が何通りあるかを知るには、タルターリアの三角形の 5 行目 (最初の行も 0 行目) の 3 列目 (最初の列は 0) に移動するだけです。この位置の数字 (10) は、3 枚のカードを選択できる可能性の数に対応します。
![]()
したがって、5 枚のカードから、3 枚のカードからなる 10 の異なるグループを形成できます。
タルターリア三角形またはパスカル三角形の性質
タルターリアの三角形はパスカルの三角形とも呼ばれ、次の特徴があります。
- タルターリア (またはパスカル) 三角形は対称です。つまり、三角形全体を 2 つの等しい正三角形に分割する垂直線が対称軸です。
- パスカルの三角形の任意の直線にあるすべての数値の水平方向の合計は、2 の累乗に等しくなります。

- タルターリア三角形の対角線も重要です。最初の対角線 (外側の対角線) の数字は 1、2 番目の対角線はすべての自然数のシーケンスによって形成され、3 番目の対角線は三角数に対応し、4 番目の対角線は次のように構成されます。正方晶 (または四面体) 数の。
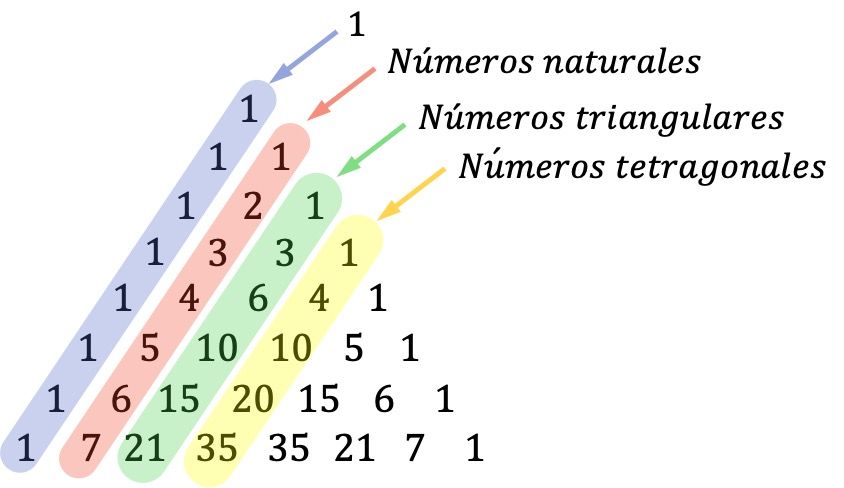
三角数とは、三角形の形で表現できる数のことです。そして、正方晶系の数は三角錐を形成する数です。
三角形または四角形の数が何であるかを知らなければ、何も起こりません。それはタルターリアの三角形についての単なる好奇心です。ただし、自然数(要素を数える数字)の意味を知っておく必要があります。
- 数値 1 を除いて、行の最初の数値が素数の場合、同じ行にあるすべての数値はその数値で割り切れます。たとえば、8 行目 (1-7-21-35-35-21-7-1) では、数字 7、21、および 35 を 7 で割ることができます (7 は素数です)。
- タルターリア三角形のもう 1 つの特徴は、特定の方法で対角線を加算することでフィボナッチ数列を見つけることができることです。
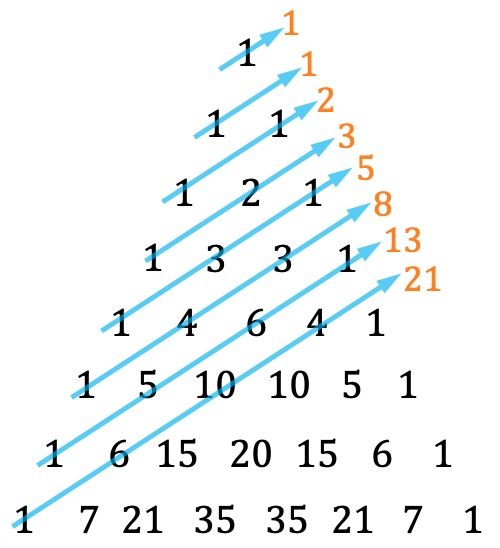
フィボナッチ数列の各項は前の 2 つの項の合計に等しく、最初の 2 つの項は 1 と 1 であることに注意してください。したがって、フィボナッチ数列に属する数値は、1、1、2、3、5、8 となります。 、13、21、34、55、89、144、233、…
- パスカルの三角形の 3 番目の対角線から 2 つの連続する数字 (1-3-6-10-15-…) を加算すると、完全な正方形 (1、4、9、16、25、…) が得られます。
- パスカルの三角形の偶数をある色で塗り、奇数を別の色で塗ると、有名な幾何学集合であるシェルピンスキーの三角形の図形が得られます。以下は、黒の奇数と白の偶数で表された高さ 512 のパスカルの三角形を示しています。

- シングマスター予想では、1 より大きい各数値が出現する回数は有限であると言われています。言い換えると、タルターリアの三角形の行数は無限ですが、1 を除くすべての数字が現れる回数は有限です。興味深いことに、3003 という数字は、三角形内に最大 8 回出現することが現在知られている唯一の数字です。
タルターリアまたはパスカルの三角形の歴史
タルターリアの三角形がどのようなものであるかがわかったので、この非常に特別な数学的な三角形がいつ発明されたかを見てみましょう。
算術三角形の名前は主に有名な科学者タルターリアとパスカルに由来しますが、この代数三角形は以前からすでに使用されていました。
二項係数によって形成された三角形の最初の記録は、10 世紀のインドに遡ります。しかし、ペルシア人、特に数学者のアル・カラジ (953-1029) とオマル・ハイヤーム (1048-1131) はその性質を研究し始めました。これが、イランでそれがハイヤーム・パスカル三角形、または単にハイヤーム三角形として普及した理由です。
この三角形は 11 世紀に数学者の賈賢によって中国に紹介され始めましたが、楊輝が算術三角形として紹介したのは 13 世紀後半になってからです。このため、アジアの国では、それをヤン・フイ・トライアングルと呼んでいます。
数学的三角形は、後にドイツのペトルス・アピアヌスを通じてヨーロッパ大陸に伝わり、具体的には 1527 年に著書『Rechnung』で出版されました。そこから、有名なイタリアの代数学者ニッコロ フォンタナ タルターリアが16 世紀前半にこの三角形を詳しく研究し、イタリアなどの国では彼の名誉を讃えてタルターリアの三角形として知られています。
最後に、フランス人ブレーズ パスカルは、1654 年に出版した『算術三角形に関する論文』で研究した三角形の性質の多くを実証したため、パスカルの三角形と呼ばれるようになりました。これらの特性のいくつかはすでに知られていましたが、数学的帰納法によってそれらの実証を実行したのはパスカルであることに注意してください。