このページでは、線分の中点の意味について説明します。さらに、公式を使用してセグメントの中央を見つける方法も学びます。セグメント中間点の例、演習、および解決済みの問題も表示されます。
セグメントの中点とは何ですか?
数学では、セグメントの中点は、セグメントの端点から同じ距離にある点です。したがって、中央はセグメントを 2 つの等しい部分に分割します。
さらに、中点はセグメントの中心にあるため、セグメントの二等分線に属します。
一方、セグメントの中点は、2 つの幾何学的要素 (セグメントの 2 つの端) から等距離にある点でもあります。
セグメントの中点を計算するにはどうすればよいですか?
セグメントの極点のデカルト座標が与えられると、次のようになります。
![]()
前記セグメントの中央の座標は、極点の座標の半分の合計に対応します。
![]()
これは、デカルト平面 (R2) のセグメントの中央の式です。しかし、明らかに、この式はデカルト空間 (R3) にも適用できます。必要なのは、Z 座標の半分の和を加算することだけです。
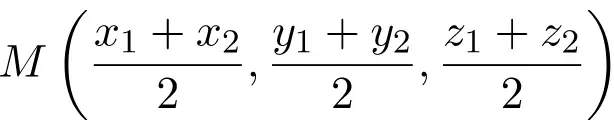
セグメントの中点の座標を計算する方法の例を見てみましょう。
- 次の点によって形成されるセグメントの中点を決定します。
![]()
セグメントの中央を見つけるには、次の式を適用するだけです。
![]()
![]()
![]()
![]()
セグメントの途中で解く演習
演習 1
次の 2 点を端点とする線分の中点は何ですか?
![]()
セグメントの中央を見つけるには、次の式を直接適用する必要があります。
![]()
![]()
![]()
![]()
演習 2
点 A で始まり、中点が M であるセグメントの終点の座標を見つけます。
![]()
この場合、セグメントの始点と中間の座標がわかります。したがって、既知の座標をセグメントの中点の式に代入します。
![]()
![]()
次に、前の式からセグメントの終点の座標を求めます。
X座標
![]()
![]()
![]()
![]()
![]()
Y座標
![]()
![]()
![]()
![]()
![]()
したがって、セグメントの最終端の座標は次のようになります。
![]()
演習 3
次のような平行四辺形があるとします。
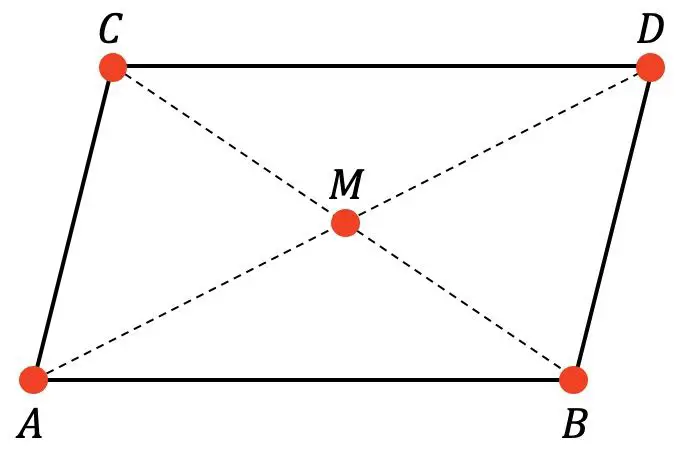
M が平行四辺形の中心であり、点 A、B、C の座標は次のとおりであることがわかります。
![]()
この情報から、中点の公式を使用して、点 D の座標を計算します。
セグメントの中央の公式を使用して点 D の座標を見つけるには、まず点 M の座標を計算し、次に点 D の座標を計算する必要があります。
点 M はセグメント BC の中点であるため、その座標は次のようになります。
![]()
![]()
点 M がわかれば、点 D を見つけることができます。点 M は線分 AD の中央でもあるため、次のようになります。
![]()
点DのX座標
![]()
![]()
![]()
点DのY座標
![]()
![]()
![]()
したがって、点 D の座標は次のようになります。
![]()
演習 4
線分 PQ の中点に垂直な直線の連続方程式を計算します。ポイントになる
![]()
そして
![]()
直線の方程式を決定するには、その方向ベクトルと直線の一部である点が必要です。
この場合、線の方向ベクトルはベクトルに対して垂直になります。
![]()
したがって、ベクトルを計算します
![]()
![]()
そして、他のベクトルに垂直なベクトルを見つけるには、それらの間のベクトルの成分を変更し、成分の符号を変更します。 したがって、次のようになります。
![]()
これで線の方向ベクトルが得られたので、線に属する点が 1 つだけ必要になります。この場合、命令では、線がセグメントの中点を通過することが示されているため、次の式を使用して中点を計算します。
![]()
![]()
最後に、計算された点とベクトルから直線の連続方程式を構築します。
![]()