ここでは、関数の正割を導出する方法を学びます。さらに、正割線の導関数について段階的に解決されるいくつかの演習を確認することができます。最後に、このタイプの三角関数微分の公式のデモンストレーションを示します。
セカントの導関数は何ですか?
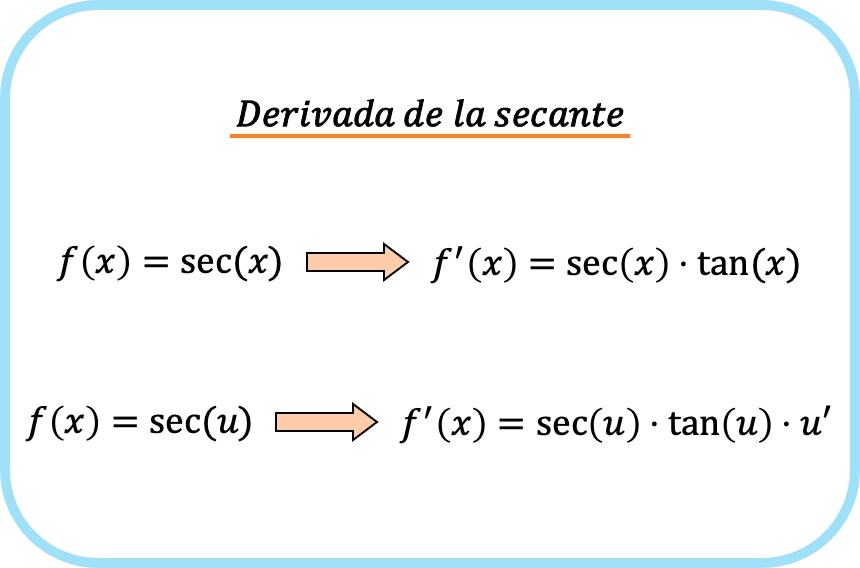
x の正割の導関数は、x の正割と x の正接の積に等しくなります。
![]()
三角関数の公式を適用すると、x の正割の導関数は、x のサインを x のコサインの 2 乗で割った商として定義することもできます。
![]()
連鎖則を適用すると、関数の正割の導関数は、関数の正割と関数の正接と関数の導関数の積になります。
![]()
要約すると、セカント関数の導関数の公式は次のとおりです。
セカントの導関数の例
セカントの導関数の公式が何であるかを理解したら、このタイプの三角関数導関数のいくつかの例を解きます。
例 1: 2x の正割の導関数
この例では、2x のセカントの導関数がどれだけの価値があるかを確認します。
![]()
2x 関数の正割を求めるには、対応する式を使用する必要があります。また、正割引数には x 以外の関数があるため、連鎖規則を適用する必要があります。
![]()
関数 2x は線形なので、導関数は 2 です。したがって、導関数を求めるには、次の式で u を 2x に、u’ を 2 に置き換えるだけです。
![]()
例 2: x の 2 乗の正割の導関数
この演習では、x の 2 乗の正割の導関数が何かを確認します。
![]()
関数のセカントを求めるには、上記の 2 つの公式のいずれかを使用できますが、この場合は、セカントとタンジェントの乗算の公式を使用して関数を微分します。
![]()
x の 2 乗の導関数は 2x となるため、x の二乗の正割の導関数は次のようになります。
![]()
例 3: 多項式の正割 3 乗の導関数
![]()
関数の正割の微分の規則は次のとおりです。
![]()
しかし、この場合、割線は 3 乗され、さらにその引数には多項式関数があるため、複合関数を導出する必要があります。したがって、関数全体を区別するには、連鎖ルールを適用する必要があります。
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)& =3\text{sec}^2(x^5+4x^2-3)\text{sec}(x^5+4x^2-3)\text{tan}(x^5+4x^2-3)(5x^4+8x)\\[1.5ex]&=3\text{sec}^3(x^5+4x^2-3)\text{tan}(x^5+4x^2-3)(5x^4+8x)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7ab88cc23ab3fb559e2386cd52637082_l3.png)
セカントの微分に関する演習を解決しました
次の割線関数を導出します。
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{B) }f(x)& =4\text{sec}^3(5x^4)\cdot \text{sec}(5x^4)\cdot \text{tan}(5x^4)\cdot 20x^3\\[1.5ex] &=4\text{sec}^4(5x^4)\cdot \text{tan}(5x^4)\cdot 20x^3\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-72985d8bce95d808b9070bc7b834b271_l3.png)
![]()
![]()
![]()
セカントの導関数の公式のデモンストレーション
次に、セカントの導関数の公式を証明します。証明を暗記する必要はないことは明らかですが、公式がどこから来たのかを理解しておくことは常に良いことです。
数学的には、セカントの定義はコサインの逆乗です。
![]()
したがって、商ルールを使用して正割を導出してみることができます。
![]()
そして、最初のセクションで見たように、前の式は正割の導関数の式に変換できます。これを行うには、分数を 2 つの異なる分数に分割します。
![]()
サインをコサインで割るとタンジェントに相当するため、商をタンジェントで置き換えます。
![]()
セカント関数の数学的定義によれば、コサインはその逆乗法です。したがって、コサインで割ったものを正割で置き換えると、その導関数の式が得られます。
![]()