この記事では、関数のコタンジェントを導出する方法を見ていきます。コタンジェントの導関数の例や、段階的に解決される演習も見つかります。最後に、コタンジェントの導関数の公式を証明します。
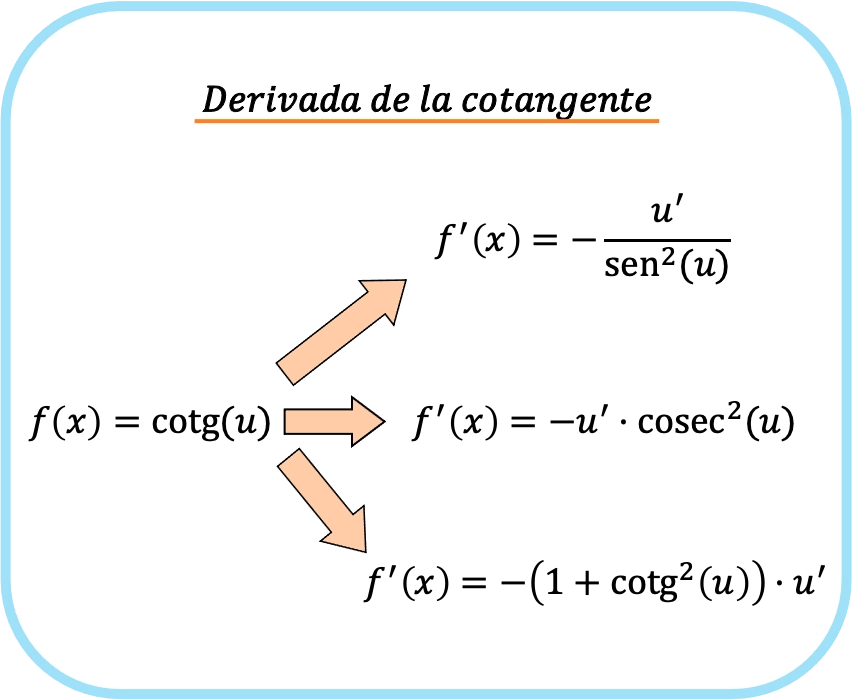
コタンジェントの導関数の公式
x の余接の導関数は、x の正弦の 2 乗の負の 1 に等しくなります。 x のコタンジェントの導関数は、x のコセカントの 2 乗を引いたもの、および 1 と x のコタンジェントの 2 乗を足した合計を引いたものにも等しくなります。
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{cotg}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=-\cfrac{1}{\text{sen}^2(x)}=-\text{cosec}^2(x)=-\left(1+\text{cotg}^2(x)\right)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0a3653f5c765d773ebc789107bf1a825_l3.png)
引数のコタンジェントが x 以外の関数である場合、関数のコタンジェントの導関数の式は前の式と同じですが、式に引数の関数の導関数を乗算します。
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{cotg}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=-\cfrac{u'}{\text{sen}^2(u)}=-u' \cdot \text{cosec}^2(u)=-u' \cdot \left(1+\text{cotg}^2(u)\right)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-38ea1d1edeaf5664c56a946b5a87577d_l3.png)
これは、コタンジェントの導関数を求めるための 3 つの異なる公式があることを意味します。ただし、論理的には、3 つの公式をすべて使用する必要はなく、好みの公式を使用してそれを導き出すことができます。
コタンジェントの導関数の例
関数のコタンジェントの導関数の公式を見てきたので、このセクションでは、このタイプの三角関数の導関数のいくつかの例を解きます。
例 1: 2x の余接の導関数
この例では、関数 2x のコタンジェントの導関数が何かを見ていきます。
![]()
これまで見てきたように、コタンジェントの導関数を計算するには、上記の 3 つの公式のいずれかを使用できます。この場合、正弦波の公式を使用します。
![]()
2x は 1 次項であるため、その導関数は 2 です。したがって、2x のコタンジェントの導関数は、2x の正弦の 2 乗で割った負の 2 になります。
![]()
例 2: x の 2 乗の余接の導関数
2 番目の例では、x の 2 乗の余接の導関数が何であるかを決定します。
![]()
この例では、余接引数の関数は x ではないため、連鎖規則を適用して余接を微分する必要があります。
![]()
x の 2 乗の導関数は 2x であるため、x 2のコタンジェントの導関数は次のようになります。
![]()
例 3: コタンジェントの 3 乗の導関数
最後に、多項式関数の余接の 3 乗の導関数はいくらかを求めます。
![]()
この場合、関数の合成があるため、余接の導関数を求めるには、べき乗の導関数の式で連鎖律を使用する必要があります。
![]()
コタンジェントの微分に関する演習を解決しました
次の余接関数の導関数を計算します。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
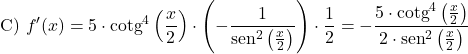
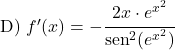
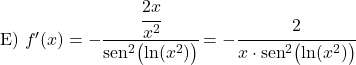
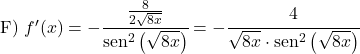
コタンジェントの導関数の証明
この最後のセクションでは、コタンジェントの導関数の公式を示します。これを行うには、コタンジェント関数の数学的定義から始めます。コタンジェント関数は、コサインをサインで割ったものに等しいです。
![]()
ここで、商の導関数のルールを適用して関数を微分します。
![]()
![]()
![]()
分母の共通因数をとり、分数から負の符号を取り除きます。
![]()
![]()
一方、基本的な三角関数の恒等性のおかげで、サインの 2 乗とコサインの 2 乗を足したものは 1 に等しいことがわかっています。
![]()
![]()
こうして、コタンジェントの導関数の最初の式が得られました。同様に、コセカントはサインの逆乗であるため、コタンジェントの導関数の 2 番目の規則も証明されます。
![]()
最後に、この三角関数の導関数の 3 番目の公式は、前のステップの分数を分数の合計に変換することで証明できます。
![]()
![]()
![]()