クラマーの法則 - マソリティ

このページでは、クラマーの法則とは何かを説明し、さらに、クラマーの法則によって連立方程式を解く例と演習も示します。

クラマーの法則とは何ですか?

クラマーの法則は、行列式によって連立方程式を解くために使用される方法です。それがどのように使用されるかを見てみましょう:

連立方程式を考えてみましょう。

$\begin{cases} ax+by+cz= \color{red}\bm{j} \\[1.5ex] dx+ey+fz=\color{red}\bm{k} \\[1.5ex] gx+hy+iz = \color{red}\bm{l} \end{cases}$

システムの行列 A と拡張行列 A’ は次のとおりです。

$\displaystyle A= \left( \begin{array}{ccc} a & b & c \\[1.1ex] d & e & f \\[1.1ex] g & h & i \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} a & b & c & \color{red}\bm{j} \\[1.1ex] d & e & f & \color{red}\bm{k} \\[1.1ex] g & h & i & \color{red}\bm{l} \end{array} \right)$

クラマーの法則によれば、連立方程式の解は次のようになります。

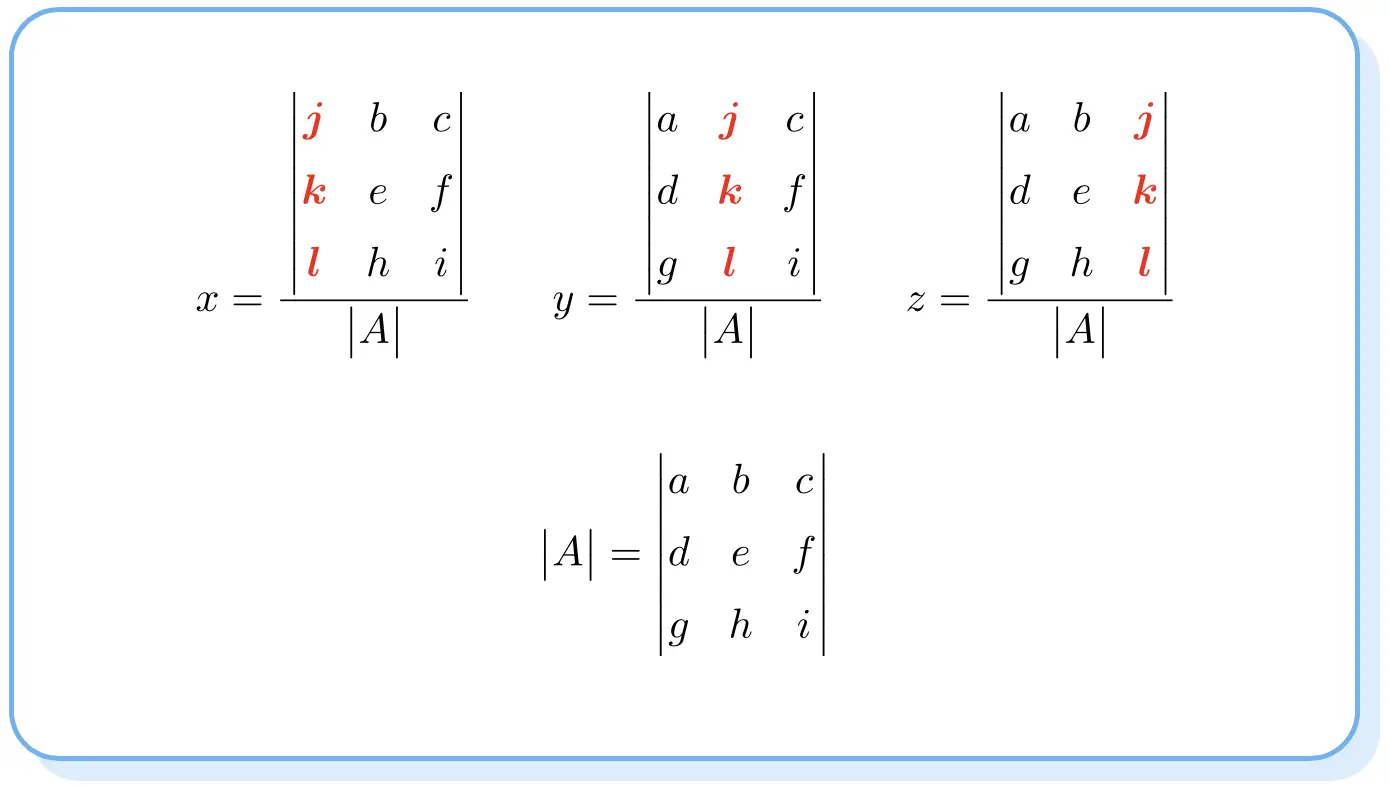
分子の行列式は行列 A の行列式に似ていますが、それぞれの未知数の列が独立項の列に変更されていることに注意してください。

したがって、連立一次方程式を解くためにクラマーの法則が使用されます。しかし、すでにご存知のとおり、連立方程式を解く方法は数多くあります。たとえば、ガウスジョルダンの方法はよく知られています。

以下は、クレイマーの法則、またはクレイマーの法則と呼ばれることもある、連立一次方程式を解く例です。

例 1: 決定された互換性のあるシステム (SCD)

Cramer の法則を使用して、3 つの未知数を含む次の 3 つの方程式系を解きます。

$\begin{cases} 2x+y+3z= 1 \\[1.5ex] 3x-2y-z=0 \\[1.5ex] x+3y+2z = 5\end{cases}$

まず、システムの行列 A と拡張行列 A’ を作成します。

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & 3 & 1 \\[1.1ex] 3 & -2 & -1 & 0 \\[1.1ex] 1 & 3 & 2 & 5 \end{array} \right)$

次に、システムのタイプを確認するために、2 つの行列のランクを計算します。 A のランクを計算するには、行列全体の 3×3 行列式を (Sarrus の規則を使用して) 計算し、それが 0 になるかどうかを確認します。

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{vmatrix} =-8-1+27+6+6-6 = 24 \neq 0$

A の行列式は 0 ではないため、行列 A のランクは 3 になります。

$\displaystyle rg(A)=3$

したがって、行列 A’ もランク 3 になります。ランク 4 にすることはできず、少なくとも行列 A と同じランクでなければなりません。

$\displaystyle rg(A')=3$

行列 A の範囲は、行列 A’ の範囲とシステムの未知数の数 (3) に等しいため、ルーシェ-フロベニウスの定理により、それが決定された互換性のあるシステム(SCD) であることがわかります。

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

システムが SCD であることがわかったら、それを解決するためにCramer の法則を適用します。これを行うには、行列 A、その行列式、および行列 A’ が次のとおりであることを思い出してください。

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & 3 & \color{red}\bm{1} \\[1.1ex] 3 & -2 & -1 & \color{red}\bm{0} \\[1.1ex] 1 & 3 & 2 & \color{red}\bm{5} \end{array} \right)$

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{vmatrix} =24$

未知のものを計算するには

$\displaystyle x$

Cramer の規則を使用して、A の行列式の最初の列を独立項の列で変更し、それを A の行列式で割ります。

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} \color{red}\bm{1} & 1 & 3 \\[1.1ex] \color{red}\bm{0} & -2 & -1 \\[1.1ex] \color{red}\bm{5} & 3 & 2 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{24}{24} = \bm{1}$

未知のものを計算するには

$\displaystyle y$

Cramer の規則を使用して、A の行列式の 2 番目の列を独立項の列で変更し、それを A の行列式で割ります。

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 2 & \color{red}\bm{1} & 3 \\[1.1ex] 3 & \color{red}\bm{0} & -1 \\[1.1ex] 1 & \color{red}\bm{5} & 2\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{48}{24} = \bm{2}$

計算する

$\displaystyle z$

Cramer の規則を使用して、A の行列式の 3 番目の列を独立項の列で変更し、それを A の行列式で割ります。

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} 2 & 1 & \color{red}\bm{1} \\[1.1ex] 3 & -2 & \color{red}\bm{0} \\[1.1ex] 1 & 3 & \color{red}\bm{5}\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-24}{24} = \bm{-1}$

したがって、連立方程式の解は次のようになります。

$\displaystyle \bm{x = 1 \qquad y=2 \qquad z = -1}$

例 2: 不確定互換システム (ICS)

クラマーの法則を使用して次の連立方程式を解きます。

$\begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \\[1.5ex] x+5y+3z = 1 \end{cases}$

まず、システムの行列 A と拡張行列 A’ を作成します。

$\displaystyle A= \left( \begin{array}{ccc} 3 & 2 & 4 \\[1.1ex] -2 & 3 & -1 \\[1.1ex] 1 & 5 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & 2 & 4 & 1 \\[1.1ex] -2 & 3 & -1 & 0 \\[1.1ex] 1 & 5 & 3 & 1 \end{array} \right)$

ここで 2 つの行列の範囲を計算し、それがどのようなタイプのシステムであるかを確認します。 A のランクを計算するには、行列全体の行列式を (Sarrus ルールを使用して) 計算し、それが 0 であるかどうかを確認します。

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & 2 & 4 \\[1.1ex] -2 & 3 & -1 \\[1.1ex] 1 & 5 & 3\end{vmatrix} = 27-2-40-12+15+12= 0$

行列式は 0 を与えるため、行列 A はランク 3 ではありません。しかし、行列式は 0 とは異なる 2×2 行列式を持ちます。

$\displaystyle \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3 \end{vmatrix} =9-(-4)=13\neq 0$

したがって、行列 A のランクは 2 です。

$\displaystyle rg(A)=2$

行列 A の範囲がわかったら、行列 A’ の範囲を計算します。最初の 3 列の行列式は 0 を与えるため、行列 A’ 内の他の可能な 3×3 行列式を試します。

$\displaystyle \begin{vmatrix} 2 & 4 & 1 \\[1.1ex] 3 & -1 & 0 \\[1.1ex] 5 & 3 & 1 \end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & 4 & 1 \\[1.1ex] -2 & -1 & 0 \\[1.1ex] 1 & 3 & 1 \end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & 2 & 1 \\[1.1ex] -2 & 3 & 0 \\[1.1ex] 1 & 5 & 1 \end{vmatrix} = 0$

次数 3 の行列式はすべて 0 になります。しかし、明らかに、行列 A’ には行列 A と同じ非 0 の 2×2 行列式があります。

$\displaystyle \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3 \end{vmatrix} =9-(-4)=13\neq 0$

したがって、行列 A’ もランク 2 になります。

$\displaystyle rg(A')=2$

したがって、行列 A のランクは行列 A’ のランクに等しいが、これら 2 つはシステム (3) の未知数の数より小さいため、ルーシェ-フロベニウスの定理によって、これは不定互換性のあるシステムであることがわかります。 (ICS):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}$

互換性のある不定系 (SCI) を解きたいときは、系を変換する必要があります。まず方程式を消去し、次に変数を λ (通常は変数 z) に変換し、最後に λ を含む項を次のようにまとめます。独立した用語。

システムを変換したら、Cramer の法則を適用して、システムの解を λ の関数として取得します。

この場合、システムから最後の方程式を削除します。

$\begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \\[1.5ex]\cancel{x+5y+3z = 1} \end{cases} \longrightarrow \quad \begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0\end{cases}$

次に、変数 z を λ に変換しましょう。

$\begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 3x+2y+4\lambda=1 \\[1.5ex] -2x+3y-\lambda=0\end{cases}$

そして、λ を含む項を独立した項に置きます。

$\begin{cases} 3x+2y=1-4\lambda \\[1.5ex] -2x+3y=\lambda \end{cases}$

したがって、システムの行列 A と行列 A’ は残ります。

$\displaystyle A= \left( \begin{array}{ccc} 3 & 2 \\[1.1ex] -2 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 3 & 2 & 1 -4\lambda \\[1.1ex] -2 & 3 & \lambda \end{array} \right)$

最後に、システムを変換したら、 Cramer のルールを適用します。したがって、A の行列式を解きます。

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3\end{vmatrix} = 13$

未知のものを計算するには

$\displaystyle x$

Cramer の規則を使用して、A の行列式の最初の列を独立項の列で変更し、それを A の行列式で割ります。

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 1 -4\lambda & 2 \\[1.1ex] \lambda & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3(1-4\lambda) -2\lambda}{13} = \cfrac{\bm{3-14\lambda} }{\bm{13}}$

未知のものを計算するには

$\displaystyle y$

Cramer の規則を使用して、A の行列式の 2 番目の列を独立項の列で変更し、それを A の行列式で割ります。

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 3 & 1 -4\lambda \\[1.1ex]-2& \lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3\lambda -\bigl(-2(1-4\lambda)\bigr)}{13}= \cfrac{3\lambda -\bigl(-2+8\lambda\bigr)}{13} = \cfrac{\bm{2-5\lambda} }{\bm{13}}$

連立方程式の解は λ の関数ですが、これは SCI であるため、無限に多くの解があります。

$\displaystyle \bm{x =} \cfrac{\bm{3-14\lambda} }{\bm{13}} \qquad \bm{y=}\cfrac{\bm{2-5\lambda} }{\bm{13}} \qquad \bm{z = \lambda}$

クレーマーの法則で問題が解決される

演習 1

Cramer の規則を適用して、2 つの未知数を含む次の 2 つの方程式系を解きます。

解決策を参照

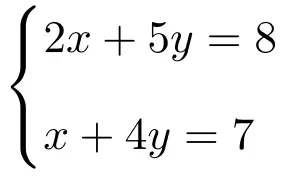
最初に行うことは、システムの行列 A と拡張行列 A’ です。

$\displaystyle A= \left( \begin{array}{cc} 2 & 5 \\[1.1ex] 1 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 2 & 5 & 8 \\[1.1ex] 1 & 4 & 7 \end{array}\right)$

次に、行列 A のランクを見つける必要があります。これを行うには、行列全体の行列式が 0 と異なるかどうかを確認します。

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 5 \\[1.1ex] 1 & 4 \end{vmatrix} = 8-5=3 \bm{\neq 0}$

行列には 0 とは異なる 2×2 行列式があるため、行列 A のランクは 2 になります。

$\displaystyle rg(A)=2$

A のランクがわかったら、A’ のランクを計算します。これは、内部に 0 とは異なる次数 2 の行列式があることがわかったばかりなので、少なくともランク 2 になります。さらに、3×3 の行列式を作成できないため、ランク 3 になることはできません。したがって、行列 A’ もランク 2 になります。

$\displaystyle rg(A')=2$

したがって、ルーシェ-フロベニウスの定理を適用すると、 A の範囲が A’ の範囲および未知数の数に等しいため、これが互換性のある決定系(SCD) であることがわかります。

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 2 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 2 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

システムが SCD であることがわかったら、それを解決するためにCramer の法則を適用します。

未知のものを計算するには

$\displaystyle x$

Cramer の規則を使用して、A の行列式の最初の列を独立項の列で変更し、それを A の行列式で割ります。

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 8 & 5 \\[1.1ex] 7 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-3}{3} = \bm{-1}$

未知のものを計算するには

$\displaystyle y$

Cramer の規則を使用して、A の行列式の 2 番目の列を独立項の列で変更し、それを A の行列式で割ります。

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}2 & 8 \\[1.1ex] 1 & 7\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{6}{3} = \bm{2}$

したがって、連立方程式の解は次のようになります。

$\displaystyle \bm{x = -1 \qquad y=2}$

演習 2

Cramer の法則を使用して、3 つの未知数を含む次の 3 つの方程式系の解を求めます。

解決策を参照

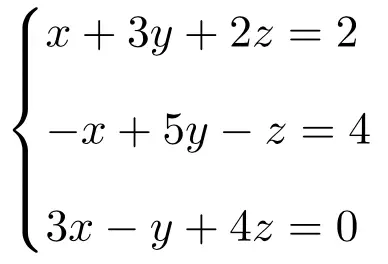
まず、システムの行列 A と拡張行列 A’ を作成します。

$\displaystyle A= \left( \begin{array}{ccc} 1 & 3 & 2\\[1.1ex] -1 & 5 & -1\\[1.1ex] 3 & -1 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 3 & 2 & 2 \\[1.1ex] -1 & 5 & -1 & 4 \\[1.1ex] 3 & -1 & 4 & 0 \end{array}\right)$

ここで、Sarrus ルールを使用して 3×3 行列の行列式を計算して、行列 A のランクを求めます。

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 3 & 2 \\[1.1ex] -1 & 5 & -1\\[1.1ex] 3 & -1 & 4 \end{vmatrix} = 20-9+2-30-1+12=-6 \bm{\neq 0}$

0 とは異なる次数 3 の行列式を持つ行列、行列 A はランク 3 です。

$\displaystyle rg(A)=3$

したがって、行列 A’ もランク 3 になります。

$\displaystyle rg(A')=3$

したがって、ルーシェ-フロベニウスの定理を使用すると、 A の範囲が A’ の範囲および未知数の数に等しいため、これが互換性のある決定系(SCD) であることがわかります。

システムが SCD であることがわかったら、システムを解くためにCramer の法則を適用する必要があります。

未知のものを計算するには

$\displaystyle x$

Cramer の規則を使用して、A の行列式の最初の列を独立項の列で変更し、それを A の行列式で割ります。

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2 & 3 & 2 \\[1.1ex] 4 & 5 & -1\\[1.1ex]0 & -1 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-18}{-6} = \bm{3}$

未知のものを計算するには

$\displaystyle y$

Cramer の規則を使用して、A の行列式の 2 番目の列を独立項の列で変更し、それを A の行列式で割ります。

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}1 & 2 & 2 \\[1.1ex] -1 & 4 & -1\\[1.1ex] 3 & 0 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-6}{-6} = \bm{1}$

計算する

$\displaystyle z$

Cramer の規則を使用して、A の行列式の 3 番目の列を独立項の列で変更し、それを A の行列式で割ります。

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} 1 & 3 & 2 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 3 & -1 & 0\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{12}{-6} = \bm{-2}$

したがって、連立方程式の解は次のようになります。

$\displaystyle \bm{x =3 \qquad y=1 \qquad z=-2}$

演習 3

Cramer の法則を使用して、3 つの未知数を含む次の 3 つの方程式系の解を計算します。

解決策を参照

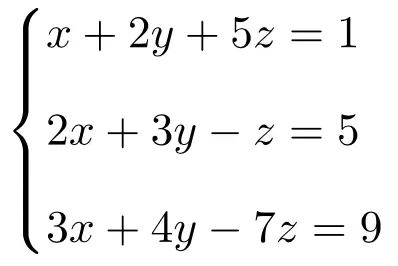
まず、システムの行列 A と拡張行列 A’ を作成します。

$\displaystyle A= \left( \begin{array}{ccc} 1 & 2 & 5\\[1.1ex] 2 & 3 & -1 \\[1.1ex] 3 & 4 & -7 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 2 & 5 & 1 \\[1.1ex] 2 & 3 & -1 & 5 \\[1.1ex] 3 & 4 & -7 & 9 \end{array}\right)$

行列 A の範囲を計算します。

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 2 & 5\\[1.1ex] 2 & 3 & -1 \\[1.1ex] 3 & 4 & -7 \end{vmatrix} =-21-6+40-45+4+28=0$

$\displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3 \end{vmatrix} = 3-4 = -1 \neq 0$

$\displaystyle rg(A)=2$

$\displaystyle \begin{vmatrix} 2 & 5 & 1 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 4 & -7 & 9 \end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 5 & 1 \\[1.1ex] 2 & -1 & 5 \\[1.1ex] 3 & -7 & 9\end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 2 & 1 \\[1.1ex] 2 & 3 & 5 \\[1.1ex] 3 & 4 & 9 \end{vmatrix} = 0$

次数 3 の行列式はすべて 0 になります。ただし、行列 A’ には行列 A と同じ 2×2 の非 0 行列式があります。

$\displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3 \end{vmatrix} = 3-4 = -1 \neq 0$

したがって、行列 A’ もランク 2 になります。

$\displaystyle rg(A')=2$

行列 A のランクは行列 A’ のランクと等しいですが、これら 2 つはシステム (3) の未知数の数より小さいため、ルーシェ-フロベニウスの定理によって、それが不確定互換システム(ICS) であることがわかります。

ICS システムであるため、方程式を削除する必要があります。この場合、システムから最後の方程式を削除します。

$\begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5 \\[1.5ex]\cancel{3x+4y-7z = 9} \end{cases} \longrightarrow \quad \begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5\end{cases}$

次に、変数 z を λ に変換しましょう。

$\begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} x+2y+5\lambda=1 \\[1.5ex] 2x+3y-\lambda=5\end{cases}$

そして、λ を含む項を独立した項に置きます。

$\begin{cases} x+2y=1-5\lambda\\[1.5ex] 2x+3y=5+\lambda \end{cases}$

システムの行列 A と行列 A’ はそのまま残ります。

$\displaystyle A= \left( \begin{array}{ccc} 1 & 2 \\[1.1ex] 2 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 1 & 2 & 1 -5\lambda \\[1.1ex] 2 & 3 &5+\lambda \end{array} \right)$

最後に、システムを変換したら、 Cramer のルールを適用します。したがって、A の行列式を解きます。

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3\end{vmatrix} =-1$

未知のものを計算するには

$\displaystyle x$

Cramer の規則を使用して、A の行列式の最初の列を独立項の列で変更し、それを A の行列式で割ります。

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 1-5\lambda & 2 \\[1.1ex] 5+\lambda & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3-15\lambda -(10+2\lambda)}{-1} = \cfrac{-7-17\lambda}{-1} = \bm{7+17\lambda}$

未知のものを計算するには

$\displaystyle y$

Cramer の規則を使用して、A の行列式の 2 番目の列を独立項の列で変更し、それを A の行列式で割ります。

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 1 & 1-5\lambda \\[1.1ex] 2 & 5+\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{5+\lambda -(2-10\lambda)}{-1}= \cfrac{3+11\lambda}{-1} = \bm{-3-11\lambda}$

連立方程式の解は λ の関数ですが、これは SCI であるため、無限に多くの解があります。

$\displaystyle \bm{x =7+17\lambda} \qquad \bm{y=-3-11\lambda} \qquad \bm{z = \lambda}$

演習 4

Cramer の法則を適用して、3 つの未知数を含む 3 つの方程式系に関する次の問題を解きます。

$\begin{cases} -2x+5y+z=8 \\[1.5ex] 6x+2y+4z=4 \\[1.5ex] 3x-2y+z = -2 \end{cases}$

解決策を参照

まず、システムの行列 A と拡張行列 A’ を構築します。

$\displaystyle A= \left( \begin{array}{ccc}-2 & 5 & 1 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & 1\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} -2 & 5 & 1 & 8 \\[1.1ex] 6 & 2 & 4 & 4 \\[1.1ex] 3 & -2 & 1 & -2 \end{array}\right)$

ここで、Sarrus の法則を使用して 3×3 行列の行列式を計算して、行列 A のランクを計算してみましょう。

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} -2 & 5 & 1 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & 1 \end{vmatrix} = -4+60-12-6-16-30=-8 \bm{\neq 0}$

0 とは異なる次数 3 の行列式を持つ行列、行列 A はランク 3 です。

$\displaystyle rg(A)=3$

したがって、行列 A’ もランク 3 になります。これは、行列 A と少なくとも同じランクでなければならず、次元 3×4 の行列であるためランク 4 にすることはできません。

$\displaystyle rg(A')=3$

したがって、ルーシェ-フロベニウスの定理を使用して、 A の範囲が A’ の範囲および未知数の数に等しいため、これが決定互換システム(SCD) であると推定します。

システムが SCD であることがわかったら、システムを解くためにCramer の法則を適用する必要があります。

未知のものを計算するには

$\displaystyle x$

Cramer の規則を使用して、A の行列式の最初の列を独立項の列で変更し、それを A の行列式で割ります。

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 8 & 5 & 1 \\[1.1ex] 4 & 2 & 4 \\[1.1ex] -2 & -2 & 1\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{16}{-8} = \bm{-2}$

未知のものを計算するには

$\displaystyle y$

Cramer の規則を使用して、A の行列式の 2 番目の列を独立項の列で変更し、それを A の行列式で割ります。

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}-2 & 8 & 1 \\[1.1ex] 6 & 4 & 4 \\[1.1ex] 3 & -2 & 1\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-6} = \bm{0}$

計算する

$\displaystyle z$

Cramer の規則を使用して、A の行列式の 3 番目の列を独立項の列で変更し、それを A の行列式で割ります。

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} -2 & 5 & 8 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & -2\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-32}{-8} = \bm{4}$

したがって、線形方程式系の解は次のようになります。

$\displaystyle \bm{x =-2 \qquad y=0 \qquad z=4}$

演習 5

クラマーの法則を使用して次の連立一次方程式を解きます。

解決策を参照

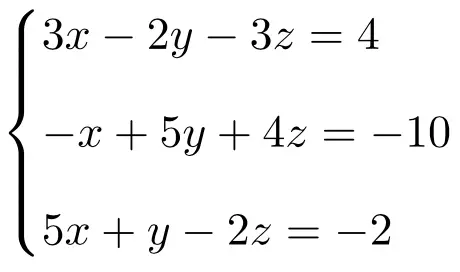
まず、システムの行列 A と拡張行列 A’ を作成します。

$\displaystyle A= \left( \begin{array}{ccc} 3 & -2 & -3 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 5 & 1 & -2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & -2 & -3 & 4 \\[1.1ex] -1 & 5 & 4 & -10 \\[1.1ex] 5 & 1 & -2 & -2 \end{array}\right)$

行列 A の範囲を計算します。

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & -2 & -3 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 5 & 1 & -2 \end{vmatrix} =-30-40+3+75-12+4=0$

$\displaystyle \begin{vmatrix} 3 & -2 \\[1.1ex] -1 & 5 \end{vmatrix} = 15- (2)= 13 \neq 0$

$\displaystyle rg(A)=2$

$\displaystyle \begin{vmatrix} -2 & -3 & 4 \\[1.1ex] 5 & 4 & -10 \\[1.1ex] 1 & -2 & -2 \end{vmatrix} = 0 \qquad \begin{vmatrix}3 & -3 & 4 \\[1.1ex] -1 & 4 & -10 \\[1.1ex] 5 & -2 & -2\end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & -2 & 4 \\[1.1ex] -1 & 5 & -10 \\[1.1ex] 5 & 1 &-2\end{vmatrix} = 0$

次数 3 の行列式はすべて 0 になります。しかし、明らかに、行列 A’ には行列 A と同じ 0 以外の次数 2 の行列式があります。

$\displaystyle \begin{vmatrix} 3 & -2 \\[1.1ex] -1 & 5 \end{vmatrix} = 13 \neq 0$

したがって、行列 A’ もランク 2 になります。

$\displaystyle rg(A')=2$

行列 A のランクは行列 A’ のランクに等しいですが、これら 2 つはシステムの未知数の数 (3) より小さいため、ルーシェ-フロベニウスの定理により、それが不確定システム互換(SCI) であることがわかります。 :

ICS システムであるため、1 つの方程式を削除する必要があります。この場合、システムから最後の方程式を削除します。

$\begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10 \\[1.5ex]\cancel{5x+y-2z = -2} \end{cases} \longrightarrow \quad \begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10\end{cases}$

次に、変数 z を λ に変換しましょう。

$\begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 3x-2y-3\lambda=4 \\[1.5ex] -x+5y+4\lambda=-10\end{cases}$

そして、λ を含む項を独立した項に置きます。

$\begin{cases} 3x-2y=4+3\lambda \\[1.5ex] -x+5y=-10-4\lambda\end{cases}$

システムの行列 A と行列 A’ はそのまま残ります。

$\displaystyle A= \left( \begin{array}{ccc} 3 & -2 \\[1.1ex] -1 & 5 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 3 & -2 & 4+3\lambda \\[1.1ex] 1 & 5 &-10-4\lambda \end{array} \right)$

最後に、システムを変換したら、 Cramer のルールを適用します。したがって、A の行列式を解きます。

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}3& -2 \\[1.1ex] -1 & 5\end{vmatrix} =13$

未知のものを計算するには

$\displaystyle x$

Cramer の規則を使用して、A の行列式の最初の列を独立項の列で変更し、それを A の行列式で割ります。

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 4+3\lambda & -2 \\[1.1ex]-10-4\lambda & 5\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{20+15\lambda -(20+8\lambda)}{13} = \cfrac{\bm{7\lambda}}{\bm{13}}$

未知のものを計算するには

$\displaystyle y$

Cramer の規則を使用して、A の行列式の 2 番目の列を独立項の列で変更し、それを A の行列式で割ります。

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 3 & 4+3\lambda \\[1.1ex] -1 & -10-4\lambda\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-30-12\lambda -(-4-3\lambda)}{13}= \cfrac{\bm{-26-9\lambda}}{\bm{13}}$

したがって、連立方程式の解は λ の関数です。これは SCI であるため、この系には無限に多くの解があります。

$\displaystyle \bm{x=} \cfrac{\bm{7\lambda}}{\bm{13}} \qquad \bm{y=} \cfrac{\bm{-26-9\lambda}}{\bm{13}} \qquad \bm{z = \lambda}$

クラマーの法則とは何ですか?

例 1: 決定された互換性のあるシステム (SCD)

例 2: 不確定互換システム (ICS)

クレーマーの法則で問題が解決される

演習 1

演習 2

演習 3

演習 4

演習 5

コメントする 返信をキャンセル

コメントする返信をキャンセル