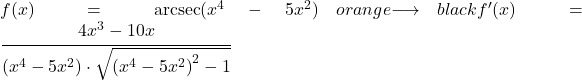このページでは、アークセカントの導関数 (公式) が何かを説明します。関数のアークセカントの導関数に関する解決済みの演習が見つかります。
アークセカントの微分公式
x の逆正割の導関数は、x の積に x の 2 乗根を掛けて 1 を引いたものです。
![]()
したがって、関数の逆正割の微分値は、その関数の微分値を関数で割った商に、その関数の平方根を掛けてから 1 を引いた値に等しくなります。
![]()
明らかに、2 番目の式は最初の式に似ていますが、2 つの唯一の違いは、2 番目の式では連鎖規則が適用されることです。

逆関数なので奇妙に思えるかもしれませんが、逆正割の導関数は正割の導関数とは何の関係もありません。ここをクリックすると、セカントの導関数の公式を確認できます。
➤ 「セカントの導関数」を参照
逆正割導関数の例
例1
この例では、一次関数 7x の逆正割の導関数がどのくらいであるかを確認します。
![]()
アークセカントの導関数を求めるには、次のような対応する式を適用する必要があります。
![]()
7x 関数の導関数は 7 であるため、7x 関数のアークセカントの導関数は次のようになります。
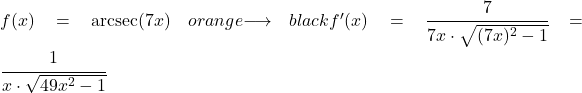
例 2
この 2 番目の例では、ポテンシャル関数のアークセカントを導出します。
![]()
逆正割関数の引数に x 以外の項があるため、関数全体を導出するには逆正割微分規則と連鎖規則を適用する必要があります。
![]()
したがって、分子に関数の引数の導関数を書き、分母にポテンシャル関数を書き直して、引数の関数の 2 マイナス 1 乗の平方根を掛けます。