べき乗（またはポテンシャル関数）の導関数

9月 17, 2023

ここでは、べき乗 (またはポテンシャル関数) を導出する方法を説明し、べき乗の導関数の公式といくつかの例を示し、ステップごとに解いた演習で練習することもできます。

べき乗の導関数の公式

べき乗の導関数、またはポテンシャル関数は、べき乗の指数と底の累乗値から底の導関数の 1 倍を引いた積です。

$f(x)=u^k \quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=k\cdot u^{k-1}\cdot u'$

したがって、底が恒等関数の場合、累乗を求めるには、単純に関数に指数を乗算し、指数から 1 単位を減算します。

$f(x)=x^k \quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=k\cdot x^{k-1}$

実際、恒等関数の導関数は 1 に等しくなります。

要約すると、ポテンシャル関数を導出するには 2 つの公式があります。1 つ目は常に使用でき、2 つ目は基数が x の場合にのみ適用できます。

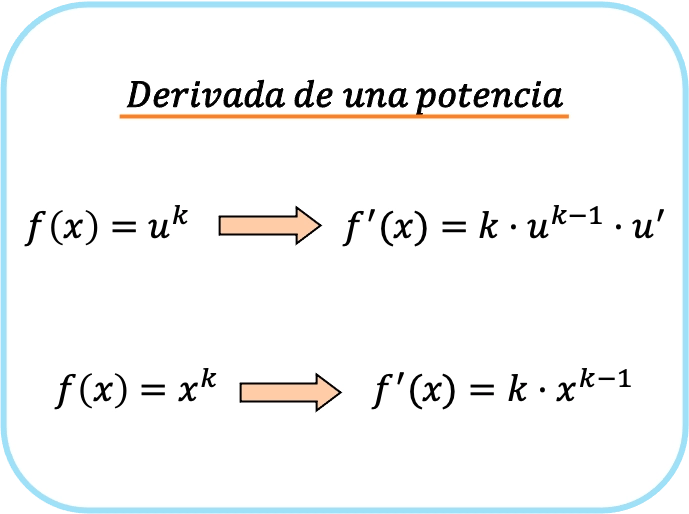
力から派生した

べき乗の導関数として提示された最初の式が 2 番目の式と似ていますが、連鎖則が適用されていることを簡単に検証できます。

これらの式は、変数がべき乗の底である場合にのみ使用できることに注意してください。x が分母にある場合は、指数関数の導関数のルールを適用する必要があります。

➤参照: 指数関数の導関数

電力デリバティブの例

ポテンシャル関数の導関数の公式を理解したら、べき乗がどのように導出されるかを理解できるように、このタイプの導関数の例をいくつか説明します。

例 1: 基準電力 x の導関数

$f(x)=x^4$

前のセクションで説明したように、べき乗の底が x のみの場合、関数を導出するために使用する必要がある公式は次のとおりです。

$f(x)=x^k \quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=k\cdot x^{k-1}$

したがって、x の 4 乗の導関数は次のようになります。

$f(x)=x^4 \quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=4\cdot x^{4-1}=4x^3$

例 2: 括弧付きのべき乗の導関数

$f(x)=(2x-1)^5$

この例では、基数は恒等関数ではないため、べき乗の導関数には一般式を使用する必要があります。

$f(x)=u^k \quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=k\cdot u^{k-1}\cdot u'$

括弧内の関数は線形関数であるため、その導関数は 2 です。したがって、ポテンシャル関数全体の導関数は次のようになります。

$f(x)=(2x-1)^5 \quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=5\cdot (2x-1)^4\cdot 2=10(2x-1)^4$

例 3: 負のべき乗の導関数

$f(x)=(\log 9x)^{-2}$

この場合、指数が負で底が対数であるポテンシャル関数があるため、次の式を使用して関数を微分します。

$f(x)=u^k \quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=k\cdot u^{k-1}\cdot u'$

べき指数が負の場合でも、そこから 1 を減算する必要があります。したがって、関数の導関数は次のようになります。

$f'(x)=-2\cdot (\log 9x)^{-3}\cdot \cfrac{1}{9x\cdot \ln 10}\cdot 9 =\cfrac{-2(\log 9x)^{-3}}{x\ln 10}$

解決策について疑問がある場合は、ここで対数関数の導関数の公式を参照してください。

➤参照: 対数関数の導関数

例 4: ルートを使用した累乗の導関数

$f(x)=\sqrt[3]{(5x+2)^7}$

この例の関数は、正規表現内の累乗です。ただし、根号はポテンシャル式に変換できるため、小数指数を含むポテンシャル関数に変換することで関数を簡略化できます。

$f(x)=(5x+2)^{\frac{7}{3}}$

ここで、変数の累乗の導関数の公式を適用します。

$f(x)=u^k \quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=k\cdot u^{k-1}\cdot u'$

そして導関数は次のとおりです。

$f'(x)=\cfrac{7}{3}\cdot (5x+2)^{\frac{7}{3}-1} \cdot 5=\cfrac{35}{3}(5x+2)^{\frac{4}{3}}$

ルート導関数ルールを使用して、これらのタイプの関数を区別することもできます。

➤参照: ルートからの派生

べき乗の微分に関する演習を解決しました

次の累乗の導関数を計算します。

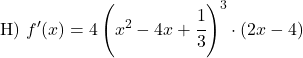
$\text{A) } f(x)=x^8$

$\text{B) } f(x)=3x^5$

$\text{C) } f(x)=-2x^{-4}$

$\text{D) } f(x)=(3x^2-4x)^6$

$\text{E) } f(x)=6(x^2+10)^3$

$\text{F) } f(x)=\cfrac{1}{(9x+2)^3}$

$\text{G) } f(x)=\sqrt{4x^5}$

$\text{H) } \displaystyle f(x)=\left(x^2-4x+\frac{1}{3}\right)^4$

$\text{I) } f(x)=\text{sen}^3(6-2x)$

解決策を見る

$\text{A) } f'(x)=8x^7$

$\text{B) } f'(x)=15x^4$

$\text{C) } f'(x)=8x^{-5}$

$\text{D) } f'(x)=6(3x^2-4x)^5\cdot (3x-4)$

$\text{E) } f'(x)=3\cdot 6(x^2+10)^2 \cdot 2x=36x(x^2+10)^2$

$\text{F) } f'(x)=-3\cdot (9x+2)^{-4}\cdot 9 =-27(9x+2)^{-4}$

$\text{G) } f'(x)=\cfrac{5}{2}\cdot 2x^{\frac{5}{2}-1} =5x^{\frac{3}{2}}$

$\text{H) } \displaystyle f'(x)=4\left(x^2-4x+\cfrac{1}{3}\right)^3\cdot (2x-4)$

$\text{I) } f'(x)=3\text{sen}^2(6-2x)\cdot \text{cos}(6-2x)\cdot (-2)=-6x\cdot \text{sen}^2(6-2x)\cdot \text{cos}(6-2x)$

コメントする返信をキャンセル