この記事では関数でどのような操作ができるのかを解説します。関数を使った操作の解説と演習問題をご覧いただけます。最後に、関数を使用した操作のプロパティを確認します。
関数を使った操作とは何ですか?
関数では、加算、減算、積、除算、合成の 5 種類の演算を実行できます。つまり、2 つの関数を加算、減算、乗算、除算、合成することができます。
次に、それぞれの操作が機能でどのように行われるのか、それぞれの特徴を見ていきます。
関数の和
2 つの関数の合計 (または加算)の値は、各関数の値の合計に等しくなります。言い換えれば、合計関数のイメージを計算するには、演算に関係する関数のイメージを単純に加算するだけです。
![]()
さらに、2 つの関数の和の定義域は、合計された各関数の定義域の交差になります。
![]()
例を使用して 2 つの関数がどのように追加されるかを見てみましょう。
![]()
まず、次の 2 つの関数を追加します。
![]()
そして今、sum関数の定義域を見つけます。これを行うために、各関数の定義域を個別に計算します。
![]()
➤参照:関数の定義域を計算する方法
この場合、操作の結果として得られる関数の定義域は次のようになります。
![]()
関数を使用した各操作には、結果を完全に定義するためのドメインを伴う必要があります。
関数の引き算
2 つの関数の減算 (または差)のイメージは、演算に参加する各関数のイメージの減算です。
![]()
加算関数と同様に、2 つの関数の減算領域は、各関数の領域の共通部分に相当します。
![]()
したがって、独立変数 x の特定の値で関数が定義されていない場合、減算の結果として得られる関数も定義されません。
例を通して 2 つの関数がどのように減算されるかを見てみましょう。
![]()
まず 2 つの関数を減算します。
![]()
次に、減算関数の定義域を決定します。
![]()
![]()
主力製品
2 つの関数の積または (乗算)を計算するには、各関数の式を単純に乗算する必要があります。
![]()
一方、積関数の定義域は、各乗算関数の定義域の共通部分の集合です。
![]()
たとえば、次の 2 つの関数があるとします。
![]()
まず、次の 2 つの関数を使用して製品の操作を実行します。
![]()
そして最後に、操作の結果として得られる関数の定義域を見つけます。
![]()
![]()
機能の分散
2 つの関数の除算 (または商)の数値結果は、次の方程式に対応します。
![]()
ただし、2 つの関数の除算の定義域は、各関数の定義域の交点の集合から、除数として機能する関数をキャンセルするすべての x を引いたものになります。そうしないと、不確定性が生じるからです。
![]()
例として、次の関数を分割します。
![]()
関数の分布は次のようになります。
![]()
一方、各関数の定義域はすべての実数で個別に構成されます。
![]()
ただし、分数の分母にゼロは存在できないため、結果の関数の定義域では、分母 (x=3) を打ち消すすべての値を削除する必要があります。
![]()
機能構成
関数の合成は最も複雑な概念であるため、解決するのが最も難しい操作です。
関数の合成は、 2 つの関数の連続した適用で構成されます。代数的には、2 つの関数の合成は次のように表されます。
![]()
一方、関数の合成領域は、
![]()
関数の定義域内の x のすべての値のセットと同等です
![]()
のような
![]()
機能の領域に属します
![]()
![]()
たとえば、次の 2 つの関数があるとします。
![]()
複合関数を見つけるには
![]()
に続く
![]()
の式を置き換える必要があります
![]()
どこにあるのか
![]()
の表現で
![]()
![Rendered by QuickLaTeX.com \begin{aligned}(g\circ f)(x)&=g\Bigl(f(x)\Bigr)\\[2ex]&= g\Bigl(x^2+1\Bigr)\\[2ex]&=3(x^2+1)-4\\[2ex]&=3x^2+3-4\\[2ex]&=3x^2-1\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f48079d61cf80409fdbf6610b5724189_l3.png)
この場合、両方の関数の定義域は完全に実数で構成されているため、合成関数の定義域も実数で構成されます。
![]()
ご覧のとおり、関数の作成は理解するのが簡単な操作ではありません。したがって、次の関数合成の演習を行うことをお勧めします。
➤参照: 関数の構成に関する演習を解いてください
関数を使用した操作のプロパティ
関数を使用したすべての演算のうち、和と積は次の特性によって特徴付けられます。
- 結合プロパティ: 3 つ以上の関数の加算または乗算の順序は関係ありません。
![]()
![]()
- 可換性の性質: 2 つの関数の加算または乗算の順序は結果を変更しません。
![]()
![]()
- 中立要素:和演算と積演算には一定の中立要素関数があります。
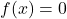
そして
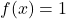
それぞれ。
- 対称要素: 和関数は逆の関数を持つ
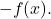
- 分配プロパティ: このプロパティは演算の合計と積を結び付け、次の等式に基づいています。
![]()