この関数を構成するさまざまな変数間の関係をグラフィカルに分析できるように関数を表現することは非常に一般的です。あるいは、このようなタイプの表現が複数の機能を購入するために使用されることもあります。これは、統計調査を実行する場合に特に使用されます。そうは言っても、今日は、たった 3 つのステップで任意の関数をグラフ化できる非常に簡単な方法を説明します。さらに、結論を導くためにグラフ結果を分析する方法についても説明します。
機能の種類
まず、さまざまなタイプの関数の特性と、それらを表すときにどのような違いを考慮する必要があるかを理解する必要があります。このようにすると、グラフ表示が容易になるため、各タイプについて簡単に説明します。関数には多くの種類があることに注意してください。ここでは、多項式関数と区分関数の 2 つの最も重要な種類に焦点を当てます。
一次関数
1 次の線形関数または多項式関数は、式が 1 次の多項式である関数です。その式はモデルf(x) = mx + nに従います。ここで、m は傾き、n は縦座標です。基本的に、これらの関数は線に相当するグラフィック形式を持ちます。以下に例を示します。
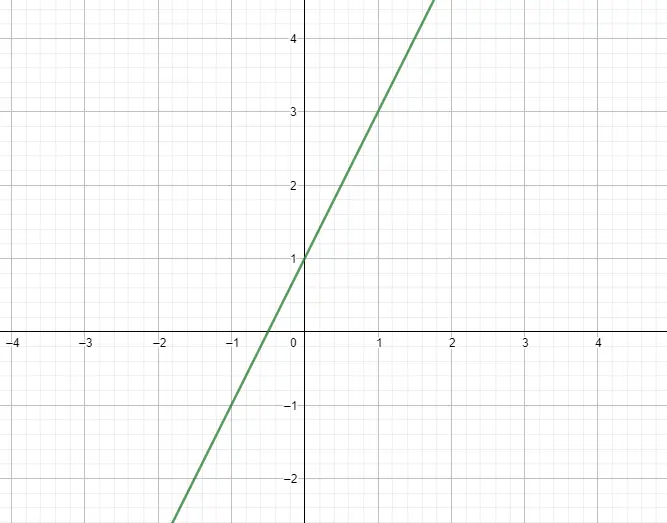
二次関数
二次関数または放物線関数は 2 次多項式を使用して表現されるため、放物線の形になります。従うべきモデルとして、次の式を考慮します: f(x) = ax² + bx + c、ここで a ≠ 0。また、これらの関数には他に 2 つの注目すべき特性、振幅と増加があります。以下に例を示します。
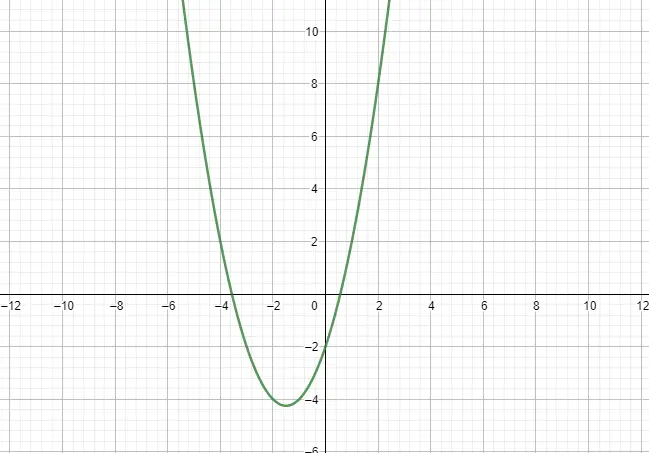
区分関数
区分的に定義された関数は、x の値に応じて異なる定義を持つ関数です。したがって、x が特定の値の範囲を占める場合は、式を試す必要があります。一方、x が他の値を占める場合は、別の式を処理する必要があります。ここに不連続性、つまり限界が見出されます。なぜなら、1 つの機能が終了しても、直接接続することなく別の機能を開始できるからです。以下に例を示します。
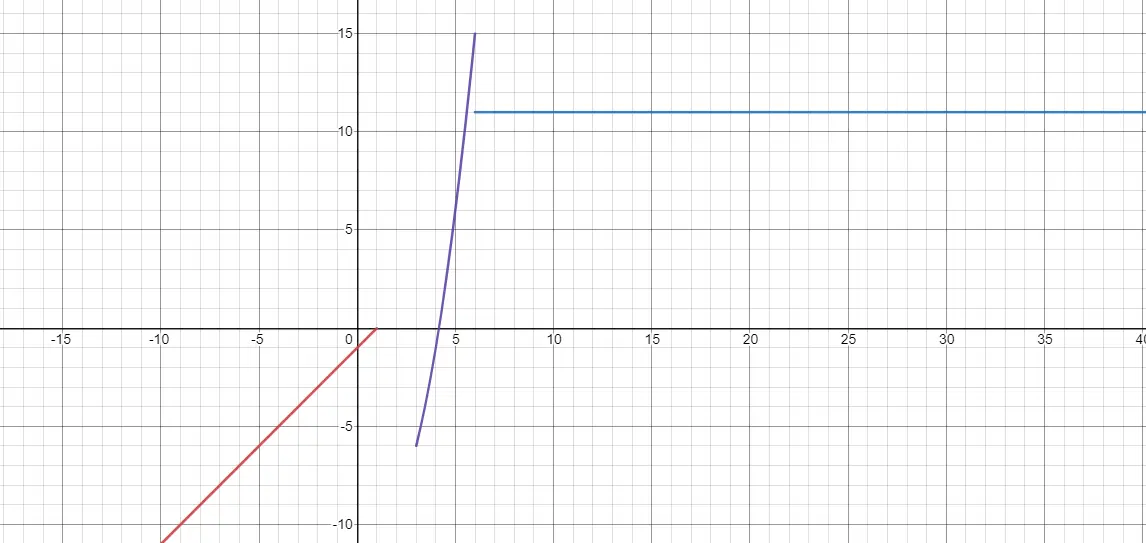
一次関数はどうやって表現するのでしょうか?
一次関数をグラフ化するには、3 つの非常に簡単な手順に従う必要があります。次に手順を説明しますが、放物線関数をグラフ化する方法を学びたい場合は、次のセクションを参照することをお勧めします。
値の表を作成する
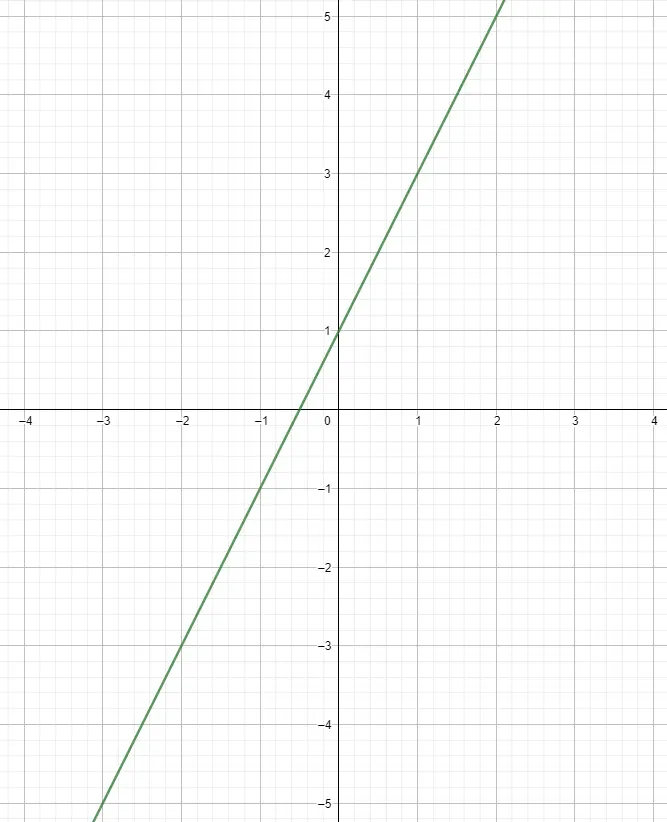
関数をグラフ化できるようにするには、変数のすべての値を書き込む値のテーブルを作成する必要があります。基本的に、これにより 2 つの変数間の関係を確立でき、この方法で関数のパスを追跡できます。値の表の作成方法がわからない場合は、この最後のリンクを参照してください。要約すると、独立変数に値を与え、それらに関連する関数に未知の値を代入することで構成されます。したがって、2 つの関連付けられた数値が得られます。次の表に例を示します。
関数 f(x) = 2x+1 より:
| バツ | f(x) |
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
グラフ上に点を描き、関数を描いてそれらを結合します
表を作成したら、グラフ上に点を描画し始めることができます。これを行うには、独立変数を x 軸に関連付け、もう一方を y 軸に関連付けます。このようにして点を取得します。好きなだけポイントを描画できますが、このスタイルの関数を表すには通常 5 つのポイントを計算するだけで十分です。それ以来、彼らはまっすぐな道を歩んできたので、どこまで進んでも同じです。
傾きを使用して一次関数をグラフ化する
値のテーブルを使用せずに線形関数をグラフィカルに表現できる 2 番目の方法は、関数の傾きを計算することで構成されます: m = (垂直方向の変化 / 水平方向の変化)。したがって、傾きを計算したら、開始点を確認する必要があります。前の例 f(x) = 2x+1 に戻ると、x = 0 ではコンピューター = 1 であるため、開始点は (0, 1) になることがわかります (式の +1 から推測します)。 。次に、傾きを追加するだけです。この場合、傾きは 1 水平に対して +2 垂直に等しくなります。すると次の点は(1,3)になることがわかります。
二次関数はどうやって表現するのでしょうか?
二次関数を表すには 2 つの方法に従うことができます。1 つ目は値のテーブルを使用します。 2 つ目は、一連のキーポイント (頂点、X 軸との交点、Y 軸との交点) を計算することで構成されます。後者については以下で説明します。
放物線の頂点を計算する
放物線関数の頂点を計算できる公式は 2 つあり、基本的に 1 つは X 軸の頂点を与え、もう 1 つは Y 軸の頂点を与えます。以下に両方の式を示しますが、どちらも同様の構造をしています。
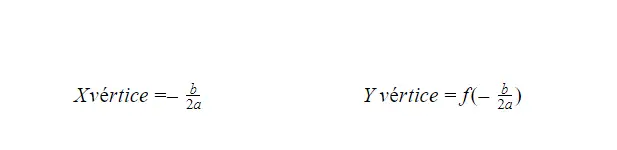
2次関数のX軸との交点を計算します。
の交点を取得するには、方程式を解くだけで済み、探している X の値がすでに得られています。二次関数であるため、1 つだけではなく 2 つの結果が得られることに注意してください。
2次関数のY軸との交点を計算します
最後に、Y 軸との交点を取得するには、単純に c = f(0) を計算します。そして、x = 0 のとき、放物線は常に垂直軸 (縦軸) と交差するため、Y 軸の切断点は (0,c) になると言えます。これらの点をすべて取得したら、それらをグラフ上に描画し、次のように放物線を描いてそれらを結合するだけです。
関数を区分的に表現するにはどうすればよいでしょうか?
関数を部分的に表現できるようにするには、これまでに説明したすべての方法を組み合わせることができます。このスタイルの関数は、これまで説明したすべての種類の関数で構成されているためです。したがって、値の表を通じて計算する必要があるものと、他の方法で計算する必要があるものがあります。ただし、この記事で説明したことをマスターすれば、関数を分割して表現するときに問題はなくなります。
一方、制限を表す場合は連続性の検討を行う必要があるため、 制限の解決方法がまだわからない場合は、その方法を学ぶことをお勧めします。これは、各関数のエンドポイントを正確に表すのに役立ちます。そうは言っても、これで区分関数やその他のタイプの関数をグラフ化する準備が整いました。ここで、一連のグラフ作成のヒントと、グラフを作成する電卓の機能についての非常に役立つ説明を残しておきます。
電卓でグラフを作成するにはどうすればよいですか?
グラフ電卓をお持ちの場合は、グラフを作成する機能があります。手順がわかれば非常に簡単に行えますが、まだやり方がわからない場合は、ここで説明します。
- グラフィックス モードにアクセスする:最初のステップは、メニューからグラフィックスまたはグラフィック表現のオプションにアクセスすることです。このオプションには、お使いの電卓とは異なる名前が付けられている場合がありますが、グラフやすでに説明したものに似た単語が含まれています。
- グラフ オプションをカスタマイズします。グラフ エディターに入ったら、ファイルに名前を付け、軸にラベルを付け、グラフ化する要素の数を選択し、表現の美的オプションを構成する必要があります。これは非常に簡単な手順です。
- 関数の点を追加します。その後、図形を形成する点の追加を開始できます。これを行うには、(0,1)、(3,2)… という表記で点を書きます。そして、グラフ化が完了するまで点を追加し続けます。
- 「プレビュー」機能を使用します。プロジェクトが完了したら、結果をプレビューして、期待どおりになるかどうかを確認できます。さらに、多くのテンプレートにはこのプレビューによる編集オプションがあるため、完璧になるまで結果を微調整できます。
- プロジェクトを保存する:編集手順全体が完了したら、覚えやすい場所にプロジェクトを保存してください。こうすることで、必要なときにいつでもプロジェクトに再度アクセスして、プロジェクトを表示したり、必要な改善を加えたりすることができます。
関数を表すのに最適な電卓
同じ電卓で関数を表現できるグラフィックス モデルの購入に興味がある場合は、 HP 50GとHP Primeの 2 つのモデルをお勧めします。これら 2 つは最高品質のモデルですが、高価であるため、投資に見合う価値があるかどうかを自問する必要があります。たとえば、数学に関して非常に複雑なエンジニアリングなどのキャリアを勉強する場合は、これら 2 つのモデルのいずれかを購入することを強くお勧めします。ただし、それほど多くのコンピューティング能力やグラフィックス能力を必要としない場合は、おそらくCasio FX-9750GIIで十分でしょう。
オンラインで関数をグラフ化するにはどうすればよいですか?
Desmos 、 Geogebraなどのオンライン グラフィックス プログラムを使用するオプションをいつでも選択できます。こうすることで、非常に正確なグラフを迅速に取得できます。数値形式は、関数を簡単かつ迅速にグラフ化したい場合に使用されると言えます。一方、関数をグラフ化して編集 (すべての属性を変更) でき、高品質の関数分析リソースをすぐに利用できるようにしたい場合は、関数電卓を購入することをお勧めします。