このページでは、逆行列とは何か、また行列式 (または随伴行列) の方法とガウス法によって逆行列を計算する方法を学びます。逆行列のすべてのプロパティも表示され、完全に理解できるように各メソッドの段階的な解決例と演習も表示されます。最後に、2×2 行列を素早く反転するための公式と、この行列演算の最大の用途である連立一次方程式を解くことについても説明します。
逆行列とは何ですか?
なれ
![]()
正方行列。の逆行列
![]()
それは書いてあります
![]()
、そしてそれはこの行列です:
![]()
![]()
金
![]()
は恒等行列です。
逆行列ができるのはどんなときで、できないのはどんなときでしょうか?
行列の可逆性を判断する最も簡単な方法は、行列式を使用することです。
- 問題の行列の行列式が 0 と異なる場合、これは行列が可逆であることを意味します。この場合、それは正則行列であると言えます。さらに、これは行列が最大ランクであることを意味します。
- 一方、行列の行列式が 0 に等しい場合、行列は反転できません。そしてこの場合、それは特異行列または縮退行列であると言います。
行列を反転するには主に 2 つの方法があります。行列式または随伴行列の方法とガウス方法です。以下に最初の説明がありますが、ガウス法を使用して行列を逆行列にする方法も以下で参照できます。
行列式を使用して (または隣接する行列を使用して) 行列を反転します。
逆行列を計算するには、
![]()
、次の式を適用する必要があります。
![]()
金:
-
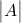
行列の行列式です

-
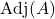
の随伴行列です

- 出展者
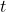
行列の転置を示します。つまり、添付された行列を転置する必要があります。
コメント:一部の書籍では、少し異なる逆行列公式を使用しています。最初に随伴行列を計算してから転置するのではなく、まず行列 A を転置してからその随伴行列を計算します。実際には、結果はまったく同じであるため、順序は重要ではありません。これを使用したい場合に備えて、変更された行列を反転するための式をここに残しておきます。

次に、例として演習を解いて逆行列を見つける方法を見ていきます。
行列式法 (または随伴行列) を使用して逆行列を計算する例:
- 次の行列の逆行列を計算します。
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 4 & -2 \\[1.1ex] 3 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c37ec4a7afd5b313bcf3c50d6ce26c6d_l3.png)
逆行列を決定するには、次の公式を適用する必要があります。
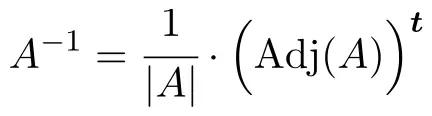
しかし、行列の行列式がゼロの場合、これは行列が可逆ではないことを意味します。したがって、最初に行うことは、行列の行列式を計算し、それが 0 と異なるかどうかを確認することです。
![Rendered by QuickLaTeX.com \displaystyle \lvert A \rvert = \begin{vmatrix} 4 & -2 \\[1.1ex] 3 & -1 \end{vmatrix} = -4- (-6) = 2](https://mathority.org/wp-content/ql-cache/quicklatex.com-710ccd4e4912dd492b496a742eaf7f56_l3.png)
行列式は 0 ではないため、行列は可逆です。
したがって、行列式の値を式に代入すると、行列の逆行列は次のようになります。
![]()
![]()
次に、A の代理行列を計算する必要があります。これを行うには、行列 A の各要素をその代理行列に置き換える必要があります。
の添付ファイルを計算するには、次のことを覚えておいてください。
![]()
、つまり行要素のことです
![]()
そしてコラム
![]()
、次の式を適用する必要があります。
![]()
ここで、
![]()
行を削除する行列の行列式です
![]()
そしてコラム
![]()
。
したがって、行列 A の要素の代理は次のようになります。
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 4 & -2 \\[1.1ex] 3 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c37ec4a7afd5b313bcf3c50d6ce26c6d_l3.png)
![]()
![]()
![]()
![]()
コメント:行列式 1×1 では数値が正に変換されないため、行列式 1×1 と絶対値を混同しないでください。
代理が計算されたら、単に A の要素をその代理で置き換えて、 A の代理行列を見つけます。
![Rendered by QuickLaTeX.com \displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} -1 & -3 \\[1.1ex] 2 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-08fb7666b4518399c2a469ba445762be_l3.png)
コメント:特定の場所では、随伴行列はここで定義する随伴行列の転置です。
したがって、添付の行列を逆行列の式に代入すると、次のようになります。
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{2} \cdot \begin{pmatrix} -1 & -3 \\[1.1ex] 2 & 4 \end{pmatrix} ^{\bm{t}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0abb4127db9c3c1d0a7b669fbc782605_l3.png)
出展者
![]()
これは、行列を転置する必要があることを示しています。そして、行列を転置するには、その行を 列 に変更する必要があります。つまり、行列の最初の行が行列の最初の列になり、2 番目の行が 2 番目の列になります。
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{2} \cdot \begin{pmatrix} -1 & 2 \\[1.1ex] -3 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-22965912cf8aee99610c81cf575c0ecd_l3.png)
最後に、行列の各項に次の値を掛けます。
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \sfrac{-1}{2} & \sfrac{2}{2} \\[1.1ex] \sfrac{-3}{2} & \sfrac{4}{2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-220748840151b429919c7ce6587b1bc0_l3.png)
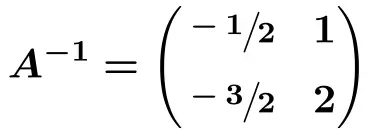
行列式の方法を使用した逆行列 (または隣接行列) に関する演習を解決しました。
演習 1
随伴行列法を使用して、次の次元 2×2 の行列を反転します。
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 7 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bfb0807249e78845b375a402eb23a32b_l3.png)
逆行列の式は次のとおりです。
![]()
まず行列の行列式を計算します。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A\end{vmatrix}=\begin{vmatrix} 1 & 3 \\[1.1ex] 2 & 7 \end{vmatrix} = 7-6 = 1](https://mathority.org/wp-content/ql-cache/quicklatex.com-1c4e3bac90eb0da0361b4be1a2225146_l3.png)
行列式は 0 とは異なるため、行列は反転できます。
ここで、A の随伴行列を計算してみましょう。
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} 7 & -2 \\[1.1ex] -3 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3dea8fca2c025ff9b7d7673904344996_l3.png)
行列の行列式とその随伴式が計算されたら、それらの値を式に代入します。
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{1} \cdot \begin{pmatrix} 7 & -2 \\[1.1ex] -3 & 1 \end{pmatrix}^{\bm{t}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9475e4162eff7e1ed9c08f363a8279ec_l3.png)
添付された行列を転置します。
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = 1 \cdot \begin{pmatrix} 7 & -3 \\[1.1ex] -2 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a5a6aaa8168e55c6eab1e3be1229a3da_l3.png)
したがって、A の逆行列は次のようになります。
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =} \begin{pmatrix} \bm{7} & \bm{-3} \\[1.1ex] \bm{-2} & \bm{1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1236ad7262705dbbd9b0a094084ceac5_l3.png)
演習 2
行列式法を使用して、次の正方行列を逆行列にします。
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} -3 & -2 \\[1.1ex] 5 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-eb735917d200ed35918cd44be6bd155b_l3.png)
逆行列の式は次のとおりです。
![]()
まず行列の行列式を計算します。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A\end{vmatrix}=\begin{vmatrix} -3 & -2 \\[1.1ex] 5 & 4\end{vmatrix} = -12+10 = -2](https://mathority.org/wp-content/ql-cache/quicklatex.com-49cd3daf7c50c811e78c29efe036bda4_l3.png)
行列式は 0 とは異なるため、行列は反転できます。
ここで、A の随伴行列を計算してみましょう。
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} 4 & -5 \\[1.1ex] 2 & -3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-208ab7161076485ca6928bd1208f6714_l3.png)
行列の行列式とその随伴式が見つかったら、それらの値を式に代入します。
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{-2} \cdot \begin{pmatrix} 4 & -5 \\[1.1ex] 2 & -3 \end{pmatrix}^{\bm{t}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-babecc87455bdc54006a77ba5369e540_l3.png)
添付された行列を転置します。
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{-2} \cdot \begin{pmatrix} 4 & 2 \\[1.1ex] -5 & -3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-17529597656a112a27d136ca212834d8_l3.png)
各要素に次の値を掛けます。
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \cfrac{4}{-2} & \cfrac{2}{-2} \\[3ex] \cfrac{-5}{-2} & \cfrac{-3}{-2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-be52d2df839244cbb0b0ee00c9e45265_l3.png)
したがって、A の逆行列は次のようになります。
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =} \begin{pmatrix} \bm{-2} & \bm{-1} \\[2ex] \cfrac{\bm{5}}{\bm{2}} & \cfrac{\bm{3}}{\bm{2}} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-13e218c7d075daba3f875345f324d001_l3.png)
演習 3
随伴行列法を使用して、次の次元 3×3 の行列を反転します。
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}2&3&-2\\[1.1ex] 1&4&1\\[1.1ex] 2&1&-3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d1b6a5f638281754d80983b5a50e15be_l3.png)
逆行列の式は次のとおりです。
![]()
まず、Sarrus ルールを使用して行列の行列式を解きます。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A\end{vmatrix}=\begin{vmatrix} 2&3&-2\\[1.1ex] 1&4&1\\[1.1ex] 2&1&-3 \end{vmatrix} = -24+6-2+16-2+9 = 3](https://mathority.org/wp-content/ql-cache/quicklatex.com-fcac1cb3935b1000b6493a2866e8728a_l3.png)
行列式は 0 とは異なるため、行列は反転できます。
行列式が解けたら、A の随伴行列が見つかります。
![Rendered by QuickLaTeX.com \text{Adjunto de 2} = \displaystyle (-1)^{1+1} \bm{\cdot} \begin{vmatrix} 4&1\\[1.1ex] 1&-3 \end{vmatrix} = 1 \cdot (-13) = \bm{-13}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c510482ac77a8c5d511c095de600f1ba_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 3} = \displaystyle (-1)^{1+2} \bm{\cdot} \begin{vmatrix}1&1\\[1.1ex] 2&-3\end{vmatrix} = -1 \cdot (-5) = \bm{5}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fa99e03d34c925098c1ad3ed6f06c745_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de -2} = \displaystyle (-1)^{1+3} \bm{\cdot} \begin{vmatrix} 1&4\\[1.1ex] 2&1 \end{vmatrix} = 1\cdot (-7) = \bm{-7}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3bf9f8565b3e4a99ff254c7558699c13_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 1} = \displaystyle (-1)^{2+1} \bm{\cdot} \begin{vmatrix} 3&-2 \\[1.1ex] 1&-3 \end{vmatrix} = -1 \cdot (-7) = \bm{7}](https://mathority.org/wp-content/ql-cache/quicklatex.com-99e2c3f55fbba7b5faa014758b60f4a8_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 4} = \displaystyle (-1)^{2+2} \bm{\cdot} \begin{vmatrix} 2&-2\\[1.1ex] 2&-3 \end{vmatrix} = 1 \cdot (-2) = \bm{-2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-23326bccecf752508e7418cbbc8eacd3_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 1} = \displaystyle (-1)^{2+3} \bm{\cdot} \begin{vmatrix} 2&3\\[1.1ex] 2&1\end{vmatrix} = -1 \cdot (-4) = \bm{4}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a9d056af07ce26751783152a67cdedb6_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 2} = \displaystyle (-1)^{3+1} \bm{\cdot} \begin{vmatrix} 3&-2\\[1.1ex] 4&1\end{vmatrix} = 1 \cdot 11 = \bm{11}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bed501806c35c94e491ad2063b2d0653_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 1} = \displaystyle (-1)^{3+2} \bm{\cdot} \begin{vmatrix} 2&-2\\[1.1ex] 1&1\end{vmatrix} = -1 \cdot 4 = \bm{-4}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3f108a61eec662b9420708f6920060be_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de -3} = \displaystyle (-1)^{3+3} \bm{\cdot} \begin{vmatrix} 2&3\\[1.1ex] 1&4 \end{vmatrix} = 1 \cdot 5 = \bm{5}](https://mathority.org/wp-content/ql-cache/quicklatex.com-77a152a00dbb5f1e0f8702dd9511095a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} -13 & 5 & -7 \\[1.1ex] 7 & -2 & 4 \\[1.1ex] 11 & -4 & 5 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b4642a75697fd30286065cdb4063a7bd_l3.png)
行列とその随伴物の行列式を計算したら、それらの値を式に代入します。
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{3} \cdot \begin{pmatrix} -13 & 5 & -7 \\[1.1ex] 7 & -2 & 4 \\[1.1ex] 11 & -4 & 5 \end{pmatrix}^{\bm{t}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fae003a07d40b69690566cde77857c3a_l3.png)
添付された行列を転置します。
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{3} \cdot \begin{pmatrix} -13 & 7 & 11 \\[1.1ex] 5 & -2 & -4 \\[1.1ex] -7 & 4 & 5 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-55717407766afe98f50ca75f20536edc_l3.png)
逆行列 A は次のようになります。
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =} \begin{pmatrix} \sfrac{\bm{-13}}{\bm{3}} & \sfrac{\bm{7}}{\bm{3}} & \sfrac{\bm{11}}{\bm{3}} \\[1.1ex] \sfrac{\bm{5}}{\bm{3}} & \sfrac{\bm{-2}}{\bm{3}} & \sfrac{\bm{-4}}{\bm{3}} \\[1.1ex] \sfrac{\bm{-7}}{\bm{3}} & \sfrac{\bm{4}}{\bm{3}} & \sfrac{\bm{5}}{\bm{3}}\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9835713a5b791ee959d6571d706180f3_l3.png)
演習 4
随伴行列法を使用して、次の 3 次行列を反転します。
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}4&5&-1\\[1.1ex] -1&3&2\\[1.1ex] 3&8&1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bf71320b51e9514d1c372389aeb3410a_l3.png)
逆行列の式は次のとおりです。
![]()
行列式が 0 の場合、行列には逆行列がないことを意味するため、最初に行列の行列式を計算する必要があります。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A\end{vmatrix}=\begin{vmatrix} 4&5&-1\\[1.1ex] -1&3&2\\[1.1ex] 3&8&1 \end{vmatrix} = 12+30+8+9-64+5 = \bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-eb7dc647f4121450eeadf2f5b62b4475_l3.png)
A の行列式は 0 であるため、行列を反転することはできません。
演習 5
次の 3 × 3 正方行列を行列式行列法で反転します。
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}1 & 4 & -3 \\[1.1ex] -2 & 1 & 0 \\[1.1ex] -1 & -2 & 2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-92e56e0f8013b6b65c0894a139537cae_l3.png)
逆行列の式は次のとおりです。
![]()
まず最初に、Sarrus ルールを使用して行列の行列式を解きます。
![Rendered by QuickLaTeX.com \displaystyle \lvert A \rvert = \begin{vmatrix} 1 & 4 & -3 \\[1.1ex] -2 & 1 & 0 \\[1.1ex] -1 & -2 & 2 \end{vmatrix} = 2+0-12-3-0+16 = 3](https://mathority.org/wp-content/ql-cache/quicklatex.com-07f116ed906c31644ed0513667988e6f_l3.png)
行列式は 0 とは異なるため、行列は反転できます。
行列式が解けたら、A の随伴行列が見つかります。
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de 1} = (-1)^{1+1} \bm{\cdot} \begin{vmatrix} 1 & 0 \\[1.1ex] -2 & 2 \end{vmatrix} = 1 \bm{\cdot} (2-0) = \bm{2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-20da2eac0d49b1134b39b1f5c95c5659_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de 4} = (-1)^{1+2} \bm{\cdot} \begin{vmatrix} -2 & 0 \\[1.1ex] -1 & 2 \end{vmatrix} = -1 \bm{\cdot} (-4-0) = \bm{4}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c5b80624f0963dfb1a111d96b4e1ceae_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de -3} = (-1)^{1+3} \bm{\cdot} \begin{vmatrix} -2 & 1 \\[1.1ex] -1 & -2 \end{vmatrix} = 1 \bm{\cdot} \bigl(4-(-1)\bigr) = \bm{5}](https://mathority.org/wp-content/ql-cache/quicklatex.com-50dd371e77d1896adb197321b68efd1d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de -2} = (-1)^{2+1} \bm{\cdot} \begin{vmatrix} 4 & -3 \\[1.1ex] -2 & 2 \end{vmatrix} = -1 \bm{\cdot} (8-6) = \bm{-2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-60b779f4366a3ef38ae522fcfca8e7d6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de 1} = (-1)^{2+2} \bm{\cdot} \begin{vmatrix} 1 & -3 \\[1.1ex] -1 & 2 \end{vmatrix} = 1 \bm{\cdot} (2-3) = \bm{-1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-51cb00c42e6932810a4220eb85c61acd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de 0} = (-1)^{2+3} \bm{\cdot} \begin{vmatrix} 1 & 4 \\[1.1ex] -1 & -2 \end{vmatrix} = -1 \bm{\cdot} \bigl(-2-(-4)\bigr) = \bm{-2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a3b26cbfa55d5567d2dae10c5dfbd158_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de -1} = (-1)^{3+1} \bm{\cdot} \begin{vmatrix} 4 & -3 \\[1.1ex] 1 & 0 \end{vmatrix} = 1 \bm{\cdot} \bigl(0-(-3)\bigr) = \bm{3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8d9f1bf4f5e01df910cd59bd4b25f816_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de -2} = (-1)^{3+2} \bm{\cdot} \begin{vmatrix} 1 & -3 \\[1.1ex] -2 & 0 \end{vmatrix} = -1 \cdot (0-6) = \bm{6}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8ce129b17734facf076e48fb1928d0e1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de 2} = (-1)^{3+3} \bm{\cdot} \begin{vmatrix} 1 & 4 \\[1.1ex] -2 & 1 \end{vmatrix} = 1 \bm{\cdot} \bigl(1-(-8)\bigr) = \bm{9}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3c8b319461dad7880bf2b9f20187b6fb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} 2 & 4 & 5 \\[1.1ex] -2 & -1 & -2 \\[1.1ex] 3 & 6 & 9 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-748fcb9d9d2a8326379da4d2bd08534a_l3.png)
行列とその随伴物の行列式を計算したら、それらの値を式に代入します。
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{3} \cdot \begin{pmatrix} 2 & 4 & 5 \\[1.1ex] -2 & -1 & -2 \\[1.1ex] 3 & 6 & 9\end{pmatrix}^{\bm{t}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3a0fc0e6effb520e22ff82c3034b4d4c_l3.png)
添付された行列を転置します。
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{3} \cdot \begin{pmatrix} 2 & -2 & 3 \\[1.1ex] 4 & -1 & 6 \\[1.1ex] 5 & -2 & 9 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bba6ddbc8ab9f2c64eb03cdb9fea530a_l3.png)
そして最後に、次の操作を行います。
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \sfrac{2}{3} & \sfrac{-2}{3} & \sfrac{3}{3} \\[1.1ex] \sfrac{4}{3} & \sfrac{-1}{3} & \sfrac{6}{3} \\[1.1ex] \sfrac{5}{3} & \sfrac{-2}{3} & \sfrac{9}{3} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-41f999c23e7d5ce129b410b9f486983e_l3.png)
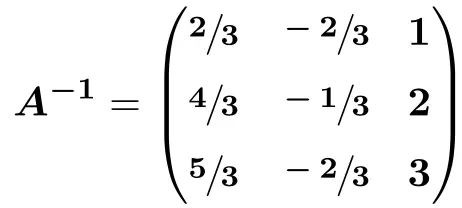
ガウス法を使用して行列を反転します。
ガウス法 を使用して行列の逆行列を計算するには、行列の行に対して演算を実行する必要があります(これについては後で説明します)。したがって、ガウス法の使用方法を説明する前に、行列の行に対して実行できるすべての演算を理解しておくことが重要です。
ガウス法で許可される線の変換
- 行列の行の順序を変更します。
たとえば、行列の 2 行目と 3 行目の順序を変更できます。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc} 3 & 5 & -2 \\[2ex] -2 & 4 & -1 \\[2ex] 6 & 1 & -3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{ f_2 \rightarrow f_3}} \\[2ex] \xrightarrow{ f_3 \rightarrow f_2}} \end{array} \left( \begin{array}{ccc} 3 & 5 & -2 \\[2ex] 6 & 1 & -3 \\[2ex] -2 & 4 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1d3f607625afb96bfb250168bd330818_l3.png)
- 行内のすべての項を 0 以外の数値で乗算または除算します。
たとえば、行 1 を 4 で乗算し、行 3 を 2 で割ることができます。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc} 1 & -2 & 3 \\[2ex] 3 & -1 & 5 \\[2ex] 2 & -4 & -2 \end{array} \right) \begin{array}{c} \xrightarrow{4 f_1} \\[2ex] \\[2ex] \xrightarrow{ f_3 / 2} \end{array} \left( \begin{array}{ccc} 4 & -8 & 12 \\[2ex] 3 & -1 & 5 \\[2ex] 1 & -2 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3cca4df71c23b1f005068a0a93b77dfe_l3.png)
- 行を、同じ行と別の行の合計に数値を乗算した値に置き換えます。
たとえば、次の行列では、行 3 に 1 を乗算した値を行 2 に追加します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc} -1 & -3 & 4 \\[2ex] 2 & 4 & 1 \\[2ex] 1 & -2 & 3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 1\cdot f_3} \\[2ex] & \end{array} \left( \begin{array}{ccc} -1 & -3 & 4 \\[2ex] 3 & 2 & 4 \\[2ex] 1 & -2 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8ca6644f015dd42ddbf4ab159bd10dec_l3.png)
ガウス法を使用した逆行列の計算例:
ガウス法を適用して行列を反転する方法を例で見てみましょう。
- 次の行列の逆行列を計算します。
![Rendered by QuickLaTeX.com \displaystyle A = \left( \begin{array}{ccc} 1 & 0 & 1 \\[2ex] 0 & 2 & 1 \\[2ex] 1 & 5 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-71553480cefa679dcb8eb98d97e0c717_l3.png)
最初に行う必要があるのは、 A 行列と恒等行列を 1 つの行列に結合することです。左側が A 行列、右側が恒等行列です。
![]()
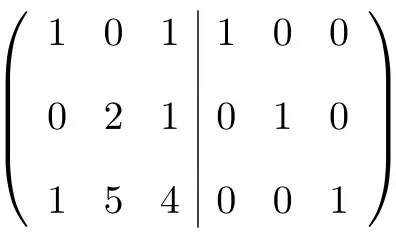
逆行列を計算するには、左行列を単位行列に変換する必要があります。そして、そのためには、そこに到達するまで行に変換を適用する必要があります。
列ごとに進みます。つまり、行に対して演算を実行して、最初に最初の列の数値を変換し、次に 2 列目の数値を変換し、最後に 3 列目の数値を変換します。
最初の列の 1 と 0 はすでに適切です。単位行列にもこれらの位置に 1 と 0 があるからです。したがって、現時点ではこれらの行に変換を適用する必要はありません。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} \color{blue}\boxed{\color{black}1} & 0 & 1 & 1 & 0 & 0 \\[2ex] \color{blue}\boxed{\color{black}0} & 2 & 1 & 0 & 1 & 0 \\[2ex] 1 & 5 & 4 &0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-7f51b3a869dde9c1697be9e57fce1548_l3.png)
ただし、単位行列の最初の列の最後の要素には 0 があり、現在は 1 になっています。したがって、1 を 0 に変換する必要があります。これを行うには、行 1 に – を乗算した値を行 3.1 に追加します。

したがって、この合計を実行すると、次の行列が得られます。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 2 & 1 & 0 & 1 & 0 \\[2ex] 1 & 5 & 4 &0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 - f_1} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 2 & 1 & 0 & 1 & 0 \\[2ex] \color{blue}\boxed{\color{black}0} & 5 & 3 & -1 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-992a31603c2182a97d31ddf787df4f06_l3.png)
こうして1を0に変えることに成功しました。
次に、左の行列の 2 列目に移ります。最初の要素は 0 ですが、単位行列の同じ位置に 0 があるため、これは適切です。ただし、2 の代わりに 1 が必要なので、2 行目を 2 で割ります。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 2 & 1 & 0 & 1 & 0 \\[2ex] 1 & 5 & 4 &0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2/2}\\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & \color{blue}\boxed{\color{black}1} & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 5 & 3 & -1 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a86b61ee601f9cd0ff9a70d1a280f887_l3.png)
さらに、2 列目でも 5 を 0 に変換する必要があります。5 は 2 行目の 1 の 5 倍であるため、行 2 に -5 を掛けた値を行 3 に追加します。

したがって、この操作を実行すると、2 列目の最後の要素に 0 が含まれる行列が得られます。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 5 & 3 & -1 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 - 5f_2} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & \color{blue}\boxed{\color{black}0} & \sfrac{1}{2} & -1 & \sfrac{-5}{2} & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-fcc790f05d73d308cb7d992841ab031a_l3.png)
最後に、行列の最後の列を左に変換しますが、今回は下から開始する必要があります。したがって、次のように変換する必要があります。
![]()
したがって、最後の行を 2 で乗算します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 0 & \sfrac{1}{2} & -1 & \sfrac{-5}{2} & 1 \end{array} \right)\begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{2f_3} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 0 & \color{blue}\boxed{\color{black}1} & -2 & -5 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-69614cae4dd388b6454ffd9b8d63c9a5_l3.png)
私たちは今、
![]()
ただし、今回は 1 を 2 に変換することになるため、行を 2 で乗算することはできません (単位行列のその位置に 1 がある場合)。したがって、行 3 を -2 で割ったものを行 2 に追加します。

したがって、この操作を実行することで、
![]()
0の場合:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 0 & 1 & -2 & -5 & 2 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2-f_3/2} \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \color{blue}\boxed{\color{black}0} & 1 & 3 & -1 \\[2ex] 0 & 0 & 1 & -2 & -5 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-537958a51f67c7602ef121fa2c997ca8_l3.png)
最後に、3 列目の最初の行の 1 を 0 に変換するだけです。 3 行目の同じ列にも 1 があるため、行 3 に -1 を掛けた値を行 1 に追加します。
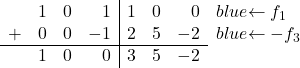
そして、この操作を行うことで、1 を 0 に変換することができます。
![Rendered by QuickLaTeX.com \ \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 &0 & 1 & 3 & -1 \\[2ex] 0 & 0 & 1 & -2 & -5 & 2 \end{array} \right) \begin{array}{c} \xrightarrow{f_1-f_3} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & \color{blue}\boxed{\color{black}0} & 3 & 5 & -2 \\[2ex] 0 & 1 & 0 & 1 & 3 & -1 \\[2ex] 0 & 0 & 1 & -2 & -5 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8ddd39df6bc92258ba163c65de4fd59f_l3.png)
左行列を恒等行列に変換できたら、逆行列もわかります。逆行列は、左側の行列を単位行列に変換して右側に得られる行列であるためです。したがって、行列の逆行列は次のようになります。
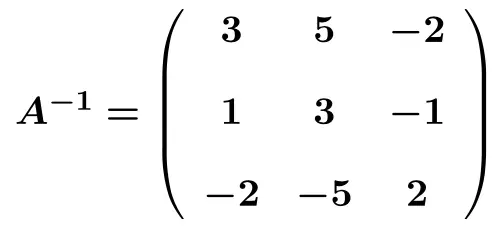
ガウス法を使用した逆行列の演習を解決しました。
演習 1
ガウス法を使用して次の行列を逆行列にします。
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & 2 \\[1.1ex] 1 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-36886e1ab1007f9a53bdc0dd71a0d15b_l3.png)
最初に行う必要があるのは、A 行列と恒等行列を 1 つの行列に結合することです。左側が A 行列、右側が単位行列です。
![]()
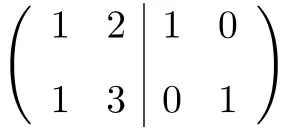
ここで、逆行列を計算するには、左側の行列を単位行列に変換する必要があります。そして、そのためには、そこに到達するまで行に変換を適用する必要があります。
すべての最初の項 1 はすでに単位行列と同じです。したがって、現時点では最初の行に変換を適用する必要はありません。
ただし、単位行列の最初の列の最後の要素には 0 があり、現在は 1 になっています。したがって、1 を 0 に変換する必要があります。これを行うには、行 2 から行 1 を減算します。
![Rendered by QuickLaTeX.com \left( \begin{array}{cc|cc}1 & 2 & 1 & 0 \\[1.5ex] 1 & 3 & 0 & 1\end{array} \right) \begin{array}{c} \\[1.5ex] \xrightarrow{f_2 - f_1} \end{array} \left( \begin{array}{cc|cc} 1 & 2 & 1 & 0 \\[1.5ex] 0 & 1 & -1 & 1\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-247d8605795c43e79b5d7742854cfe6d_l3.png)
2 番目の列に進みます。以下の 1 が適切です。ただし、単位行列のその位置には 0 があるため、上記の 2 には当てはまりません。したがって、2 を 0 に変換するには、1 行目から 2 行目と 2 を掛けた値を引きます。
![Rendered by QuickLaTeX.com \left( \begin{array}{cc|cc} 1 & 2 & 1 & 0 \\[1.5ex] 0 & 1 & -1 & 1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 - 2f_2} \\[1.5ex] & \end{array} \left( \begin{array}{cc|cc} 1 & 0 & 3 & -2 \\[1.5ex] 0 & 1 & -1 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-173a7bdb55ba058e5ae16d1fd8e91564_l3.png)
逆行列は、左側の行列を単位行列に変換した後に右側に得られる行列です。これで、左側に単位行列が得られました。したがって、逆行列は次のようになります。
![Rendered by QuickLaTeX.com \bm{A^{-1}= \left(} \begin{array}{cc} \bm{3} & \bm{-2} \\[1.5ex] \bm{-1} & \bm{1} \end{array}\bm{ \right)}](https://mathority.org/wp-content/ql-cache/quicklatex.com-98896d28465c9e1402e1c443375d93fe_l3.png)
演習 2
ガウス手順を使用して次の行列を逆行列にします。
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & 1 & -4 \\[1.1ex] 0 & 3 & 2 \\[1.1ex] 0 & 1 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7ae5ba4a92a5ddc00ddf5b11775edafd_l3.png)
まず、A 行列と恒等行列を 1 つの行列にまとめます。
![]()
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 3 & 2 & 0 & 1 & 0 \\[2ex] 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-81db2ef94d2db597cebb4c0c77685526_l3.png)
次に、左の行列を単位行列に変換するまで行を変換する必要があります。
左側の行列の最初の列はすでに単位行列の最初の列と同じです。したがって、その番号を変更する必要はありません。
ただし、単位行列の 2 番目の列の 2 番目の要素には 1 があり、そこには 3 があります。したがって、3 を 1 に変換する必要があります。これを行うには、2 行目から 3 行目を 2 倍した値を引きます。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 3 & 2 & 0 & 1 & 0 \\[2ex] 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - 2f_3} \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 1 & 4 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-bfd7cb4d4b81a75038807eb28393a83e_l3.png)
単位行列の 2 列目の最後の要素には 0 があり、現在は 1 になっています。したがって、1 を 0 に変換する必要があります。これを行うには、3 行目から 2 行目を減算します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 - f_2} \end{array} \left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-932479e2f574c19ad7906d3d20e52ad0_l3.png)
単位行列の 2 列目の最初の要素には 0 があり、現在は 1 があります。したがって、1 を 0 に変換する必要があります。これを行うには、行 1 から行 2 を減算します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 - f_2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc}1 & 0 & -4 & 1 & -1 & 2 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-566e1453aab03f9792cb281e4c88a68c_l3.png)
ここでしなければならないのは、-4 を 0 に変換することだけです。これを行うには、3 行目に 4 を掛けた値を 1 行目に追加します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & -4 & 1 & -1 & 2 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3\end{array} \right) \begin{array}{c} \xrightarrow{f_1 + 4f_3} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc}1 & 0 & 0 & 1 & -5 & 14 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6f98a9cabeb101602dd11aa73516b998_l3.png)
左側から恒等行列をすでに取得しています。したがって、逆行列は次のようになります。
![Rendered by QuickLaTeX.com \bm{A^{-1}= \left( } \begin{array}{ccc} \bm{1} & \bm{-5} & \bm{14} \\[2ex] \bm{0} & \bm{1} & \bm{-2} \\[2ex] \bm{0} & \bm{-1 }& \bm{3} \end{array} \bm{ \right)}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e43ce6a7061f0339bd5d44b83afec07f_l3.png)
演習 3
ガウス法を使用して次の行列を逆行列にします。
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & 2 & 1 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 2 & 0 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f02b0186690e68baaa9a630db2c870db_l3.png)
操作を開始する前に、A 行列と恒等行列を 1 つの行列に入れる必要があります。
![]()
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 2 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 2 & 0 & 3 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-aa6dc5af82076e22b1d0cf7ea16d748b_l3.png)
ここで、行を操作して左行列を単位行列に変換する必要があります。
最初の列の最初の 2 つの要素はすでに単位行列の要素と同じです。したがって、これらの数値を変更する必要はありません。
しかし、単位行列の最初の列の 3 番目の要素には 0 があり、そこには 2 があります。したがって、2 を 0 に変換する必要があります。これを行うには、3 行目から 1 行目と 2 を掛けた値を引きます。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc}1 & 2 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 2 & 0 & 3 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 - 2f_1} \end{array} \left( \begin{array}{ccc|ccc} 1 & 2 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & -4 & 1 & -2 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-680a314b8cc900e01886291af12145e4_l3.png)
恒等行列の 2 番目の列の最初の要素には 0 があり、そこには 2 があります。したがって、2 を 0 に変換する必要があります。これを行うには、1 行目から 2 行目を 2 倍した値を引きます。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 2 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & -4 & 1 & -2 & 0 & 1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 -2f_2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & -2 & 0\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & -4 & 1 & -2 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f87cbc594287f7ea4938091878562b4c_l3.png)
単位行列の 2 列目の最後の要素には 0 がありますが、現在は -4 になっています。したがって、-4 を 0 に変換する必要があります。これを行うには、2 行目に 4 を掛けた値を 3 行目に追加します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & -2 & 0\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & -4 & 1 & -2 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 +4f_2} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & -2 & 0\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & 0 & 1 & -2 & 4 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b8cf2c3878d2d35656953a55bb3baf94_l3.png)
ここで行う必要があるのは、3 列目の最初の要素を 0 に変換することだけです。これを行うには、行 3 に -1 を乗算した値を行 1 に追加します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc}1 & 0 & 1 & 1 & -2 & 0\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & 0 & 1 & -2 & 4 & 1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 - f_3} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc}1 & 0 & 0 & 3 & -6 & -1\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & 0 & 1 & -2 & 4 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-aac851b05c2dc25af3d7b9ecc622c9f6_l3.png)
左側の行列が単位行列であることはすでに理解しています。したがって、行列の逆行列
![]()
東:
![Rendered by QuickLaTeX.com \bm{A^{-1}= \left( } \begin{array}{ccc} \bm{3} & \bm{-6} & \bm{-1} \\[2ex] \bm{0} & \bm{1} & \bm{0} \\[2ex] \bm{-2} & \bm{4}& \bm{1} \end{array} \bm{ \right)}](https://mathority.org/wp-content/ql-cache/quicklatex.com-161fbe4a4d4dcc4fc503b6e3a9e0bfeb_l3.png)
演習 4
ガウス法を使用して次の行列を逆行列にします。
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & -2 & 0 \\[1.1ex] 1 & 2 & 2 \\[1.1ex] 0 & 3 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-47ad7ccd6aafab72255c96f2bc9148a2_l3.png)
最初に行う必要があるのは、A 行列と恒等行列を単一の行列に結合することです。
![]()
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc}1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 1 & 2 & 2 & 0 & 1 & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a832ceb9f09dfa88238c570b46b74d92_l3.png)
次に、行演算を適用して、左側の行列を単位行列に変換する必要があります。
最初の列の最初の要素はすでに単位行列の要素と同じです。したがって、変更する必要はありません。
ただし、単位行列の最初の列の 2 番目の要素には 0 があり、そこには 1 があります。したがって、1 を 0 に変換する必要があります。これを行うには、行 2 から行 1 を減算します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc}1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 1 & 2 & 2 & 0 & 1 & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 0 & 4 & 2 & -1 & 1 & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-83933b5a2315a4dcbc770bf92bf3831b_l3.png)
2 番目の列に進みます。まず 2 番目の行を 4 で割ることにより、4 を 1 に変換します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 0 & 4 & 2 & -1 & 1 & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2/4} \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-298984c72a249e2b5c98740cc0c1a11e_l3.png)
単位行列の 2 列目の最初の要素には 0 がありますが、ここには -2 があります。したがって、-2 を 0 に変換する必要があります。これを行うには、2 行目と 2 を乗算した行 2 を行 1 に追加します。

![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1\end{array} \right) \begin{array}{c} \xrightarrow{f_1 +2f_2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3dfcdcb586eed87861b3ac0ea46bea2f_l3.png)
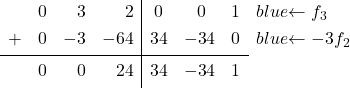
単位行列の 2 列目の最後の要素には 0 があり、そこには 3 があります。したがって、3 を 0 に変換する必要があります。これを行うには、3 行目から 2 行目と 3 を掛けた値を引きます。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -3f_2} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 0 &\sfrac{2}{4} & \sfrac{3}{4} & \sfrac{-3}{4} & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-94ed5a1b9cf1db0bfb99ce79d0a6d36b_l3.png)
3 番目の列に進みます。最後の列を変換する必要があります。
![]()
これを行うには、3 行目を 2 で乗算します。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 0 &\sfrac{2}{4} & \sfrac{3}{4} & \sfrac{-3}{4} & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{2f_3 } \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a8134938726d3b48fe3d7d789260b128_l3.png)
単位行列の最後の列の 2 番目の要素に 0 があります。したがって、変換する必要があります。
![]()
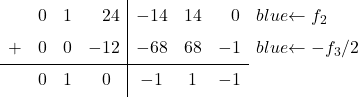
これを行うには、2 行目から 3 行目を減算し、2 で割ります。
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2-f_3/2 } \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & 0 & -1 & 1 & -1 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8b91b71183a50e41e9be5c7305f8cf3e_l3.png)
ここで行うべきことは、3 列目の最初の要素を 0 に変換することだけです。これを行うには、行 1 から行 3 を減算します。

![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc}1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & 0 & -1 & 1 & -1 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right) \begin{array}{c} \xrightarrow{f_1-f_3 } \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 0 & -1 & 2 & -2 \\[2ex] 0 & 1 & 0 & -1 & 1 & -1 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-2023374b9885dd33fe4d3c12e5a4de59_l3.png)
したがって、逆行列は次のようになります。
![Rendered by QuickLaTeX.com A^{-1}= \left( \begin{array}{ccc} -1 & 2 & -2 \\[2ex] -1 & 1 & -1 \\[2ex] \sfrac{6}{4} &\sfrac{-6}{4} & 2 \end{array} \bm{ \right)}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0854e7cb80ba561b6e0c724a9a9b5fff_l3.png)
最後に、逆行列の小数部分を簡略化できます。
![Rendered by QuickLaTeX.com \bm{A^{-1}= \left( } \begin{array}{ccc} \bm{-1} & \bm{2} & \bm{-2} \\[2ex] \bm{-1} & \bm{1} & \bm{-1} \\[2ex] \sfrac{\bm{3}}{\bm{2}} &\sfrac{\bm{-3}}{\bm{2}} & \bm{2} \end{array} \bm{ \right)}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6c7ef6b6cdca2f4a808ed9457bde3b3f_l3.png)
逆行列のプロパティ
逆行列には次のような特徴があります。
- 逆行列は一意です。
- 逆行列の逆行列は元の行列です。
![]()
- 2 つの行列の乗算の逆数は、行列の逆数の積に等しくなりますが、順序が変わります。
![]()
- 行列を転置してからその行列の逆行列を実行することは、最初に行列の逆行列を実行してからそれを転置することに似ています。
![]()
- 行列の逆行列式を解くには、行列の行列式を計算してからその逆行列を実行します。これは、2 つの演算で同じ結果が得られるためです。
![]()
2×2 行列の逆行列をすばやく計算する式
これまで見てきたように、任意の行列は行列式の方法またはガウス法によって逆行列にすることができます。ただし、これとは別に、 2×2 行列の逆行列を非常に迅速に求める公式もあります。
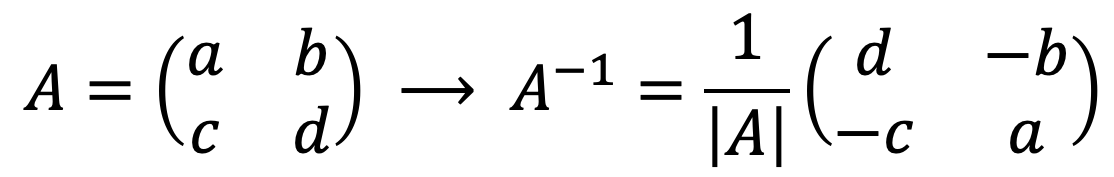
ご覧のとおり、2×2 行列の逆行列は簡単です。行列の行列式を解くだけです。
![]()
、主対角線の要素の位置を交互に変更し、副対角線の要素の符号を変更します。
数式を使用して 2 × 2 逆行列を取得する方法の例
次の 2 × 2 正方行列の逆行列を計算します。
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-599baee27c05b5610a8714363e1260eb_l3.png)
行列 A の行列式は次のとおりです。
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} 3 & 5 \\[1.1ex] -2 & -4 \end{vmatrix} & = 3 \cdot (-4)- (-2) \cdot 5 \\ & = -12-(-10) \\[2ex] & =-12+10\\[2ex] &=-2\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ab99f7b87d01c670a8598df6364ab58f_l3.png)
ここで、逆行列の公式を適用します。
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d5308484309da4485a3d9b92af86e7d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{-2} \begin{pmatrix} -4 & -5 \\[1.1ex] 2 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-68fd6e830b576af8abf55be1e11fbafb_l3.png)
そして、行列に分数を掛けます。
![Rendered by QuickLaTeX.com \displaystyle A^{-1} =\begin{pmatrix} \cfrac{-4}{-2} & \cfrac{-5}{-2} \\[3ex] \cfrac{2}{-2} & \cfrac{3}{-2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-41da8ef6bef1d339337717ed4ad86ae5_l3.png)
したがって、逆行列 A は次のようになります。
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =}\begin{pmatrix} \bm{2} & \cfrac{\bm{5}}{\bm{2}} \\[3ex] \bm{-1} & \bm{-}\cfrac{\bm{3}}{\bm{2}} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-29da2a64f6da927857de112ca8363ba5_l3.png)
ご覧のとおり、この式を使用した行列の反転ははるかに高速ですが、次元 2×2 の行列に対してのみ使用できます。
次の公式を使用した 2×2 逆行列の演習を解決しました。
演習 1
次の次元 2×2 の行列を反転します。
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 2 & 5 \\[1.1ex] 1 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dc06e21fc1c3c54f9b3fc0dcd4912a8f_l3.png)
行列 A の行列式は次のとおりです。
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} 2 & 5 \\[1.1ex] 1 & 3 \end{vmatrix} & = 2 \cdot 3- 1 \cdot 5 \\ & = 6-5 \\[2ex] & =1\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1b0ae510ea7a336cbe5ea56a554da719_l3.png)
ここで、公式を適用して逆行列を見つけます。
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d5308484309da4485a3d9b92af86e7d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 2 & 5 \\[1.1ex] 1 & 3 \end{pmatrix} \longrightarrow A^{-1} = \cfrac{1}{1} \begin{pmatrix} 3 & -5 \\[1.1ex] -1 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b8f18178c829fd38360a04a947d52017_l3.png)
したがって、行列 A の逆行列は次のようになります。
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =}\begin{pmatrix} \bm{3} & \bm{-5} \\[1.1ex] \bm{-1} & \bm{2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-237fe82cd91972f667f6751fa4735534_l3.png)
演習 2
次の 2 次行列の逆行列を計算します。
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 2 & 6 \\[1.1ex] -1 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f2289d1c5c9aeb87016f719305d900a7_l3.png)
行列 A の行列式は次のとおりです。
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} 2 & 6 \\[1.1ex] -1 & -2 \end{vmatrix} & = 2 \cdot (-2)- (-1) \cdot 6 \\ & = -4-(-6) \\[2ex] & =-4+6 \\[2ex] & =2\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a3fef2cc00702131123994cc588bf7ea_l3.png)
次に、次の公式を適用して次元 2×2 の逆行列を解きます。
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d5308484309da4485a3d9b92af86e7d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 2 & 6 \\[1.1ex] -1 & -2 \end{pmatrix} \longrightarrow A^{-1} = \cfrac{1}{2} \begin{pmatrix} -2 & -6 \\[1.1ex] 1 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2de7166a0cf59e0f8c5b7750e1947f04_l3.png)
そして最後に、乗算を行います。
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \cfrac{-2}{2} & \cfrac{-6}{2} \\[3ex] \cfrac{1}{2} & \cfrac{2}{2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f6a5973078468914beb4bd4d85a40331_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =}\begin{pmatrix} \bm{-1} & \bm{-3} \\[2ex] \cfrac{\bm{1}}{\bm{2}} & \bm{1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a540a077ee9a24da96fa988410aef429_l3.png)
演習 3
次の 2×2 行列を反転します。
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-36e230a808c42411a9cfd2d9eb44543d_l3.png)
行列 A の行列式は次のとおりです。
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} 4 & 1 \\[1.1ex] 5 & 2\end{vmatrix} & = 4 \cdot 2 - 5 \cdot 1 \\ & = 8-5 \\[2ex] & =3\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e7a6c5ef316ae51b43c90863c6245780_l3.png)
次に、次の式を適用して次元 2×2 の逆行列を計算します。
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d5308484309da4485a3d9b92af86e7d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix} \longrightarrow A^{-1} = \cfrac{1}{3} \begin{pmatrix} 2 & -1 \\[1.1ex] -5 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e2f359bd166c295b869a8cf04d927097_l3.png)
最後に、分数と行列の積を計算します。
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \cfrac{\bm{2}}{\bm{3}} & \bm{-}\cfrac{\bm{1}}{\bm{3}} \\[3ex] \bm{-}\cfrac{\bm{5}}{\bm{3}} & \cfrac{\bm{4}}{\bm{3}} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6a02ea2e547dcc21081ae80df407a4e0_l3.png)
演習 4
次の 2 次行列の逆行列を求めます。
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} -2 & 5 \\[1.1ex] -3 & 10 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-422fcd6f391a2682e4b546c9e9c05b55_l3.png)
行列 A の行列式は次のとおりです。
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} -2 & 5 \\[1.1ex] -3 & 10\end{vmatrix} & = (-2) \cdot 10- (-3) \cdot 5 \\ & = -20-(-15) \\[2ex] & =-20+15 \\[2ex] & =-5\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e9997751e16d3b976454be828cb914d_l3.png)
次に、数式を適用して次元 2×2 の逆行列を作成します。
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d5308484309da4485a3d9b92af86e7d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} -2 & 5 \\[1.1ex] -3 & 10\end{pmatrix} \longrightarrow A^{-1} = \cfrac{1}{-5} \begin{pmatrix} 10 & -5 \\[1.1ex] 3 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7c0c614039614bd9125b2920da8698eb_l3.png)
そして最後に、乗算を行います。
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \cfrac{10}{-5} & \cfrac{-5}{-5} \\[3ex] \cfrac{3}{-5} & \cfrac{-2}{-5} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-edb1dfc870b3045eaefc1716a80e2ca2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =}\begin{pmatrix} \bm{-2} & \bm{1} \\[2ex] \bm{-}\cfrac{\bm{3}}{\bm{5}} & \cfrac{\bm{2}}{\bm{5}} \ \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5c49e161c701254cfbe20353c11980eb_l3.png)
逆行列を使用して連立方程式を解く
逆行列の実際の応用を理解するのは困難です。実際、あなたはおそらく疑問に思っているでしょう…逆行列は何に使用されるのでしょうか?本当に何かに使われているのでしょうか?
逆行列の用途の 1 つは、連立一次方程式を解くことです。はい、これらは 2 つの非常に異なる概念のように見えるかもしれませんが、行列を反転することによって方程式系の解を見つけることができます。
これがどのように行われるかを例で見てみましょう。
- 逆行列を使用して、次の連立方程式の解を計算します。
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+3y=5 \\[2ex] 2x+4y=6 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-200c0f994f86752e7d650621a0d4100f_l3.png)
まず第一に、方程式系は行列の形式で表現できることに注意する必要があります。
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 4 \end{pmatrix}\begin{pmatrix} x \\[1.1ex]y \end{pmatrix} = \begin{pmatrix} 5 \\[1.1ex] 6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4b9c9f181fc16a501799145c516a9747_l3.png)
システムのこの行列形式が方程式による式と同等であることを検証できます。行列を乗算すると、システムの 2 つの方程式が得られることがわかります。
ここで、次のステップを簡略化するために、次のように呼び出します。
![]()
未知数の係数を持つ行列に、
![]()
未知数を含む行列の列に、
![]()
独立項を含む列行列に変換するには、次のようにします。
![]()
したがって、マトリックスは
![]()
は行列方程式の未知数です。
この行列方程式を解くには、ここでは詳しく説明しない手順に従う必要があります。完全に理解したい場合は、 行列を使用して方程式を解く方法を確認してください。プロセス全体を段階的に説明しています。
この手順は、逆行列の特性に基づいています。つまり、行列にその逆行列を乗じたものは、Identity (または Unit) 行列に等しくなります。したがって、未知の行列を簡単に解くことができます。
![]()
方程式の両辺に行列 A の逆数を乗算します。
![]()
![]()
![]()
![]()
マトリックスを分離したら
![]()
の逆数を計算します。
![]()
そして行列の積を解きます。
![Rendered by QuickLaTeX.com \displaystyle X=\left.\begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 4 \end{pmatrix}\right.^{-1}\cdot \begin{pmatrix} 5 \\[1.1ex] 6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9a1290e37a9e3f56fc6b288bc7686d66_l3.png)
![Rendered by QuickLaTeX.com \displaystyle X=\cfrac{1}{-2} \begin{pmatrix} 4 & -3 \\[1.1ex] -2 & 1 \end{pmatrix}\cdot \begin{pmatrix} 5 \\[1.1ex] 6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-21471fc8a4c04aac3121519e8ef874e5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle X= \begin{pmatrix} -1 \\[1.1ex] 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b9457fedf68c4bdfea898922e465eeb8_l3.png)
したがって、連立方程式の解は次のようになります。
![]()