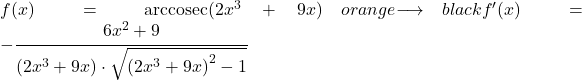このページでは、逆正割の導関数の公式がどのようなものかがわかります。さらに、関数のアークコセカントの導関数の解答済み演習も表示されます。
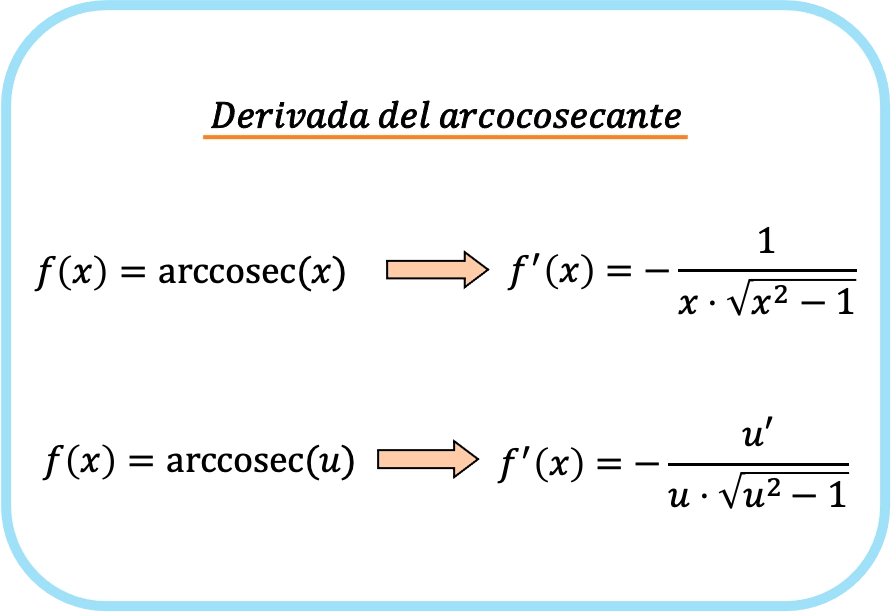
逆正割微分公式
x の逆正割の導関数は、x と x の二乗根から 1 を引いた積の負の 1 になります。
![]()
したがって、関数の逆正割の微分値は、その関数の微分値を関数で割った商に、その関数の平方根を掛けて 1 を引いたものに等しくなります。
![]()
実際、前の 2 つの式は同じですが、2 番目の式では連鎖規則が適用されます。実際、恒等関数 x を u に代入すると、x の導関数は 1 であるため、x の逆正割の導関数が得られます。
ご存知のとおり、逆余割は余割の逆三角関数ですが、その導関数はまったく異なります。この他のタイプの三角関数の公式は、次のリンクで確認できます。
➤参照: コセカントの導関数
コセカントアークの導関数の例
逆正割導関数の規則が何であるかを見て、次にこのタイプの導関数の 2 つの例を解きます。ただし、コセカントアークの導出方法についてまだ質問がある場合は、コメントで質問してください。
例1
この例では、二次関数 x 2の逆余割の微分がどのくらいになるかを確認します。
![]()
x の 2 乗の逆正割の導関数を計算するには、上で見た式を適用します。
![]()
x の 2 乗の導関数は 2x であるため、複合関数の導関数は次のようになります。
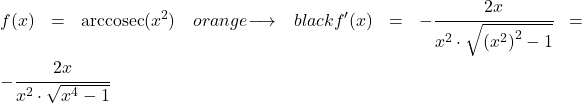
例 2
この 2 番目の例では、ポテンシャル関数の逆正割を導出します。
![]()
関数全体の導関数を見つけるには、アークセカント導関数ルールを使用する必要があります。
![]()
したがって、分子に関数の引数の導関数を書き、分母にポテンシャル関数を書き直して、引数の 2 乗から 1 を引いた関数の平方根を掛けます。