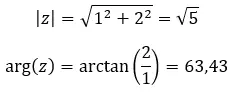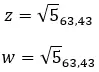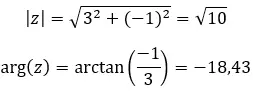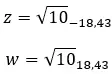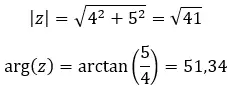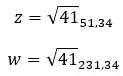この記事では、計算を解くときや式を簡略化するときに役立つ複素数の性質について説明します。これらのプロパティに直接進みましょう。
複素数の法と引数
複素数の最初のプロパティは、複素数の法と引数です。いくつかの式を適用するだけなので、計算は非常に簡単です。
モジュールを計算する式は次のとおりです。

引数を計算する式は次のとおりです。

ここで、数値が極形式または三角形式で表現されている場合は、計算を行う必要はありません。同じ式の中にモジュールと引数がリストされているためです。
下の画像では、数値の公式を極形式で見ることができます。ここで |z|は係数、α は引数です。

そして、この別の画像では、三角関数形式で表現された数値の構造を見ることができます。は係数、α は引数です。

等しい複素数
等しい複素数は、法と引数を共有する複素数です。したがって、これら 2 つの値から次のようになります。

以下の性質を満たす場合も同様です。
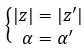
一方、両方の数値が二項形式である場合、それらが 2 つの等しい複素数であるかどうかを非常に迅速かつ簡単にチェックできます。単純に、次の式を満たす必要があります。
a + ビ = a + ビ
例を見て、次の 2 つの複素数が等しいかどうかを判断してみましょう。
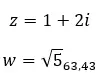
共役複素数
さて、複素数の最も重要な性質の 1 つに移りましょう。複素数の共役の計算方法を知っていると、複素数の除算を解いたり単純化するのに非常に役立ちます。
したがって、これら 2 つの値から次のようになります。

それらがモジュールを共有し、反対の引数を持つ場合、それらは共役であると言います。したがって、次のように完了する必要があります。
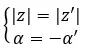
一方、両方の数値が二項形式である場合、それらが 2 つの複素共役数値であるかどうかを非常に迅速かつ簡単にチェックできます。単純に、次の式を満たす必要があります。
アン + ビ = アン – ビ
例を見て、次の 2 つの複素数が共役かどうかを確認してみましょう。
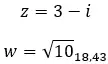
複素数の反対
次に、反対の複素数の性質を見てみましょう。これら 2 つの値から:

同じモジュールを持ち、引数が 180 度または π ラジアンだけ異なる場合、それらは反対であると言えます。
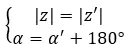
一方、両方の数値が二項形式である場合は、別のさらに高速かつ簡単な方法を使用して、それらが 2 つの反対の複素数であるかどうかを確認できます。単純に、次の式を満たす必要があります。
a + ビ = -a – ビ
例を見て、次の 2 つの複素数が反対かどうかを判断してみましょう。
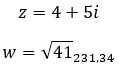
その他のプロパティ
明らかに、この数値セットには、逆複素数や基本的な算術演算に直接関連するその他のいくつかのプロパティなど、他のプロパティもあります。これらはすべて他の記事で説明されていますが、以下のリストで確認できます。
複素数の性質について学ぶ
- 複素数
- 複素数の演算
- 複雑な根
- 複素数のグラフィック表現