おそらく複素数について聞いたことがあるでしょう。これらは実数と虚数を組み合わせたものであるため、おそらく扱うのが最も難しい数値のセットです。その統合により、すべての実数を使用して扱うことができない数値的動作を研究することが可能になります。
複素数とは何ですか?
複素数は、実数と虚数の組み合わせです。たとえば、 4 + 5i は、4 に等しい実数部と 5i に等しい虚数部を持つ複素数です。一般に、これらは次の式で表すことができます。
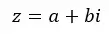
ここで、Re(z) = a および Im(z) = b
よく言ったように、複素数は実数と虚数の両方を含む最大の集合またはグローバル集合です。次に、すべてのセットの階層構造を示す小さな図を示します。

したがって、実数と虚数を組み合わせると複素数が得られます。ただし、2 つの部分のうちの 1 つがゼロに等しい場合があります。このような場合はどうなるのでしょうか?複素数セットには他のすべての数値セットが含まれるため、引き続き複素数を扱います。ただし、別のサブカテゴリに入ります。
| 複素数 | ロイヤルパーティー | 想像の部分 | サブカテゴリ |
| 2+5i | 2 | 5i | 複雑な |
| 4 | 4 | 0 | 純粋なロイヤル |
| 3i | 0 | 3i | 純粋な想像力 |
純粋な実数がある場合、虚数 b はゼロに等しいため、残りの複素数は次と等価です。
z = a + 0i = a
一方、純粋な想像力がある場合、a はゼロに等しいため、複素数は次のとおりです。
z = 0 + bi = bi
複素数のグラフィック表現
複素数を表すには、複素平面を使用します。実線と虚数線の2本の線で構成されています。これら 2 つの数直線は、各セット内の数値をグラフィカルに見つけるために使用され、それらを組み合わせると、次のような計画が得られます。

X 軸は実数部の値が配置されるため、実数軸と呼ばれます。 Y 軸は虚数軸と呼ばれますが、ここには虚数が書き込まれます。例を見てみましょう。数値3 + 2iを複素平面に配置します。

画像で見たように、数値 3 と 2 をそれぞれ軸の座標として使用して、数値を特定しました。複素数の表現について詳しく知りたい場合は、この記事を読むことをお勧めします。
複素数にはどのような種類があるのでしょうか?
ここで、複素数を表現する方法を見てみましょう。ここまでは、実数部と虚数部の合計として記述される基本形式 (二項形式と呼ばれる) のみを見てきました。
しかし、実際には、二項、極、三角の3 つの形式があります。それぞれのタイプの式にはそれぞれの特性があり、さまざまな状況で使用されます。そこで、それらすべてを説明し、一方から他方へ移行する方法を示します。
1. 二項形式
二項形式の複素数は、実数部と虚数部の和、つまり a + bi として記述されます。たとえば、数値 6 + i は、二項表記で表現される複素数です。この例では、式は常に同じです。

したがって、複素数を二項形式で表現するには、その実数値と虚数値だけを知る必要があります。
たとえば、値3 + 2iは二項形式であり、前に見たように、次のように表されます。

二項形式は主に複素数の加算と減算を解くために使用されます。
2. 極形式
複素数を極形式で表現するには、そのモジュール |z| を計算する必要があります。そして彼の主張。極形式は主に、複素数の乗算と除算を解く必要がある場合に使用されます。
複素数の係数を計算するには、次の式で説明されているように、a と b の係数を計算するだけです。

そして、z の引数または角度を計算するには、a 間の b の逆正接を計算する必要があります。

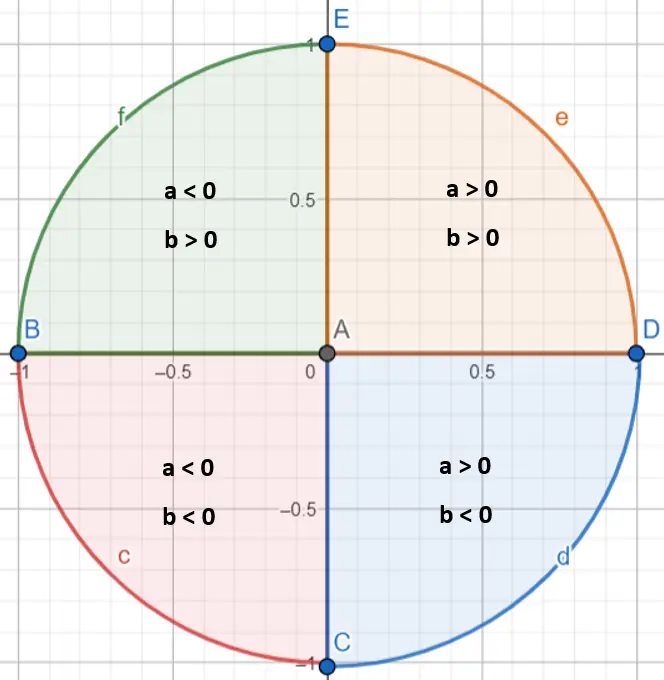
角度 α の値を正確に決定するには、角度 α がどの象限に位置するかを特定する必要があることに注意することが重要です。実際、逆正接関数は π/2 と -π/2 の間の角度のみを計算します。複素数がどの象限に位置するかを指定するには、値 a と b (正か負か) を確認する必要があります。
数値がどの象限に該当するかがわかったら、いくつかのルールに従う必要があります。
- 複素数が第 1 象限 (a > 0 および b > 0) にある場合は、引数をそのままにしておきます。
- 複素数が第 2 象限 (a < 0 および b > 0) にある場合、引数に π を追加します。
- 複素数が第 3 象限 (a < 0 および b < 0) にある場合、引数から π を減算します。
- 複素数が第 4 象限 (a > 0 および b < 0) にある場合、引数に 2π を追加します。
四分円と言うときに何を言っているのかわからない場合は、三角比に関する記事を参照することをお勧めします。
z の大きさと引数がわかれば、複素数を極形式で表現できます。この形式ではいくつかの命名法が受け入れられますが、主なものは次の 2 つです。

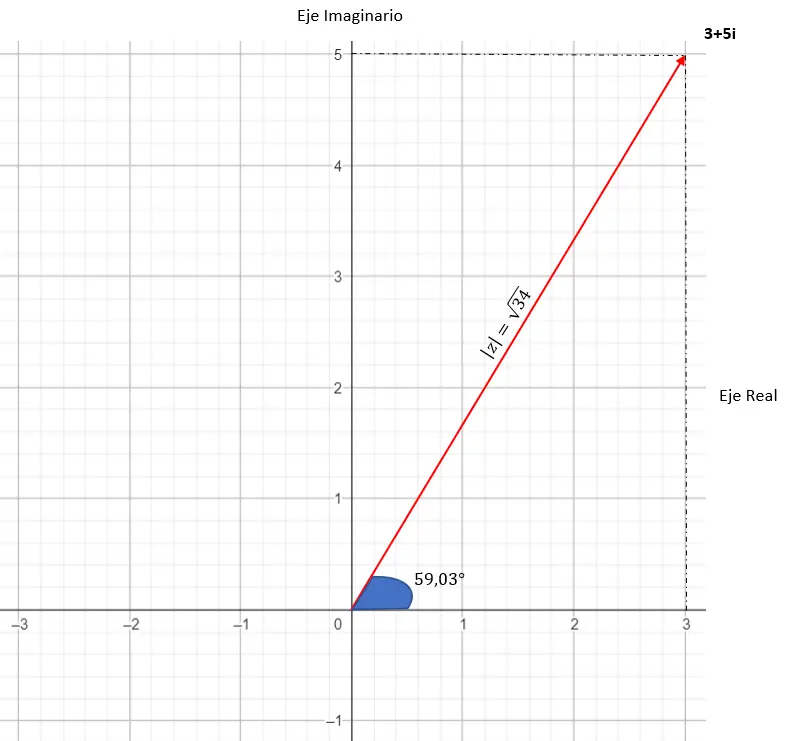
たとえば、数値3 + 5i を極座標に変更したい場合は、次の手順に従うだけです。
まずモジュールを計算します。
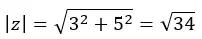
次に、第 1 象限にある引数を計算します。したがって、計算したとおりになります。
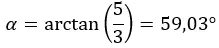
そして、数値を極形式で表現します。
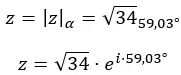
そのグラフィック表現は次のとおりです。
3. 三角関数の形式
最後に、 オイラーの公式から計算される三角関数表記があります。

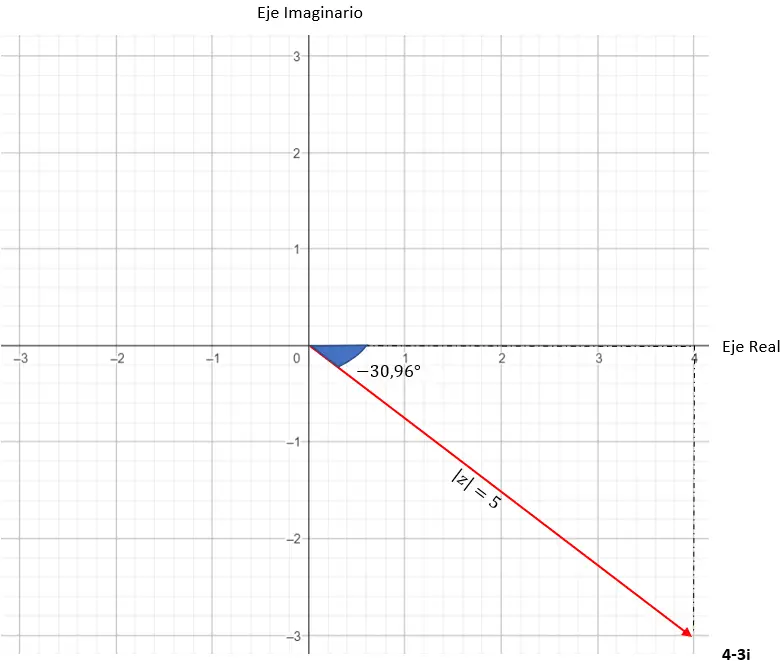
たとえば、数値 4 – 3i を三角関数形式で表現するには、次の手順に従います。
まず、極形式のセクションで使用した式を使用して係数と引数を計算します。
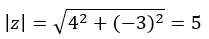
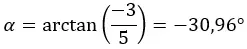
注意: (a > 0 および b < 0) であるため、引数は第 4 象限にあります。
データを三角関数形式で方程式に追加します。
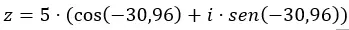
そして、すでに三角関数形式で表された数値が得られています。その図式表現は次のとおりです。
あるタイプから別のタイプに切り替えるにはどうすればよいですか?
これで、複素数を表現するすべての方法がわかりました。最後のセクションでは、それぞれのフォームにアクセスする方法を説明しましたが、終了する前に、あるフォームから別のフォームに移動する方法について簡単にまとめておきたいと思います。前のセクションで説明した式を使用するだけで済みます。
二項形式から極形式へ、またはその逆へ
二項から極に移行するには、次の図を提案します。
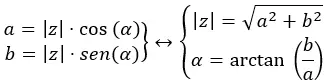
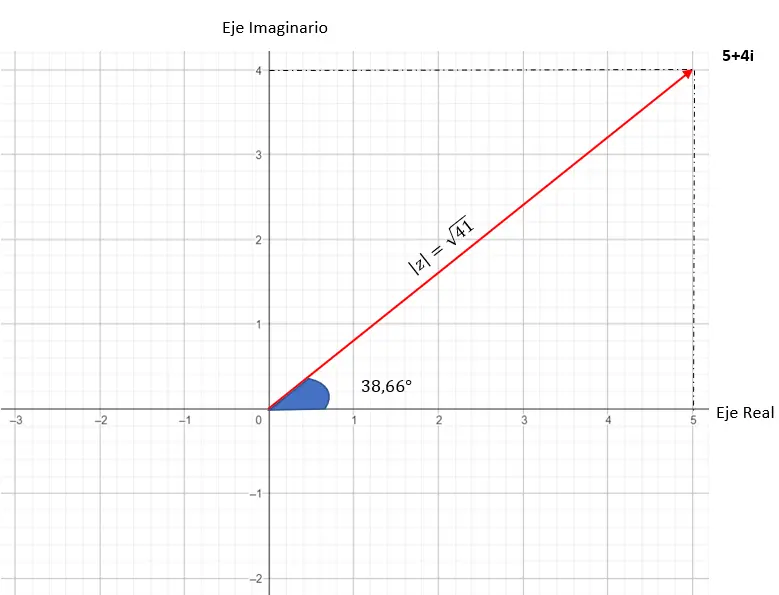
前に二項から極に移行する例を見たので、今度は上の図を使用して極から二項に移行します。 √41 38.66を二項式に変換する必要があります。
まず a を計算します。
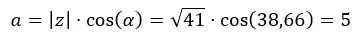
次に b を計算します。
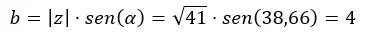
そしてそれを二項形式で表現します。
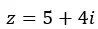
この数値をグラフで表すと次のようになります。
二項形式から三角形式へ、またはその逆
二項関数から三角関数に移行するには、前のセクションで説明した公式も適用する必要があります。このようにして、最初に係数と引数を計算し、次にこのデータを三角関数の方程式に代入します。例として、数値z = 3 + 2i を三角関数的に渡します。
まず、係数と引数を計算します。
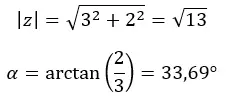
注意: (a > 0 および b > 0) であるため、引数は第 1 象限にあります。
次に、このデータを使用して三角関数の形式の方程式を完成させます。
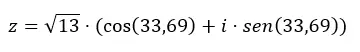
そして、三角関数から二項関数に移行したい場合は、前の式を解くだけで済みます。
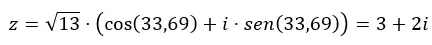
極形式から三角形式へ、またはその逆へ
最後に、極形式から三角形式に移行します。これら 2 つの形式は同じ 2 つの値、 modulo と argumentで表現されるため、これは非常に簡単です。したがって、フォームに記入するだけで完了です。
例を挙げてみましょう。数値z = √85 12.53を三角関数形式に変換します。
三角関数形式の方程式の 2 つの変数 (モジュールと引数) を再定式化します。
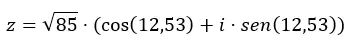
あるフォームから別のフォームに移行する方法がわかったので、いくつかの演習で少し練習することをお勧めします。こうすることで、この記事で学んだ知識を定着させることができます。このトピックに関してご質問がございましたら、お気軽にコメント欄に残してください。複素数についてさらに詳しく知りたい場合は、以下のリンクをチェックしてください。
複素数に関する詳細情報
- 虚数
- 複素数の性質
- 複素数の演算
- 複素数の根
- 複素数のグラフィック表現