複素数は、実数と虚数から構成されるセットです。これらの最後の 2 つの数値セットは、実線と虚数線を使用してグラフで表すことができます。そして、両方の線を同じ平面上に配置すると、よく知られている複素平面が形成されます。
複雑な計画とは何ですか?
複素平面は、実線に相当する実軸(X軸)と、仮想線を概念化した虚軸(Y軸)によって形成されます。
この計画にはすべての複素数が含まれていることに注意してください。したがって、どんなに小さくても、どんな形で複素数を書いても、それを図面上でグラフィカルに表現することができます。それでは、これらの数値が複素平面でどのように表現されるかを見てみましょう。
複素数を複素平面上にグラフ化するにはどうすればよいですか?
すでにご存知のとおり (知らない場合は、複素数に関する記事を読むことをお勧めします)、複素数を記述するには、二項形式、極形式、三角形式の 3 つの方法があります。それぞれが異なる構造に従って複素数値を表現するため、グラフィック表現を作成するための方法が異なります。
次に、3 つの場合に従う手順を説明します。
二項形式での表現
最も一般的な二項表記の複素数がある場合、その数値の構造を調べる必要があります。

ここで、a は実数部、b は虚数部です。
これを知っていると、a の値は横軸 (実軸) に使用する値であり、b の値はコンピューターに使用する値 (虚数軸) であると推測されます。次の例を見ると、よりよく理解できるでしょう。
3 + 2i という数字を表現してみます。
最初にグラフを描画します (横軸が実数軸、縦軸が虚数軸であることに注意してください)。

次に、複素数から推定されるデカルト座標 (x, y) でグラフの点を特定します。この実際の例では、ポイントは (3, 2) です。
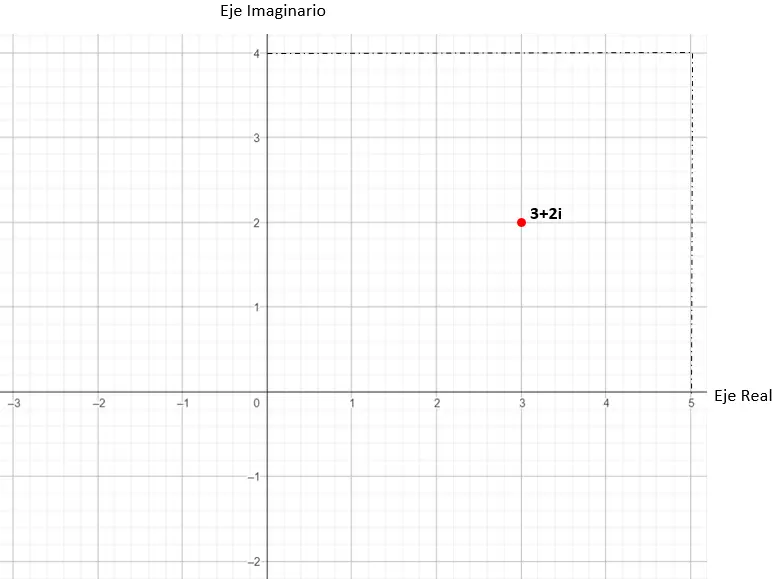
したがって、値 3 + 2i は複素平面で表現されます。
極形式での表現
ここで、複素数が極形式でどのように表現されるかを見てみましょう。この方法を完全に理解するには、極表記がモジュールと引数に基づいて複素数を定義することを知っておく必要があります。これらは、グラフ表現では極座標として (デカルト座標としてではなく) 使用されます。
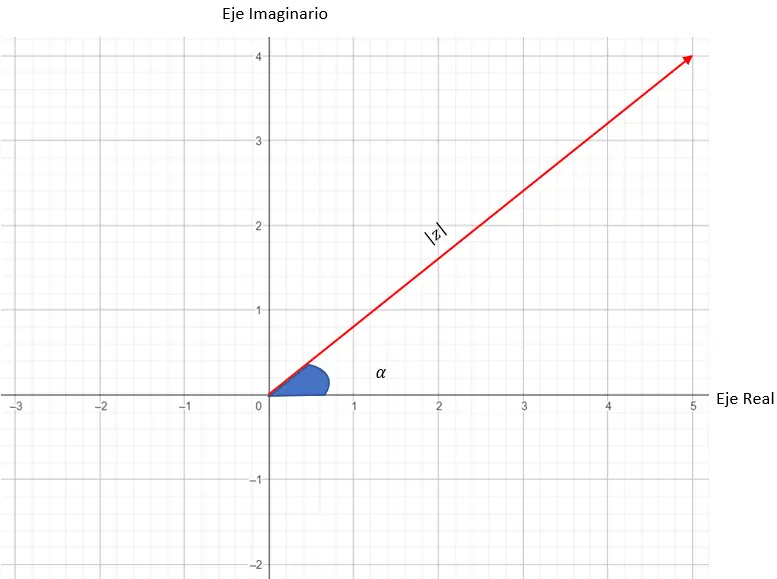
そして、極座標系の主な特徴は、点の位置がベクトルと角度によって記述されることです (以前の方法とは異なります)。複素数のモジュールと引数に対応します。次に、複素数の極形式の普遍的な公式を示します。

ここで |z|は係数、α は引数です。これら 2 つの変数は、計画内で次のように変換されます。
- モジュール:ベクトル (原点と数値に相当する点の間) を定義する長さです。
- 引数:ベクトルが X 軸となす角度です。
したがって、複素数の法は、グラフの作成に使用するベクトルの長さに対応します。一方、複素数の引数または角度は、ベクトルと X 軸の間の角度です。以下に、すべての変数を配置した図を示します。
ここで、数値 3 45を表現してみます。
まず、モジュールと引数を特定する必要があります。
- モジュール: 3.
- 引数: 45 度。
次に、係数が 3 に等しいグラフ上の点を見つける必要があります。この場合、半径 3 の円上の任意の点が機能します。
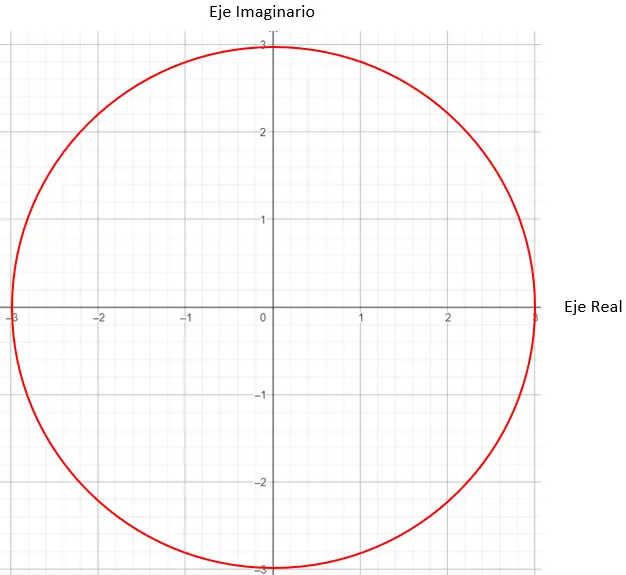
そして、正確な点が何であるかを決定するには、モジュールによって生成されたベクトルと原点が X 軸に対して 45 度の角度をなす必要があるという条件を設定する必要があります。
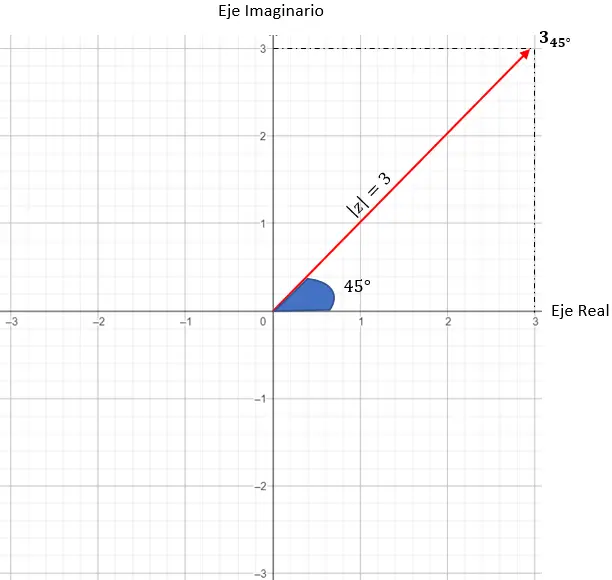
そして、極表記で表現された複素数がすでにあります。
三角関数形式での表現
最後に、複素数が三角関数形式でどのように表現されるかを説明する必要があります。このケースと前のケースは実質的に同じです。極形式と三角形式は複素数を表すために同じデータ、つまり係数と引数を使用するためです。これは式の構造のみを変更します。

ここで、|z|は係数、α は引数です。
したがって、前の場合と同じ方法を利用する必要があります。つまり、モジュールを「長さ」として使用し、引数を角度として使用します。次の例を見ると、よりよく理解できるでしょう。
z = 4 · (cos (45) + i · sin(45)) と表します。
最初にモジュールと角度を特定します。
- モジュール: 4.
- 引数: 45 度。
次に、係数が 4 に等しいグラフ上の点を見つける必要があります。この場合、半径 4 の円上の任意の点が機能します。
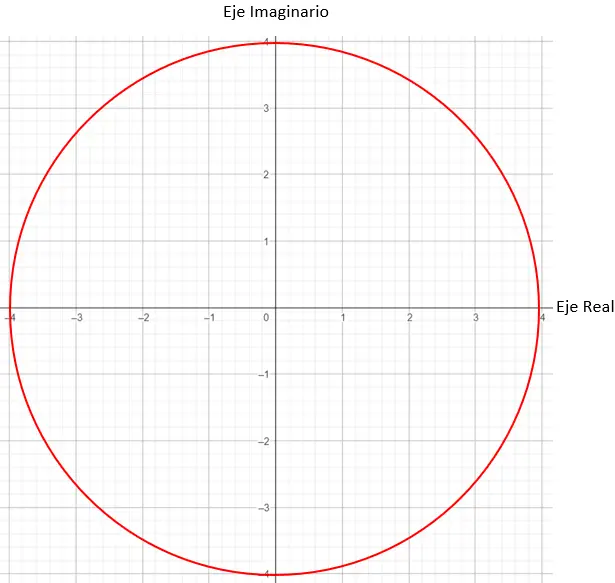
そして最後に、引数が示すように、係数ベクトルと X 軸の間に形成される角度が 45 度であることを必要として、正確な点を特定します。
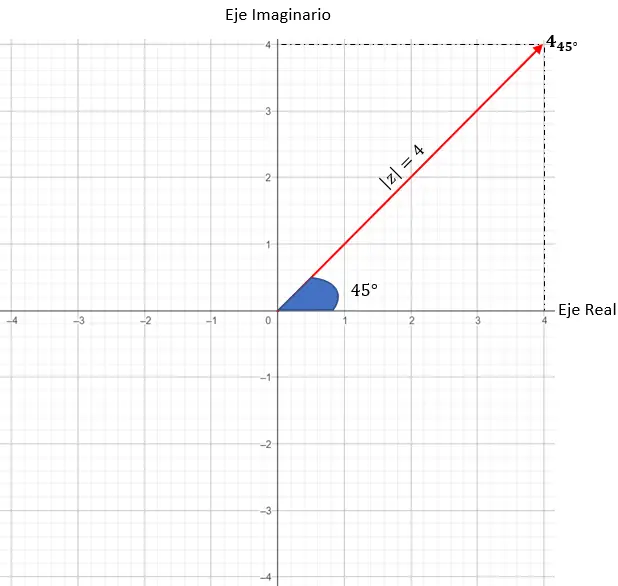
したがって、複素数を三角関数形式で表します。
複雑な飛行機の訓練
この出版物を締めくくるために、最後の演習を 1 つ提案します。この記事全体で説明されている知識を定着させるため、この問題を解決することを強くお勧めします。
次の 3 つの複素数の複素平面上のグラフィック表現の証明:
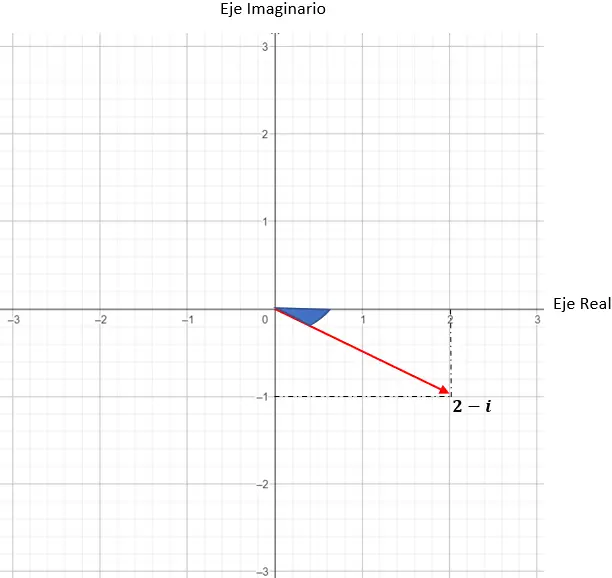
z = 2 – i
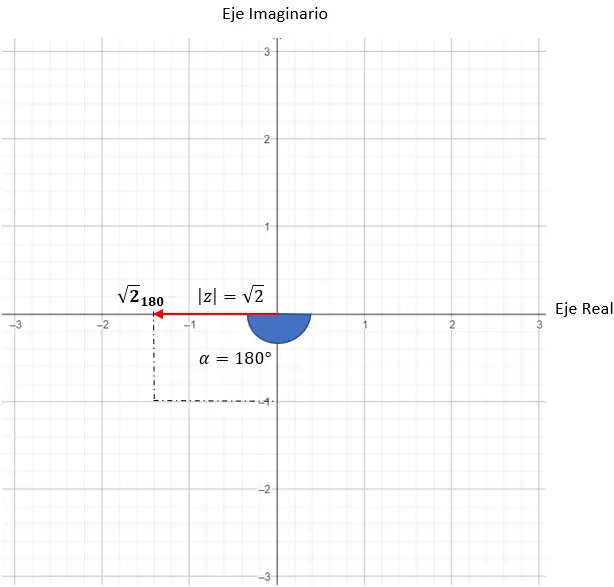
w = √2180
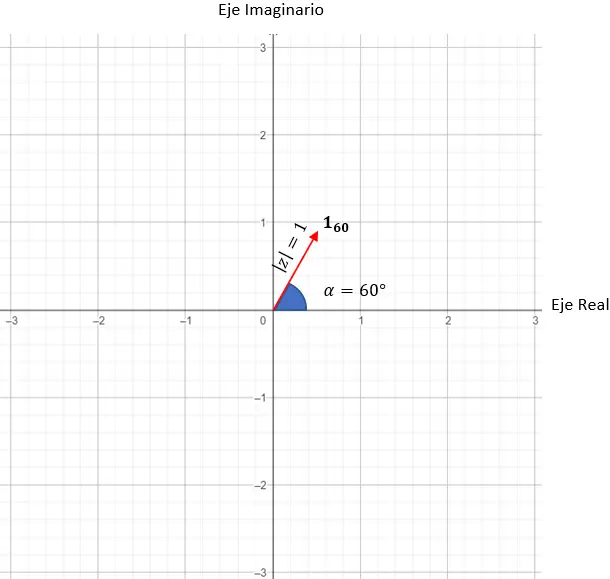
p = cos(60) + I sin(60)