このページでは、2×2 行列の行列式とは何かを学びます。さらに、次数 2 の行列式を解く方法に関する段階的な解決例と演習が含まれているため、練習して完全に理解することができます。
2×2行列式とは何ですか?
次数 2 の行列式は、行列の各辺の垂直バーで表される 2 × 2 次元の行列です。たとえば、次の行列があるとします。
![\displaystyle A = \begin{pmatrix} 3 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-50ff006696d04e4eee005e245ba217e4_l3.png "Rendered by QuickLaTeX.com")
行列 A の行列式は次のように表されます。
![\displaystyle \lvert A \rvert = \begin{vmatrix} 3 & 1 \\[1.1ex] 5 & 2 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3dc95ca8f173419691852fd137d67154_l3.png "Rendered by QuickLaTeX.com")
ご覧のとおり、2×2 正方行列の行列式を書くのは簡単です。では、どのように計算されるかを見てみましょう。
次数 2 の行列式を解くにはどうすればよいでしょうか?
2×2 行列の行列式を計算するには、主対角要素を乗算し、副対角要素の積を減算する必要があります。
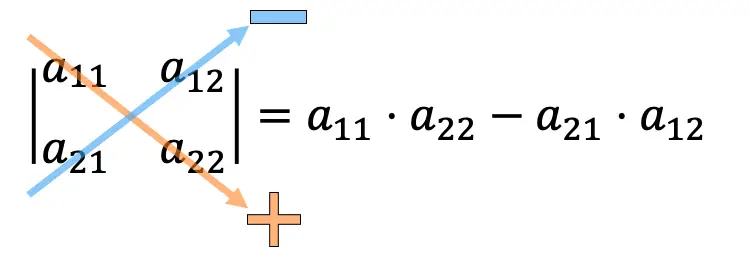
2×2 行列式の計算例:
![\displaystyle\begin{vmatrix} 3 & 4 \\[1.1ex] 2 & 1 \end{vmatrix} = 3 \cdot 1 - 2 \cdot 4 = 3 - 8 = \bm{-5}](https://mathority.org/wp-content/ql-cache/quicklatex.com-228cbdabc4e6d330b56fae20f5163e64_l3.png "Rendered by QuickLaTeX.com")
![\displaystyle\begin{vmatrix} 2 & -3 \\[1.1ex] 1 & 5 \end{vmatrix} = 2 \cdot 5 - 1 \cdot (-3) =10-(-3) = 10+3= \bm{13}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5e9aed81d00e74873a5e797746861a51_l3.png "Rendered by QuickLaTeX.com")
2 × 2 行列の行列式の問題を解決しました
演習 1
次の 2×2 行列式を計算します。
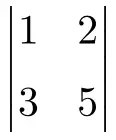
解決策を参照
2×2 行列式を作成するには、主対角要素を乗算し、副対角要素の積を減算する必要があります。
![\displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 3 & 5 \end{vmatrix} = 1 \cdot 5 - 3 \cdot 2 = 5 - 6 = \bm{-1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8d03764083647c0b05f9a5d7266c8915_l3.png "Rendered by QuickLaTeX.com")
演習 2
次の次元 2×2 の行列式を解きます。
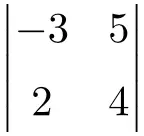
解決策を参照
次数 2 の行列式の解を求めるには、主対角要素を乗算し、副対角要素の積を減算する必要があります。
![\displaystyle \begin{vmatrix} -3 & 5 \\[1.1ex] 2 & 4 \end{vmatrix} = -3 \cdot 4 - 2 \cdot 5 = -12 - 10 = \bm{-22}](https://mathority.org/wp-content/ql-cache/quicklatex.com-56c917d70b8c6ec3697612d44f84e522_l3.png "Rendered by QuickLaTeX.com")
演習 3
次の次数 2 の行列式の解を求めます。
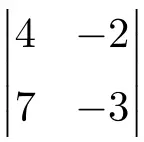
解決策を参照
次元 2 の行列式の解を求めるには、主対角要素を乗算し、副対角要素の積を減算する必要があります。
![\displaystyle \begin{vmatrix} 4 & -2 \\[1.1ex] 7 & -3\end{vmatrix} = 4 \cdot (-3) - 7 \cdot (-2) = -12 - (-14) =-12+14= \bm{2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cbd06fd83283d3e82105c24eaf95af9f_l3.png "Rendered by QuickLaTeX.com")
演習 4
次の 2×2 行列式を計算します。
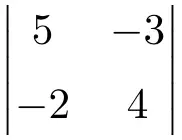
解決策を参照
2×2 行列の行列式を計算するには、主対角要素を乗算し、副対角要素の積を減算する必要があります。
![\displaystyle \begin{vmatrix} 5 & -3 \\[1.1ex] -2 & 4\end{vmatrix} = 5 \cdot 4 - (-2) \cdot (-3) = 20 - (+6) = \bm{14}](https://mathority.org/wp-content/ql-cache/quicklatex.com-34915d9aff298587a13346c6fc30bfcd_l3.png "Rendered by QuickLaTeX.com")
演習 5
次の 2×2 行列式の結果を求めます。
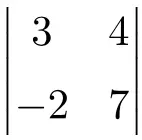
解決策を参照
2×2 行列式の解を見つけるには、主対角要素を乗算し、副対角要素の積を減算する必要があります。
![\displaystyle \begin{vmatrix} 3 & 4 \\[1.1ex] -2 & 7\end{vmatrix} = 3 \cdot 7 - (-2) \cdot 4 = 21 - (-8)=21+8 = \bm{29}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4c6e4a7fdc04f0458d95c1d62b12d7ac_l3.png "Rendered by QuickLaTeX.com")
明るい！次元 2×2 の行列式を作成する方法がわかりました。これで、 3×3 行列式がどのように計算されるか、また4×4 行列の行列式がどのように解かれるかはすでに理解できたと思います。