このセクションでは、行列式のすべての性質が何であるかを見ていきます。また、各プロパティを完全に理解できるように、例を使用して説明します。さらに、決定子のプロパティに関連する演習もあります。
以下では、行列式の各プロパティを 1 つずつ説明しますが、必要に応じて、下の概要表に直接スキップできます。 😉
性質 1: 転置行列の行列式
行列の行列式は、その転置行列の行列式と同等です。
![]()
例:
![Rendered by QuickLaTeX.com \lvert A \rvert = \begin{vmatrix} 2 & 3 \\[1.1ex] 1 & 5 \end{vmatrix} = 2 \cdot 5 - 1 \cdot 3 = 10 - 3 = \bm{7}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7e39b73d52e436c660c2c9f2eeed39f6_l3.png)
次に、2×2 行列を転置し、行列式を解きます。前と同じ結果が得られることに注目してください。
![Rendered by QuickLaTeX.com \lvert A^t \rvert = \begin{vmatrix} 2 & 1 \\[1.1ex] 3 & 5 \end{vmatrix} = 2 \cdot 5 - 3 \cdot 1 = 10 - 3 = \bm{7}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc16abe425fb139cb3a6b7ba7e3b1915_l3.png)
特性 2: 行または列がゼロで埋められた行列式
行列式にゼロで埋められた行または列がある場合、行列式は 0 を返します。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} a_{11} & 0 & a_{13} \\[1.1ex] a_{21} & 0 & a_{23} \\[1.1ex] a_{31} & 0 & a_{33}\end{vmatrix}=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-54df933d2167697d926c25dd9554d90a_l3.png)
例:
![Rendered by QuickLaTeX.com \begin{vmatrix} 5 & 6 & 2 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] -3 & 1 & 4 \end{vmatrix} = \bm{0} \qquad \qquad \begin{vmatrix} 1 & -5 & 0 \\[1.1ex] 6 & 2 & 0 \\[1.1ex] 1 & 3 & 0 \end{vmatrix} = \bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-95bc2d762871764f41176acc052a633c_l3.png)
これらの例では両方とも、行列式は 0 と評価されます。最初の行列式の 2 行目はすべて 0 であり、2 番目の行列式の 3 列目もすべて 0 であるためです。
特性 3: 2 つの等しい行または列を持つ行列式
行列式に 2 つの等しい行または複数の行または 2 つの列がある場合、行列式はゼロ (0) になります。
したがって、行または列間に線形結合がある場合、つまり線形従属している場合、行列式は 0 を返します。
例:
![Rendered by QuickLaTeX.com \begin{vmatrix} 3 & 4 & 4 \\[1.1ex] -1 & 5 & 5 \\[1.1ex] 6 & 2 & 2 \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-c31b59570d4f89e8c7e7aa9f922977c5_l3.png)
この場合、列 2 と列 3 が等しいため、行列式は 0 を返します。
プロパティ 4: 行列式の行または列を変更する
2 つの行または 2 つの列が相互に変更されると、行列式は同じ結果を返しますが、符号は異なります。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} a & b & c \\[1.1ex] d & e & f \\[1.1ex] g & h & i \end{vmatrix}= - \begin{vmatrix} a & c & b \\[1.1ex] d & f & e \\[1.1ex] g & i & h \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-de79fc53e94c9a30d8a271d42d4e3494_l3.png)
例:
![Rendered by QuickLaTeX.com \begin{vmatrix} 3 & 2 & -4 \\[1.1ex] 1 & 5 & 6 \\[1.1ex] 1 & 0 & -3 \end{vmatrix} = \displaystyle -45 +12+0+20-0+6= \bm{-7}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c2e4806318fa67998b339383a9dc9ea5_l3.png)
ここで、列 2 と列 3 の順序を相互に変更します。結果は同じですが、符号が異なることに注意してください。
![Rendered by QuickLaTeX.com \begin{vmatrix} 3 & -4 & 2 \\[1.1ex] 1 & 6 & 5 \\[1.1ex] 1 & -3 & 0 \end{vmatrix} = \displaystyle 0-20-6-12+45-0= \bm{+7}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4a4de8b8cf37df2c3cce69d16a19a578_l3.png)
プロパティ 5: 行列式の行にスカラーを乗算する
行または列全体のすべての要素に実数を乗算することは、行列式の結果にその数値を乗算することと同じです。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} k \cdot a_{11} & k \cdot a_{12} & k \cdot a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix} =k \cdot \begin{vmatrix} a_{11} & a_{12} & a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-06cf5f62a3d703b43bb68b319839df26_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} k \cdot a_{11} & a_{12} & a_{13} \\[1.1ex] k \cdot a_{21} & a_{22} & a_{23} \\[1.1ex] k \cdot a_{31} & a_{32} & a_{33} \end{vmatrix} =k \cdot \begin{vmatrix} a_{11} & a_{12} & a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a7b38fe06dab0bbdbfef384b3e403fed_l3.png)
例:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 3 \\[1.1ex] 1 & 4 \end{vmatrix} = 8-3= \bm{5}](https://mathority.org/wp-content/ql-cache/quicklatex.com-92b404bb7ad8bbdd59c8c54c1619c37d_l3.png)
次に、同じ行列式を使用して、行全体に 2 を掛けます。結果は、前の行列式に 2、つまり 10 を掛けたものになることがわかります。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 \cdot 2 & 2 \cdot 3 \\[1.1ex] 1 & 4 \end{vmatrix} = \begin{vmatrix} 4 & 6 \\[1.1ex] 1 & 4 \end{vmatrix} = 16-6 =\bm{10}](https://mathority.org/wp-content/ql-cache/quicklatex.com-57ae1ba33c0d108f08ac9d0b5cb4a81b_l3.png)
特性 6: 行列積の決定因子
2 つの行列の積の行列式は、各行列の個別の行列式の積に等しくなります。
![]()
例:
行列式のこの性質を実証するために、次の 2 つの行列の乗算の行列式を 2 つの可能な方法で計算します。
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix}\quad B=\begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-38de0ca99ad15f40bd94f653cffacf8d_l3.png)
まず 2 つの行列を乗算し、次に結果の行列の行列式を計算します。
![Rendered by QuickLaTeX.com \displaystyle \left| A \cdot B \right| =\left| \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix} \cdot \begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}\right| = \left| \begin{pmatrix} 7 & -1 \\[1.1ex] 13 & -1 \end{pmatrix} \right| = -7 - (-13) = \bm{6}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2ad18d1637b581038b7866030d6ac9a0_l3.png)
ここで、各行列の行列式を個別に計算し、結果を乗算します。
![Rendered by QuickLaTeX.com \displaystyle \lvert A \rvert \cdot \lvert B \rvert = \left| \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}\right| = -1\cdot (-6)= \bm{6}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5f7c97d5a832d3985bf1d5e9d4d44401_l3.png)
ご覧のとおり、最初に行列の積を実行してから行列式を実行すると、最初に各行列の行列式を実行してからその結果を乗算するのと同じ結果が得られます。
一方、この条件は加算および減算演算には当てはまりません。つまり、2 つの行列の加算 (または減算) の行列式は、行列式の加算 (または減算) と同じ結果を与えません。 2 つの行列を別々に処理します。
性質 7: 逆行列の行列式
行列が可逆である場合、その逆行列の行列式は元の行列の行列式の逆行列に対応します。
![]()
例:
最初に逆行列を計算し、次にその行列式を解くことによって、この特性を検証します。結果は、元の行列の行列式を見つけてそれを反転することと同じであることがわかります。
したがって、次の行列を逆行列にして、その行列式を計算します。
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} 4 & 2 \\[1.1ex] 7 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2c77c10006d35ebc5273553fb84356e3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^{-1}= \begin{pmatrix} 2 & -1 \\[1.1ex] -\frac{7}{2} & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8a9315a8add365cd5f077c52476a827d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A^{-1} \end{vmatrix}= \begin{vmatrix} 2 & -1 \\[1.1ex] -\frac{7}{2} & 2 \end{vmatrix} = 4-\cfrac{7}{2} =\cfrac{8}{2}-\cfrac{7}{2} = \cfrac{\bm{1}}{\bm{2}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a10c873ff6c101cd2b239388393c268b_l3.png)
そして今、元の行列の行列式を解き、その逆行列を計算します。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A\end{vmatrix}= \begin{pmatrix} 4 & 2 \\[1.1ex] 7 & 4 \end{pmatrix}=16-14=2](https://mathority.org/wp-content/ql-cache/quicklatex.com-850e5404f5352782327918caab3e1440_l3.png)
![]()
ご覧のとおり、両方の操作の結果は同じです。したがって、その性質は証明されます。
プロパティ 8: 決定子の行を置換する
行列式の行は、同じ行に数値を乗算した別の行を加算 (または減算) することによって置き換えることができます。
例:
次の例では、このプロパティを確認します。まず行列式を計算し、次に行列式の行を演算してその結果を再計算します。どちらの場合でも同じ結果が得られることがわかります。
そこで、まず、Sarrus ルールを使用して 3×3 行列式を計算してみましょう。
![Rendered by QuickLaTeX.com \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 3 & 0 & 1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} \displaystyle=0+0+9-0+6-18 = \bm{-3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4ccd76fc3a2b7cd7afc7d8f9de8ffde1_l3.png)
次に、 2 行目に、2 を乗算した最初の行を追加します。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 3 & 0 & 1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} \begin{matrix} \\[1.1ex] \xrightarrow{f_2 + 2f_1} \\[1.1ex] \ \end{matrix} \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 7 & 2 & -1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4bc2e6bd78446fb68f29b4a5503a6828_l3.png)
そして、行の 1 つを変換した後、行列式を解きます。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 7 & 2 & -1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} = 24+0+21-0-6-42=\bm{-3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-045eb6f32420fbbf538a9e0a540ce119_l3.png)
どちらの場合も結果は -3 でした。したがって、行が同じ行と別の行の合計に数値を乗じたものに置き換えられても、行列式の結果は変わらないことが示されています。
性質 9: 三角行列の行列式
三角行列の行列式は、その主対角要素の積です。
例:
例として、次の三角行列の行列式を解きます。
![Rendered by QuickLaTeX.com \begin{vmatrix} 2 & 3 & 5 \\[1.1ex] 0 & -1 & 7 \\[1.1ex] 0 & 0 & 4 \end{vmatrix} \displaystyle= 2 \cdot (-1) \cdot 4 = \bm{-8}](https://mathority.org/wp-content/ql-cache/quicklatex.com-40ebfa5f9f06e63ad1325d9331a57bde_l3.png)
性質 10: 対角行列の行列式
対角行列の行列式は、主対角要素の乗算に等しい。
例:
例として、次の対角行列の行列式を考えてみましょう。
![Rendered by QuickLaTeX.com \begin{vmatrix}5 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & -2 \end{vmatrix} \displaystyle= 5 \cdot 3 \cdot (-2) = \bm{-30}](https://mathority.org/wp-content/ql-cache/quicklatex.com-56e1b3093685a1af729310752b03dfc9_l3.png)
行列式の性質の概要表
説明した行列式の特性は、次の表に要約できます。
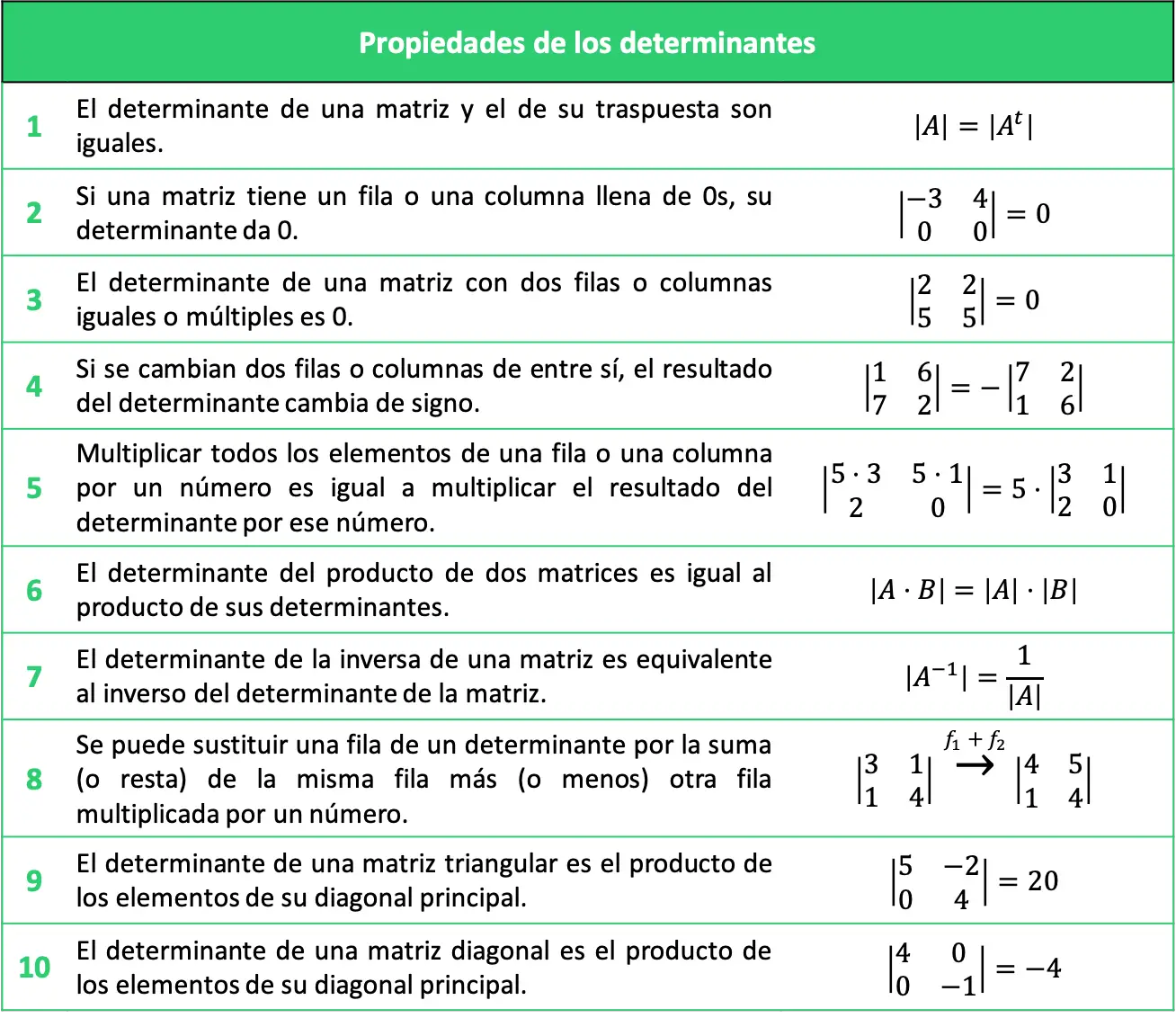
行列式の特性を使った演習問題を解く
演習 1
次の行列式を解きます。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & 1 & 0 \\[1.1ex] 4 & 2 & 0 \\[1.1ex] -1 & 6 & 0 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-97dfc1ebfc5db73750870911108bd447_l3.png)
行列式の行または列がゼロで埋められている場合、行列式は 0 を返します (プロパティ 2)。したがって、 3 列目はゼロで埋められるため、行列式の結果は 0 になります。
演習 2
次の行列式を解きます。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 4 & 2 & -3 & 5 \\[1.1ex] 1 & 5 & 3 & 2 \\[1.1ex]4 & 2 & -3 & 5 \\[1.1ex] -2 & 0 & 4 & 3 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bdb315ba588fe5fdfb03c7fea2857b16_l3.png)
行列式に 2 つの等しい行または複数の行または 2 つの列がある場合、行列式は 0 (プロパティ 3) を返します。したがって、 1 行目と 3 行目は等しいため、行列式の結果は 0 になります。
演習 3
次の行列式を計算します。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & 0 & 2 & 2 \\[1.1ex] 3 & 1 & 5 & 6 \\[1.1ex] 1 & 3 & -2 & 2 \\[1.1ex] 2 & 2 & 0 & 4 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96c5cfee4c4189e49b54fdf43b2a0457_l3.png)
行列式に 2 つの等しい行または複数の行または 2 つの列がある場合、行列式は 0 (プロパティ 3) を返します。したがって、 4 列目は 1 列目の 2 倍であるため、行列式の結果は 0 になります。
演習 4
行列の要素はわかりませんが、行列式の結果はわかります。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix} = 3](https://mathority.org/wp-content/ql-cache/quicklatex.com-e20d9016edd52f18d3ffc928d2658efe_l3.png)
前の行列式の結果と行列式のプロパティから、次の行列式の結果を計算します。
![Rendered by QuickLaTeX.com \displaystyle \mathbf{a} \bm{)} \ \begin{vmatrix} a & c \\[1.1ex] b & d \end{vmatrix} \qquad \mathbf{b} \bm{)} \ \begin{vmatrix} b & a \\[1.1ex] d & c \end{vmatrix} \qquad \mathbf{c} \bm{)} \ \begin{vmatrix} a & 3b \\[1.1ex] c & 3d \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9c20de8d82171dc8fb784e2549521f37_l3.png)
のために)
![]()
の転置行列です
![]()
。そして、行列の行列式は、その転置行列の行列式と等しくなります (性質 1)。したがって、この行列式の結果も 3 になります。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} a & c \\[1.1ex] b & d \end{vmatrix}=\begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix}=\bm{3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5bf7ae0a2ff32d75a6f7abafb623639c_l3.png)
b)決定において
![]()
列 1 と列 2 はステートメントの決定子に関して変更されています
![]()
。したがって、プロパティ 4 によれば、結果はステートメントの決定子の結果と同じですが、符号が異なります (つまり、-3)。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} b & a \\[1.1ex] d & c \end{vmatrix} = - \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix}= \bm{-3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d6d14aa2f6b8c7d1fd064daef8dd0eec_l3.png)
c)決定において
![]()
ステートメントの行列式の 2 番目の列全体が 3 で乗算されています。したがって、プロパティ 5 から、その結果はステートメントの行列式に 3 を掛けた結果、つまり 9 になると推測できます。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} a & 3b \\[1.1ex] c & 3d \end{vmatrix} =3 \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix} =3 \cdot 3 = \bm{9}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b1a7ffec429367a2fd967a197d0299d2_l3.png)
演習 5
これら 2 つの決定要因の結果はわかっています。
![Rendered by QuickLaTeX.com \displaystyle\vert A \vert = \begin{vmatrix} 1 & 2 & 0 & 1 \\[1.1ex] -2 & -1 & 1 & 0 \\[1.1ex] 1 & 3 & 3 & -1 \\[1.1ex] 3 & 4 & 1 & 1 \end{vmatrix}=8](https://mathority.org/wp-content/ql-cache/quicklatex.com-e938c40ce401263da9835fa77fc9a1dd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle\vert B \vert = \begin{vmatrix} 0 & 1 & 3 & 2 \\[1.1ex] -1 & -2 & 0 & 0 \\[1.1ex] 3 & 1 & 1 & 2 \\[1.1ex] -1 & 2 & 3 & 1 \end{vmatrix} = - 4](https://mathority.org/wp-content/ql-cache/quicklatex.com-6cea0d73e66099f2a10f71f7267baee9_l3.png)
この情報から、次のように計算します。
![]()
行列式の結果を計算するために、4×4 行列を乗算する必要はありません。 2 つの行列の積の行列式は、各行列の行列式の積に個別に等しいため(プロパティ 6)。まだ:
![]()