この記事では、アフィン関数と線形関数の説明と、これら 2 種類の関数の違いについて説明します。さらに、アフィン関数と線形関数をグラフ化する方法と、2 点からそれらの式を計算する方法の例も示します。最後に、いくつかの演習を段階的に解決してトレーニングできるようになります。
アフィン関数と線形関数とは何ですか?
アフィン関数と線形関数の定義は次のとおりです。
アフィン関数は 1 次多項式関数、つまりグラフ上で表現される関数です。関連する機能は次のとおりです。
![]()
金
![]()
は線の傾きであり、
![]()
これは y 切片、つまり関数が垂直軸と交差する場所です。
数学では、アフィン関数は線形代数の文脈では線形変換とも呼ばれます。
線形関数は、独立した項を持たないアフィン関数です。したがって、一次関数の公式は次のようになります。
![]()
金
![]()
線の傾きです。
線形関数とアフィン関数の定義域と範囲 (または範囲) はすべて実数です。
![]()
![]()
線形関数とアフィン関数の違いは何ですか?
線形関数とアフィン関数の概念を見てきましたが、それらが互いに非常に似ていることに気づいたでしょう。ただし、次のような両者の違いは非常に重要です。
線形関数とアフィン関数の唯一の違いは、線形関数には独立した項がないのに対し、アフィン関数には常にゼロ (0) とは異なる切片 (n) の係数があることです。
一次関数
![]()
一次関数
![]()
これは、線形関数が常に座標原点、つまり点 (0,0) を通過することを意味します。一方、アフィン関数は 0 以外の切片を持つため、この点を通過することはありません。
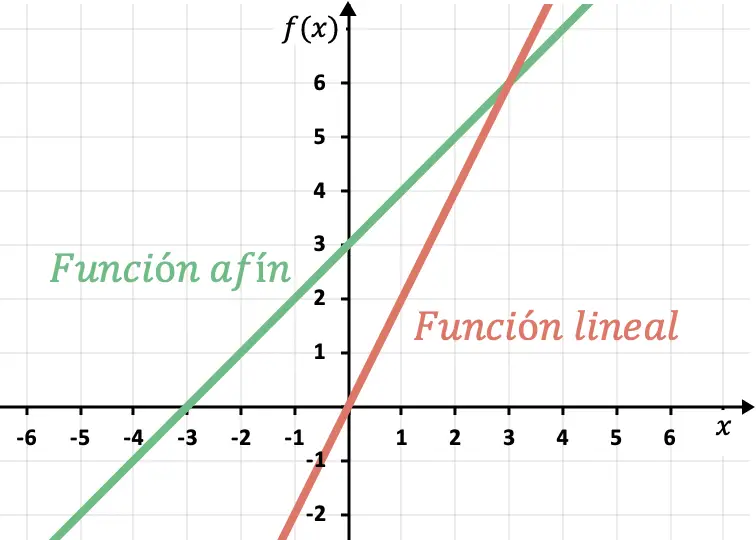
線形関数またはアフィン関数の傾きと y 切片
このセクションでは、アフィン関数または線形関数の例を分析して、用語の意味を理解します。
![]()
そして
![]()
、言い換えれば、傾きと y 切片です。
- グラフに表示された関数の式を決定し、それを線形関数またはアフィン関数として分類します。
これらのタイプの関数は次の式に従います。
![]()
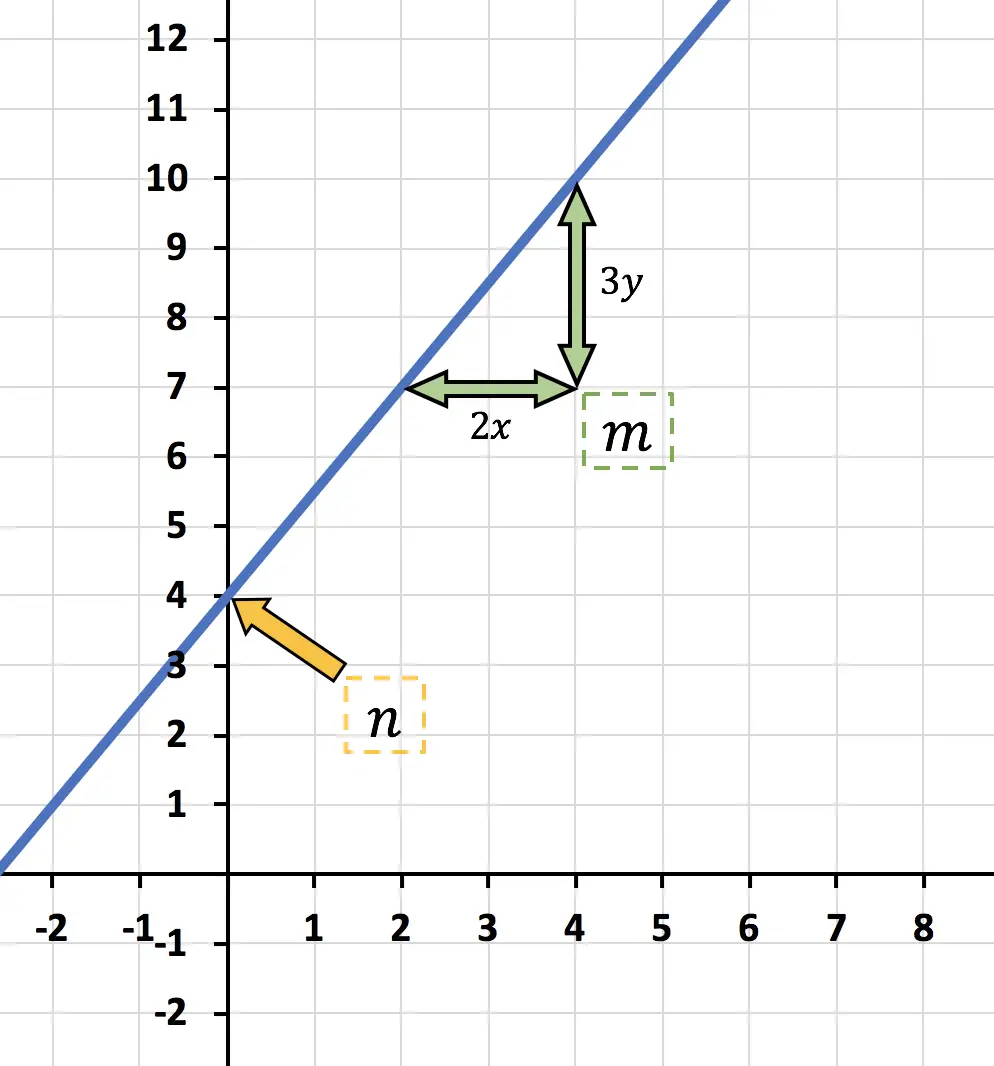
![]()
これは y 切片、つまり関数が垂直 Y 軸と交差する場所です。したがって、この場合は次のようになります。
![]()
別の側面では、
![]()
線の傾きです。 Y は、2 点間のyの差をこれらの同じ 2 点間のxの差で割ることによって計算できます。
![]()
![]()
これは、「x ごとに y がどれだけ増加するか」を示しているため、この場合、関数「2x ごとに 3y が増加する」になります。
結論として、グラフで表されるアフィン関数の式は次のようになります。
![]()
さらに、y 切片はゼロではないため、アフィン関数になります。
以下に、理解を深めていただくために、線形関数とアフィン関数の例をさらに示します。
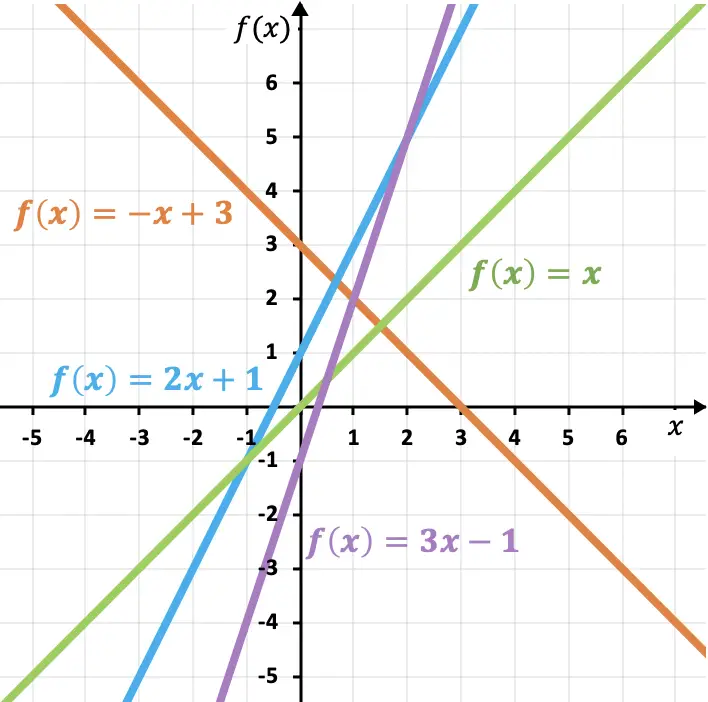
これらの例からわかるように、傾きが大きいほど線の急勾配が高くなり、したがって関数が大きくなります。同様に、傾き係数は関数の増加または減少を決定します。
- 傾きが正の場合、関数は増加しています。つまり、 xが増加するにつれて関数も増加します。
- 傾きが負の場合、関数は減少しています。つまり、 xが増加するにつれて関数は減少します。
さらに、2 本の線が平行か垂直かをその傾きによって判断することもできます。
- 2 本の線の傾きが同じ場合、それらは平行です。つまり、どの点でも交差していないか、完全に同一です。
![]()
- 一方、2 本の線は垂直です。つまり、それらの傾きが次の関係に対応する場合、それらは垂直角 (90 度) で交差します。
![]()
アフィン関数または線形関数の表現例
例を使用して 1 次関数をグラフ化する方法を見てみましょう。
- 次のアフィン関数をグラフ化します。
![]()
最初に行う必要があるのは、値の配列を作成することです。これを行うには、必要な値を付与します
![]()
の値を取得するには
![]()
:
![]()
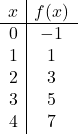
2 つのポイントを含む値の表で十分ですが、それが正しいことを確認するためにさらに多くのポイントを実行できます。
値のテーブルを作成したら、グラフ上に点をプロットします。
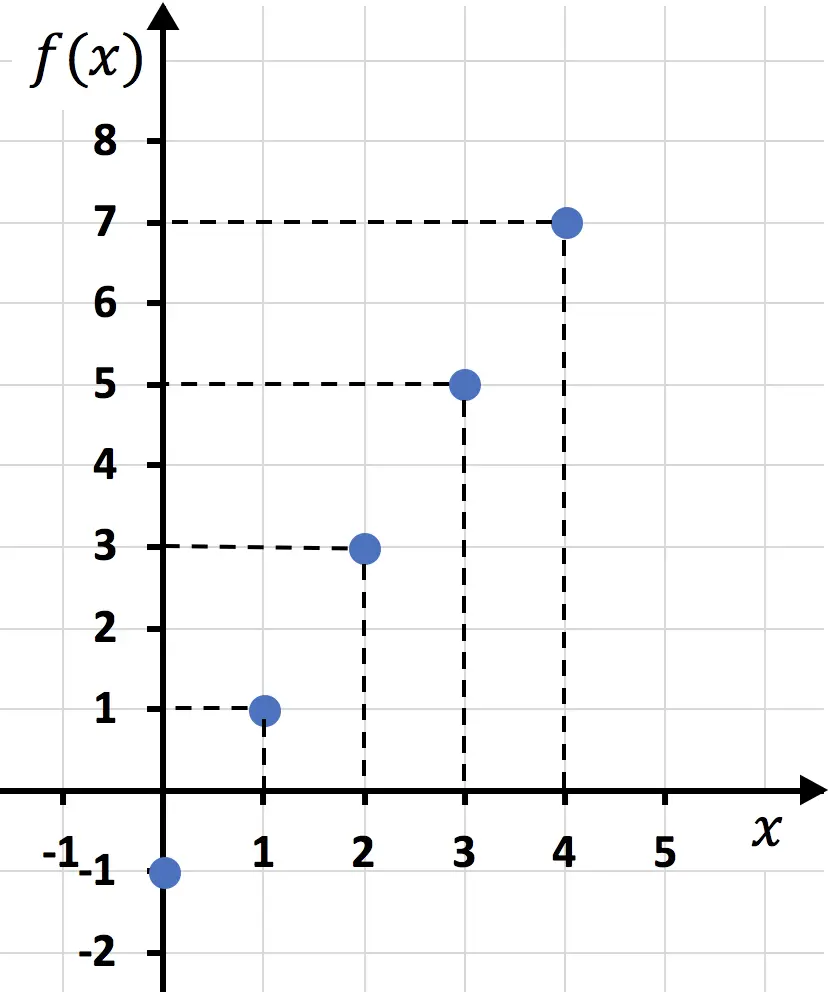
最後に、点を結合して線を描きます。
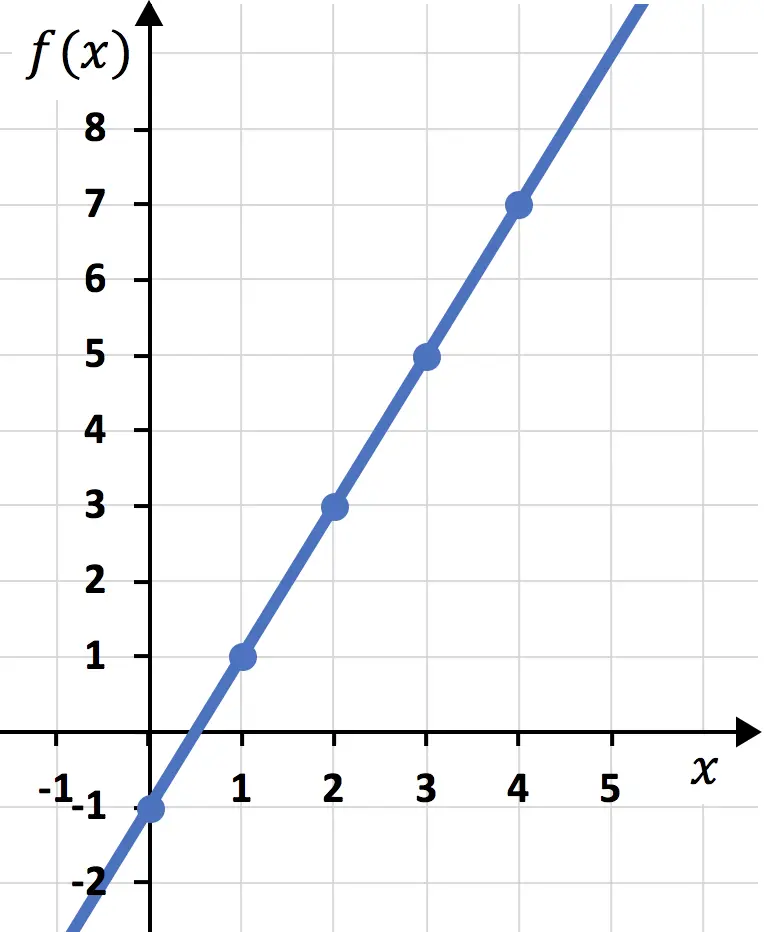
このようにして、関数をグラフ上に表現することができました。 ご覧のとおり、これは複雑ではありません。最初に値の表を作成し、それからグラフ上に点をプロットするだけです。
2 点から線形関数またはアフィン関数を計算する方法
次に、例を使用して 2 つの点から線形関数またはアフィン関数を見つける方法を見てみましょう。
- を満たす一次関数を計算します。
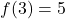
そしてポイントを通過します
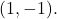
初めに、
![]()
これは、関数が点を通過することを意味します
![]()
。
したがって、関数が通過する 2 つの点があるため、傾きを計算できます。
![]()
関数:
2つの点を考慮すると、
![]()
そして
![]()
、 スロープ
![]()
関数の計算は次のようになります。
![]()
私たちの場合、関数はポイントを通過します。
![]()
そして
![]()
。それで斜面は
![]()
関数の内容は次のとおりです。
![]()
したがって、関数は次の形式になります。
![]()
わかったら
![]()
私たちはその謎を解くことができます
![]()
。これを行うには、関数に属する点の座標を方程式に代入します。たとえば、ポイント (3.5):
![]()
結果として得られる方程式を解きます。
![]()
![]()
![]()
![]()
したがって、一次関数は次のようになります。
![]()
線形関数とアフィン関数に関する演習を解決しました
演習 1
次のアフィン関数の傾きと原点を決定します。
![]()
一次関数の形式は次のとおりです。
![]()
したがって、関数の傾きはxに付随する数値であり、この場合は -5 です。
![]()
そして、y 切片は独立項であり、この場合は -2 です。
![]()
演習 2
次のアフィン関数をグラフ化します。
![]()
まず値を与えます
![]()
値のテーブルを作成するには:
![]()
![]()
![]()
![]()
![]()
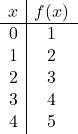
次に、値の表からの点をグラフ上に表し、線を描きます。

演習 3
次のアフィン関数をグラフにプロットします。
![]()
まず値を与えます
![]()
値のテーブルを作成するには:
![]()
![]()
![]()
![]()
![]()
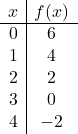
そして最後に、グラフ上の値の表の点を表し、線を描きます。
演習 4
点 (2,3) と (0,1) を通過するアフィン関数の式を見つけます。
関数は点 (2,3) と (0,1) を通過するため、関数の傾きは次のようになります。
![]()
そして関数は次のような形式になります。
![]()
m がわかったら、 nを計算できます。これを行うには、関数に属する点の座標を方程式に代入する必要があります。たとえば、ポイント (2,3):
![]()
![]()
次に、結果として得られる方程式を解く必要があります。
![]()
![]()
したがって、関数は次の式に対応します。
![]()
演習 5
次のアフィン関数をグラフ化します。
![]()
まず値を与えます
![]()
値のテーブルを作成するには:
![]()
![]()
![]()
![]()
![]()

次に、値の表からの点をグラフ上に表し、線を描きます。

演習 6
次の 2 つの条件を満たす一次関数を計算します。
![Rendered by QuickLaTeX.com \begin{array}{c}f(3) =-2 \\[3ex] f(-1)=6 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a3d1692f49f622f3167c7b58da6553eb_l3.png)
それが叶いますように
![]()
これは、関数が点 (3,-2) を通過することを意味します。そして、同じように、
![]()
これは、関数が点 (-1.6) を通過することを意味します。
したがって、関数は点 (3,-2) と (-1,6) を通過するため、その傾きは次のようになります。
![]()
したがって、関数は次の形式になります。
![]()
m がわかれば、 nを計算できます。これを行うには、関数に属する点の座標を方程式に代入します。たとえば、点 (3,-2) は次のようになります。
![]()
そして、結果として得られる方程式を解きます。
![]()
![]()
![]()
したがって、関数は次のようになります。
![]()
演習 7
実行するアフィン関数を見つけます
![]()
そして点(3.5)を通過します。
それが叶いますように
![]()
これは、関数が点 (1,6) を通過することを意味します。
したがって、関数は点 (1.6) と (3.5) を通過するため、その傾きは次のようになります。
![]()
したがって、関数は次の形式になります。
![]()
項mがわかれば、係数nを計算できます。これを行うには、関数に属する点の座標を方程式に代入します。たとえば、点 (1,6) は次のようになります。
![]()
結果として得られる方程式を解きます。
![]()
![]()
分数を加算するには、まず分数を公分母に減らしてから、分子を加算する必要があることに注意してください。
![]()
![]()
![]()
したがって、関数は次のようになります。
![]()
演習 8
線形関数とアフィン関数に関連する次の問題を解きます。
店舗では、価格が 1 個あたり 15 ユーロの場合は製品を 40 個販売し、価格が 1 個あたり ユーロの場合は 65 個販売します。
- 製品の需要関数を、アフィン関数であると仮定して計算します。
- 価格を 1 ユニットあたり 12 ユーロに設定した場合、何ユニット販売されますか?
アフィン関数なので、関数の型は次のようになります。
![]()
金
![]()
商品の単価となりますが、
![]()
販売単位となります。
プレスリリースによると、価格が 1 台あたり 15 ユーロの場合、40 台が販売されます。したがって、
![]()
価格と
![]()
販売されたユニットの数に応じて、次の平等が尊重される必要があります。
![]()
価格が 1 台あたり 10 ユーロの場合、65 台が販売されます。したがって、同じ推論を使用すると、次のようになります。
![]()
それが叶いますように
![]()
これは、関数が点 (15.40) を通過することを意味します。そして
![]()
これは、関数が点 (10.65) を通過することを意味します。
したがって、関数の傾きは次のようになります。
![]()
したがって、関数は次の形式になります。
![]()
m がわかったら、 nを計算できます。これを行うには、関数に属する点の座標を方程式に代入します。たとえば、ポイント (午後 3 時 40 分):
![]()
そして、結果として得られる方程式を解きます。
![]()
![]()
![]()
したがって、売上高を価格に結び付ける関数は次のようになります。
![]()
一方、関数では
![]()
価格を表します。したがって、価格が 1 ユニットあたり 12 ユーロの場合に販売されるユニット数を知るには、次のように計算する必要があります。
![]()
![]()
![]()
![]()
したがって、価格が 12 ユーロ/ユニットの場合、55 ユニットが販売されることになります。