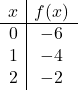このページでは絶対値関数とは何かについて説明します。また、区分絶対値関数を定義する方法と、これらのタイプの関数をグラフ上で表現する方法も学習します。さらに、絶対値関数の例も示し、演習や問題を段階的に解いて練習することができます。
絶対値関数とは何ですか?
絶対値関数の定義は次のとおりです。
関数の絶対値は、そのすべてのイメージをポジティブ イメージに変換します。したがって、絶対関数のパスは負の値を持つことはできません。
次の関数は絶対値関数の例です。
![]()
ある時点で関数を評価したときに肯定的な結果が得られた場合、その結果は肯定的なままになります。
![]()
一方、結果が負の場合は正になります。
![]()
絶対値関数はその特性から理解するのが少し難しいため、通常は高校で教えられます。
絶対値を使用して関数を区分的に定義する方法
絶対値関数は区分関数として表現できます。これを行うには、関数の符号を負の間隔で変更する必要があります。
絶対値関数から区分関数に移行する方法の例を見てみましょう。
- 次の関数を区分関数として絶対値で表します。
![]()
最初に行う必要があるのは、関数がいつ負になるかを判断することです。これを行うには、代数式の絶対値を 0 に設定し、方程式を解きます。
![]()
![]()
![]()
![]()
![]()
取得した値を次の行で表します。
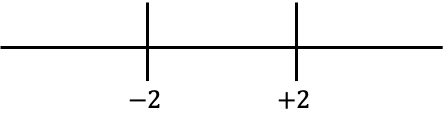
そして、線の各区間で絶対値を使わずにどの符号が関数を持っているかを調べます。
![]()
たとえば、-2 より小さい点はすべて考慮されます。
![]()
![]()
![]()
ネガティブ
![]()
たとえば、-2 から +2 までの任意の点を取得します。
![]()
![]()
![]()
ポジティブ
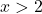
![]()
![]()
![]()
ネガティブ

これまで見てきたように、絶対値のない関数は区間上で負になります。
![]()
そして

![\displaystyle f(x)= \lvert 4 - x^2 \rvert = \left\{ \begin{array}{lcl} -(4-x^2) & \text{si} & x<-2 \\[2ex] 4-x^2 & \text{si} & -2 \le x \le 2 \\[2ex] -(4-x^2) & \text{si} & x>2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”372″ style=”vertical-align: 0px;”></p>
</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5f441ea5792fb5cc7ba8300f71defef_l3.png)
![\displaystyle f(x)= \lvert 4 - x^2 \rvert = \left\{ \begin{array}{lcl} -4+x^2 & \text{si} & x<-2 \\[2ex] 4-x^2 & \text{si} & -2 \le x \le 2 \\[2ex] -4+x^2 & \text{si} & x>2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”358″ style=”vertical-align: 0px;”></p>
</p>
<p>一部の間隔では等価性を含める必要があることに注意してください。たとえば、ここでは 2 番目の間隔に置きます。</p>
</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-89ab8a514afe36c94d7072efe47ef507_l3.png)
![]()
。ただし、すべての重要なポイントが同点である限り、任意の間隔に配置できます。つまり、次のように関数を定義しても同じになります。
![Rendered by QuickLaTeX.com \displaystyle f(x)= \lvert 4 - x^2 \rvert = \left\{ \begin{array}{lcl} -4+x^2 & \text{si} & x\le-2 \\[2ex] 4-x^2 & \text{si} & -2 < x < 2 \\[2ex] -4+x^2 & \text{si} & x\ge 2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-5cce3bcc22edb3a7f511cea0a1c32372_l3.png)
関数を絶対値で表す方法
グラフ上で関数を絶対値で表すには、以下で説明する手順に従う必要があります。
- 絶対値を持たないかのように関数を表現します。
- 関数が負の区間、つまり X 軸の下にある区間では、対称関数を描画します。
- X 軸の下にある関数の部分を削除します。
絶対値を使用して関数をグラフ化する方法の例を見てみましょう
- 次の関数を絶対値でグラフ化します。
![]()
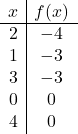
絶対値を使用して関数を表現するには、まず絶対値を使用せずに関数を表現する必要があります。したがって、絶対値を含まない関数値の表を作成します。
![]()
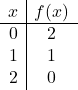
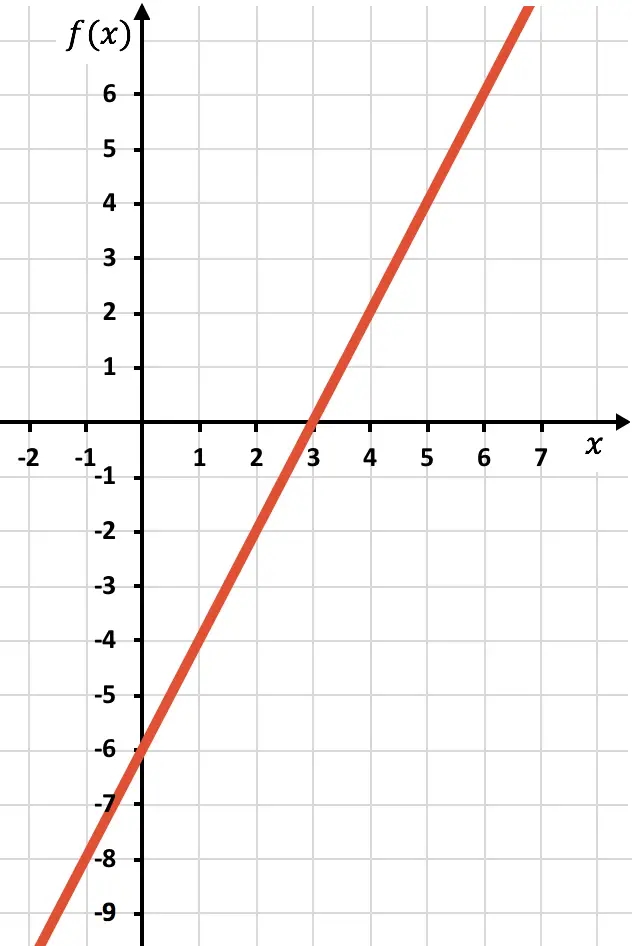
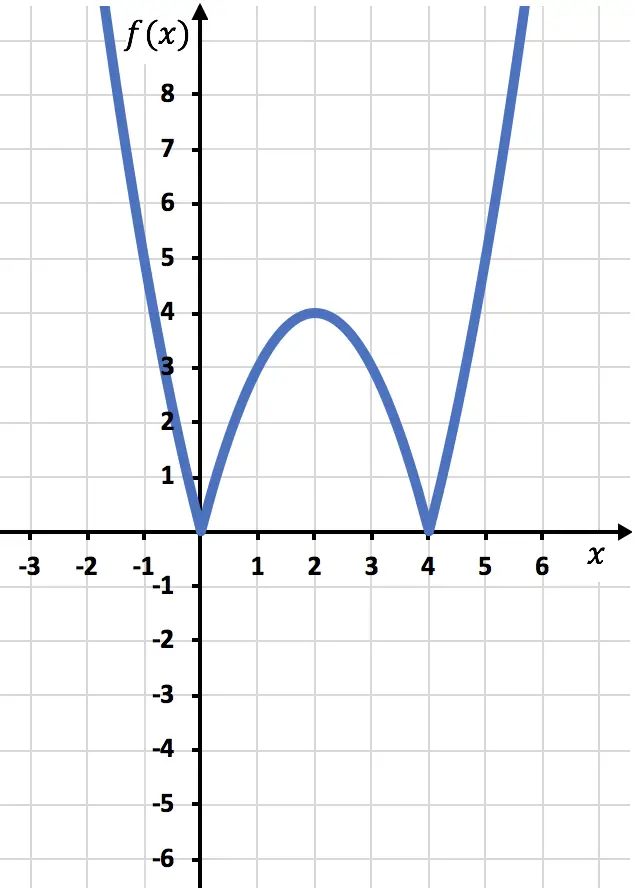
通常の関数であるかのように点をグラフ化し、線を描きます。
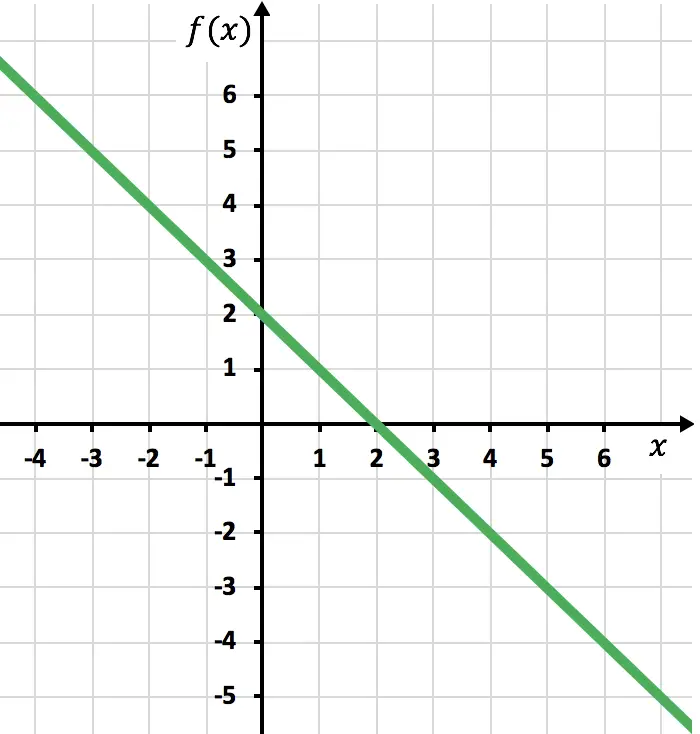
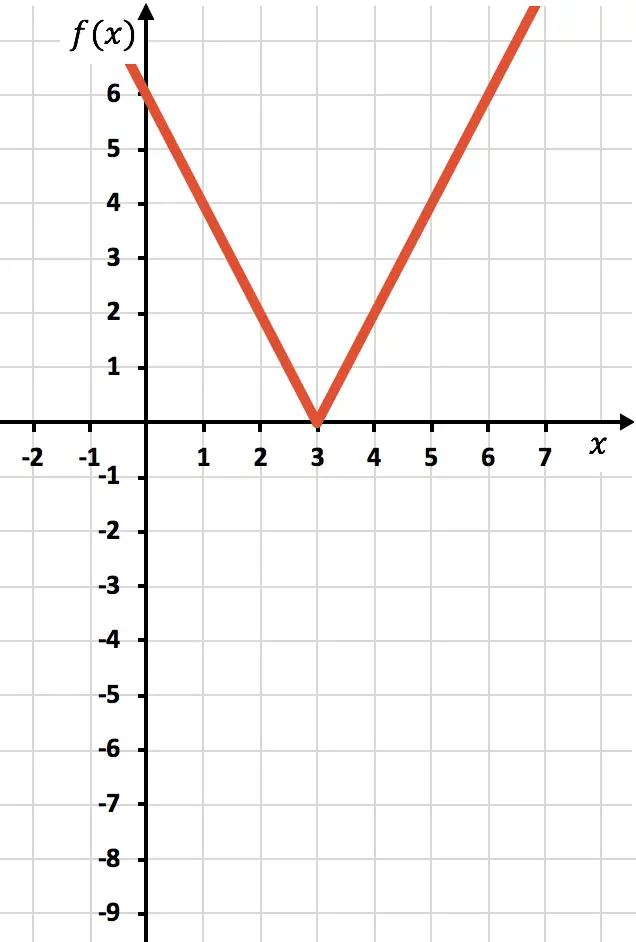
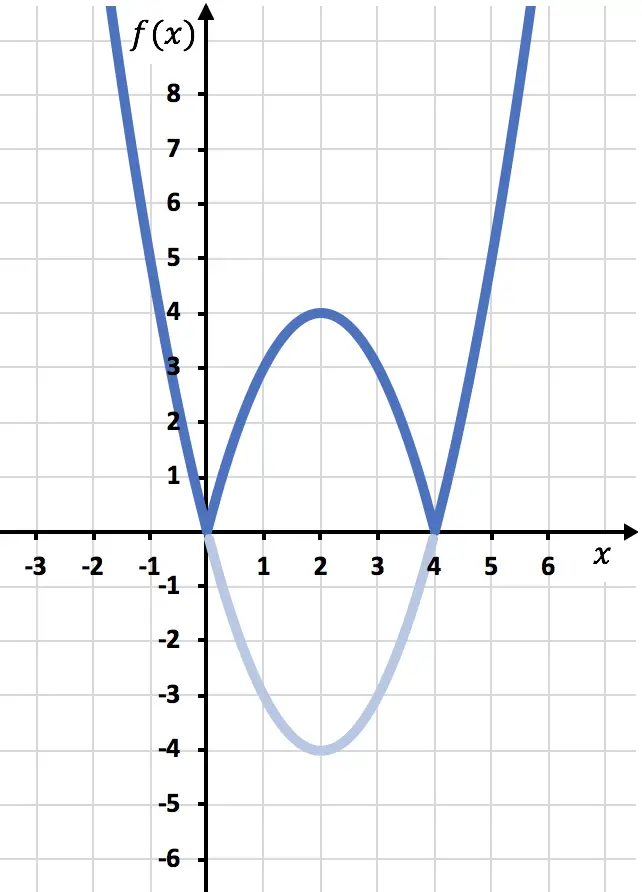
次に、関数が負の位置、つまり x 軸の下にある対称関数を描画する必要があります。したがって、x=2 から関数を逆にします。
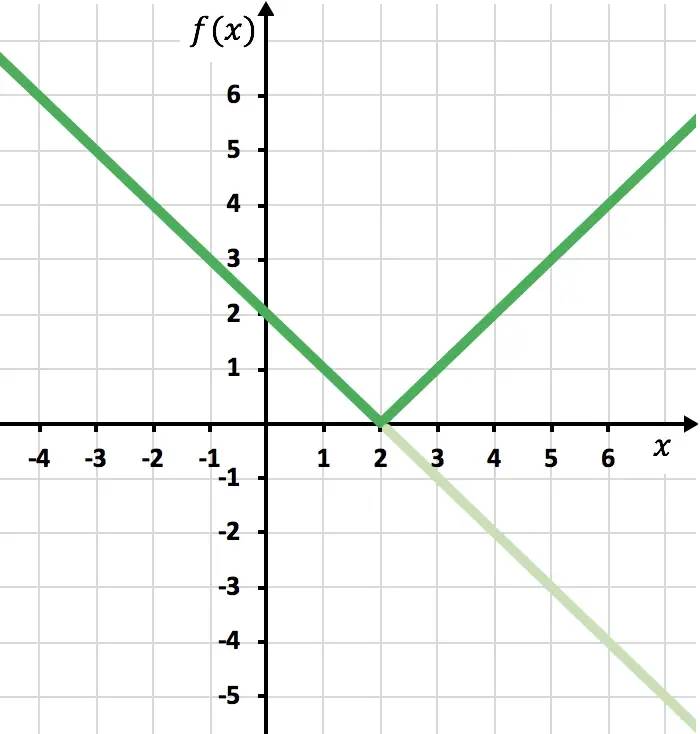
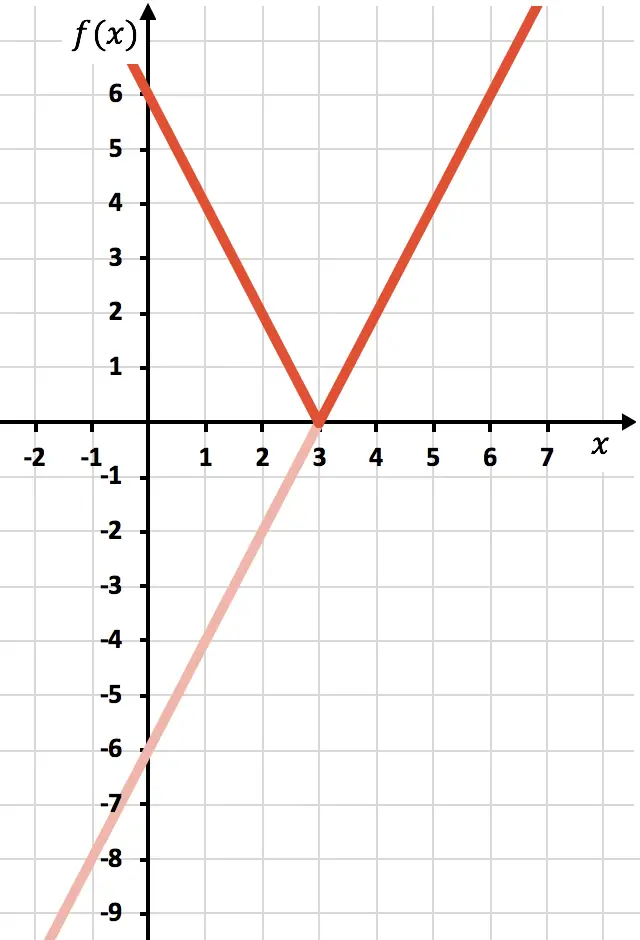
最後に、X 軸の下にある関数のトレースを削除します。

このようにして、関数を絶対値で表現しました。ご覧のとおり、唯一の変更点は、OX 軸の下にある関数の部分を反転する必要があることです。したがって、絶対値を持つ関数のグラフは常に正の半 Y 軸の側にあります。
一方、概念を復習すると、グラフから、前の絶対値関数の領域は完全に実数で構成されていることが推測できます。一方、絶対値を伴う前記関数の範囲は、正の数とゼロのみで構成されます。
絶対値関数に関する演習を解決しました
演習 1
次の関数を区分関数として絶対値で表します。
![]()
まず第一に、関数が負の場合を確認する必要があります。これを行うには、絶対値をゼロに設定し、方程式を解きます。
![]()
![]()
次の行で見つかった値を表します。
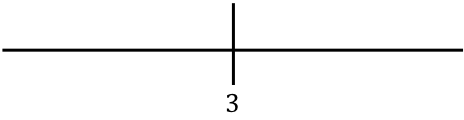
ここで、絶対値を使用せずに関数の各区間の点を評価して、関数が線の各セクションで実際にどのような符号を持っているかを確認します。
![]()
たとえば、3 未満の任意の点を取得します。
![]()
![]()
![]()
ポジティブ
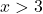 たとえば、3 より大きい任意の点を取得します。
たとえば、3 より大きい任意の点を取得します。
![]()
![]()
![]()
ネガティブ
絶対値のない関数は、区間 x>3 では負になります。したがって、この区間で符号を変更して関数をダッシュで表現する必要があります。
![Rendered by QuickLaTeX.com \displaystyle f(x)= \lvert -x+3 \rvert = \left\{ \begin{array}{lcl} -x+3 & \text{si} & x<3 \\[2ex] -(-x+3) & \text{si} & x\ge 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-f7cfaaff9890b356f1db6805ed94dbb8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle f(x)= \lvert -x+3 \rvert = \left\{ \begin{array}{lcl} -x+3 & \text{si} & x<3 \\[2ex] x-3 & \text{si} & x\ge 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-d249715b500ad03c44ab6ab5838e32e8_l3.png)
演習 2
絶対値を使用して次の関数の区分式を求めます。
![]()
最初に行う必要があるのは、関数がいつ負になるかを判断することです。これを行うには、絶対値引数をゼロに設定し、方程式を解く必要があります。
![]()
![]()
![]()
![]()
![]()
右側で得られた関数の根を表します。
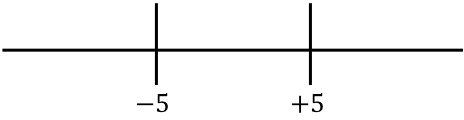
そして、線の各区間で絶対値を使わずにどの符号が関数を持っているかを調べます。
![]()
たとえば、-5 未満の任意の点を取得します。
![]()
![]()
![]()
![]()
ポジティブ
![]()
たとえば、-5 から +5 までの任意の点を取得します。
![]()
![]()
![]()
![]()
ネガティブ
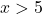 たとえば、5 より大きい任意の点を取得します。
たとえば、5 より大きい任意の点を取得します。
![]()
![]()
![]()
![]()
ポジティブ

したがって、絶対値のない関数は、-5<x<5 の区間でのみ負になります。したがって、この区間の符号のみを変更して関数を部分的に表現する必要があります。
![\displaystyle f(x)= \lvert 3x^2-75 \rvert = \left\{ \begin{array}{lcl} 3x^2-75 & \text{si} & x<-5 \\[2ex] -(3x^2-75) & \text{si} & -5 \le x \le 5 \\[2ex] 3x^2-75 & \text{si} & x>5 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”408″ style=”vertical-align: 0px;”></p>
</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e0fad2e3a9e1a6d1edcde507e60230b_l3.png)
![\displaystyle f(x)= \lvert 3x^2-75 \rvert = \left\{ \begin{array}{lcl} 3x^2-75 & \text{si} & x<-5 \\[2ex] -3x^2+75 & \text{si} & -5 \le x \le 5 \\[2ex] 3x^2-75 & \text{si} & x>5 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”394″ style=”vertical-align: 0px;”></p>
</p>
<div class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-5f9638fe87ad09d7dbcdb8e30a16688f_l3.png)