このページでは、組み合わせ数とは何か、その計算方法(公式)について説明します。さらに、任意の組み合わせ数の計算方法の例を確認し、段階的に解決される演習で練習することができます。また、組み合わせ数のすべての特性と応用も示します。そして最後に、計算機を使って直接、組み合わせ数値の結果を求める方法を学びます。
組み合わせ数とは何ですか?
数学では、二項係数とも呼ばれる組み合わせ数 は、n 個の要素のセットから形成できる k 個の要素のグループの通常の組み合わせ (繰り返しのない組み合わせ) の数です (n>k)。
組み合わせ番号は次のように括弧内に表されます。
![]()
一方、組み合わせ数はkよりもnと読み取られます。同様に、 nは分子と呼ばれ、 kは次数と呼ばれます。
組み合わせ数の定義だけでは、その意味を理解するのは難しいです。ただし、ここでは、組み合わせ数が数学的にどのように決定されるかを見てから、この組み合わせ論の概念をさらに深く掘り下げていきます。そうすることでよりよく理解できることがわかります。
組み合わせ数の公式
組み合わせ数 (または二項係数) の値を計算する式は次のとおりです。
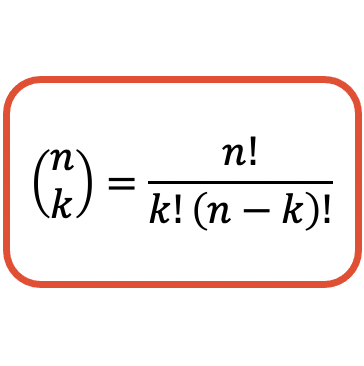
代数学では、感嘆符は数値の階乗に対応することを思い出してください。数値の階乗を求めるには、1 のすべての正の整数にその数値を掛ける必要があります。たとえば、数値 4 の階乗を計算するには、1、2、3、4 を乗算する必要があります。
![]()
0 の階乗は 1 に等しいことを知っておくことも重要です。
![]()
組み合わせ数の計算例
次に、例として組み合わせ数値の値を段階的に決定します。その方法を確認してください。
- 3 に対する組み合わせ数 5 の値を計算します。
5 対 3 の二項係数は、次の式に対応します。
![]()
したがって、組み合わせ数値の公式を適用する場合、その値を決定するには、次の操作を実行する必要があります。
![]()
または同等のもの:
![]()
したがって、階乗を求めます。
![]()
乗算 1・2・3 は分子と分母で繰り返されるため、この係数を削除すると分数を簡略化できます。
![]()
![]()
ここで積を計算します。
![]()
そして最後に、次のように分割します。
![]()
組み合わせ数の性質
組み合わせ数、つまり二項係数は、次のプロパティに従って組み合わせることができます。
- 2 つの相補的な組み合わせ数は、同じ分子nを持ち、それらの次数の和がその分子に等しい数です。したがって、2 つの相補的な組み合わせ数の結果は同一になります。
![]()
組み合わせ数のこの特性は、対称恒等とも呼ばれます。
たとえば、6-4=2 であるため、6 オーバー 4 は 6 オーバー 2 と同じ結果になります。
![]()
![]()
- 同じ分子で連続する次数を持つ 2 つの組み合わせ数の合計は、その分子が加算の分子に 1 を加えたものに等しく、次数が加算の次数の最大値に対応する別の組合せ数と等しくなります。つまり、次の条件が常に満たされます。
![]()
例えば:
![]()
この性質はパスカル則とも呼ばれます。
一方、この公式を逆に適用して、組み合わせ数を 2 つの単純な組み合わせ数に分解することもできます。
![]()
たとえば、8 対 4 の組み合わせは、7 対 3 と 7 対 4 を足したものに等しくなります。
![]()
- 1 より大きい正の数値は、その数値自体と等しくなります。
![]()
この性質がある理由は、数値の階乗が、前の数値の階乗にその数値自体を乗算したものに等しいためです。
![]()
このタイプの組み合わせ数値の例:
![]()
- 0 より大きい正の数は 1 と等しくなります。
![]()
実際、このような組み合わせ数の分数の分母は常に分数の分子と等しくなります。
![]()
次のような組み合わせ数値の例:
![]()
- それ自体の各数字は 1 に等しくなります。
![]()
デモは次のとおりです。
![]()
次のような組み合わせ数値の例:
![]()
電卓を使って組み合わせ数を計算する方法
これまで、多かれ少なかれ単純な数値の組み合わせ数を見つける方法を見てきましたが、非常に大量の数値を操作する必要がある場合は、計算機を使用して組み合わせ数を決定する方が良いでしょう。次に、計算機に組み合わせ数値を入力する方法を見てみましょう。
したがって、電卓で組み合わせ数値を計算するために使用されるキーはnCr キーです。組み合わせ数の値を決定するには、まず組み合わせ数の分子を入力し、次に nCr キーを押し、次に組み合わせ数の順序を入力し、最後に等号キーを押す必要があります。
![]()
CASIO の関数電卓では、モデルに応じて、通常、nCr キーに専用のボタンがあるか、除算ボタンの上にあります。
たとえば、6 上の 10 の組み合わせが何であるかを知りたい場合は、次の手順を実行する必要があります。
![]()
組み合わせ数の応用
ここまで読んだ人は、おそらく、組み合わせ数を完璧に解く方法をすでに知っているでしょう。しかし…組み合わせ数は何に使われるのでしょうか?さて、このタイプの非常に特殊な操作がもたらす利点をすべて見ていきます。
組み合わせ論
ページの上部で見たように、組み合わせ数の結果
![]()
可能なグループの数を表します
![]()
の集合から形成できる要素
![]()
アイテム。
したがって、一部の組み合わせ問題は、組み合わせ数 (または二項係数) を使用して解決できます。例を使用してこれを行う方法を見てみましょう。
- 30 人の生徒のクラスで、特定のタスクを実行するために 4 人の生徒のグループを選択したいとします。形成できるさまざまなグループの合計数は何ですか?
この場合、生徒の順序は重要ではなく、グループ内で同じ生徒が 2 回繰り返されることはなく、すべての生徒がグループに入るわけではありません。したがって、組み合わせ数公式を使用して、グループを形成できる方法が何通りあるかを決定できます。
これを行うには、学生の総数を分子として、グループを形成する学生の数を順序として使用して、組み合わせ数を計算する必要があります。
![]()
したがって、可能な組み合わせの総数は 27,405 グループになります。
ニュートンの二項式
組み合わせ数のもう 1 つの応用は、ニュートンの二項式です。ニュートンの二項式は、整数に累乗された 2 つの項で構成される多項式です。つまり、ニュートンの二項式は、次の代数式に応答する多項式です。
![]()
明らかに、二項式が二乗されている場合、これは注目すべき恒等式であることを意味するため、対応する式を使用して簡単に計算できます。一方、二項式を大きな数にすると、計算が非常に困難になります。ニュートンの二項定理によれば、この種の多項式は組み合わせ数から非常に簡単に計算できます。
次のリンクをクリックして、 ニュートンの二項公式とその計算方法を確認してください。さらに、例を見て、段階的に解決される演習で練習することができます。そして最後に、この定理の興味深い歴史を知ることができます。
タルターリア (またはパスカル) の三角形
この記事全体を通して見てきたように、大きな数値の二項係数を手動で計算することは、手間がかかり、複雑になる可能性があります。
一方、パスカルの三角形とも呼ばれるタルターリアの三角形では、すべての組み合わせ数は記憶規則を使用して簡単に決定できます。これは計算時間を大幅に節約できるため、論理的に非常に便利です。
これを行う正確な方法については、 Tartaglia の三角形の説明を参照してください。このリンクされたページでは、この神秘的な三角形が何であるか、何に使われるか (驚くべき用途があります) 😮、そしてその起源が何であるか (すでに 1000 年以上前に使用されていました) がわかります。
組み合わせ数の練習問題を解決しました
説明した概念を練習して完全に理解できるように、組み合わせ数について段階的に解決するいくつかの演習を用意しています。
演習 1
(電卓を使用せずに) 9 x 5 の組み合わせ数を見つけます。
5 のうち 9 の組み合わせ数値を求めるには、次の階乗公式を適用するだけです。
![]()
演習 2
次の 2 つの組み合わせ数の合計の結果は何ですか? (電卓なし)
![]()
組み合わせ数の性質から、問題の合計は次の組み合わせ数に等しいことがわかります。
![]()
したがって、7 のうち 11 の組み合わせ数を計算するだけで十分です。
![]()
演習 3
次の組み合わせ数値が等しいかどうかを判断します。
![]()
3 つの組み合わせ数値の結果を求めるのに電卓を使用する必要はありませんが、組み合わせ数値の特性のおかげで簡単に求めることができます。
まず、0 より大きい任意の数値の組み合わせは 1 になります。したがって、次のようになります。
![]()
一方、1 より大きい数値はその数値そのものと等しくなります。まだ:
![]()
そして最後に、同じ数値を 2 回繰り返して形成される組み合わせ数値は 1 と同等です。つまり、次のようになります。
![]()
結論として、問題の最初と 3 番目の組み合わせ数は等しいですが、中央の組み合わせ数とは異なります。
![]()